Решения головоломок 16-30

16. Для упрощения задачи отложим пока в сторону все 7 двойных косточек: 0-0, 1-1, 2-2 и т. д. Останется 21 косточка, на которых каждое число очков повторяется 6 раз. Например, 4 очка (на одном поле) имеется на следующих 6 косточках:

4-0; 4-1; 4-2; 4-3; 4-5; 4-6.

Итак, каждое число очков повторяется, мы видим, четное число раз. Ясно, что косточки такого набора можно приставлять одну к другой равными числами очков до исчерпания всего набора. А когда это сделано, когда наши 21 косточка вытянуты в непрерывную цепь, тогда между стыками 0-0, 1-1, 2-2 и т. д. вдвигаем отложенные 7 двойняшек. После этого все 28 косточек домино оказываются вытянутыми, с соблюдением правил игры, в одну цепь.

17. Легко показать, что цепь из 28 костей домино должна кончаться тем же числом очков, каким она начинается. В самом деле: если бы было не так, то числа очков, оказавшиеся на концах цепи, повторялись бы нечетное число раз (внутри цепи числа очков лежат ведь парами); мы знаем, однако, что в полном наборе костей домино каждое число очков повторяется 8 раз, т. е. четное число раз. Следовательно, сделанное нами допущение о неодинаковом числе очков на концах цепи - неправильно: числа очков должны быть одинаковы. (Рассуждения такого рода, как это, в математике называются "доказательствами от противного".)

Между прочим, из только что докапанного свойства цепи вытекает следующее любопытное следствие: цепь из 28 косточек всегда можно сомкнуть концами и получить кольцо. Полный набор костей домино может быть, значит, выложен, с соблюдением правил игры, не только в цепь со свободными концами, но также и в замкнутое кольцо.

Читателя может заинтересовать вопрос: сколькими различными способами выполняется такая цепь или кольцо? Не входя в утомительные подробности расчета, скажем здесь, что число различных способов составления 28-косточковой цепи (или кольца) огромно: свыше 7 триллионов. Вот точное число:

7 959 229 931 520

(оно представляет собою произведение следующих множителей: 2¹³×38×5×7×4231).

18. Решение этой головоломки вытекает из только что сказанного. 28 косточек домино, мы знаем, всегда выкладываются в сомкнутое кольцо; следовательно, если из этого кольца вынуть одну косточку, то

1. остальные 27 косточек составят непрерывную цепь с разомкнутыми концами;
2. концевые числа очков этой цепи будут те, которые имеются на вынутой косточке.

Спрятав одну кость домино, мы можем поэтому заранее сказать, какие числа очков будут на концах цепи, составленной из прочих костей.

19. Сумма очков всех сторон искомого квадрата должна равняться 44x4=176, т. е. на 8 больше, чем сумма очков на косточках полного набора домино (168). Происходит это, конечно, оттого, что числа очков, занимающих вершины квадрата, считаются дважды. Сказанным определяется, какова должна быть сумма очков на вершинах квадрата: 8. Это несколько облегчает поиски требуемого расположения, хотя нахождение его все же довольно хлопотливо. Решение показано на рис. 15.

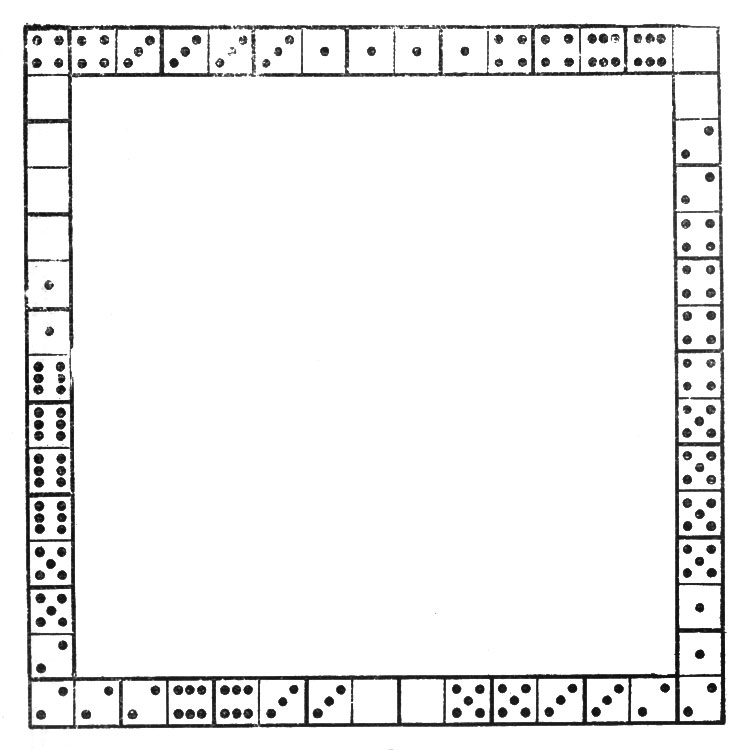
Рис. 15. Решение 19 задачи

20. Приводим два решения этой задачи из числа многих возможных. В первом решении (рис. 16) имеем:

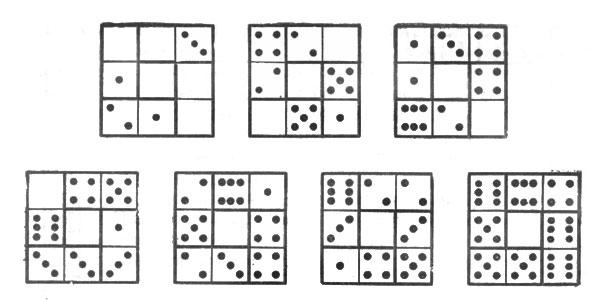
Рис. 16. Первое решение

 1 квадрат с суммою 3,  2 квадрата с суммою 9, 
 1 квадрат с суммою 6,  1 квадрат с суммою 10, 
 1 квадрат с суммою 8,  1 квадрат с суммою 16.

Во втором решении (рис. 17):

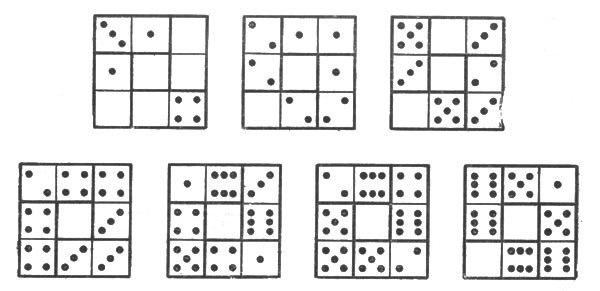
Рис. 17. Второе решение

 2 квадрата с суммою 4,  2 с суммою 10, 
 1 квадрат с суммою 8,   2 с суммою 12.

21. На рис. 18 дан образчик магического квадрата с суммою очков в ряду 18.

Рис. 18. Магический квадрат с суммою очков в ряду 18

22. Вот в виде примера две прогрессии с разностью 2:

• а) 0-0; 0-2; 0-4; 0-6; 4-4 (или 3-5); 5-5 (или 4-6).
• б) 0-1; 0-3 (или 1-2); 0-5 (или 2-3): 1-6 (или 3-4); 3-6 (или 4-5); 5-6.

Всех 6-косточковых прогрессий можно составить 23. Начальные косточки их следующие:

• а) для прогрессий с разностью 1:

   0-0 1-1 2-1 2-2 3-2 
  
   0-1 2-0 3-0 3-1 2-4 
  
   1-0 0-3 0-4 1-4 3-5 
  
   0-2 1-2 1-3 2-3 3-4 
  

• б) для прогрессий с разностью 2:

  0-0; 0-2; 0-1. 
  

23. Расположение задачи может быть получено из начального положения следующими 44 ходами:

 14, 11, 12,  8,  7,  6,  10,  12,  8,  7, 

  4,  3,  6,  4,  7, 14,  11,  15, 13,  9, 

 12,  8,  4, 10,  8,  4,  14,  11, 15, 13, 

 9,  12,  4,  8,  5,  4,   8,   9, 13, 14, 

 10,  6,  2,  1. 

24. Расположение задачи достигается следующими 39 ходами:

 14, 15, 10, 6, 7, 11, 15, 10, 13,  9, 

  5,  1,  2, 3, 4,  8, 12, 15, 10, 13, 

  9,  5,  1, 2, 3,  4,  8, 12, 15, 14, 

 13,  9,  5, 1, 2,  3,  4,  8, 12. 

25. Магический квадрат с суммою 30 получается после ряда ходов:

 12,  8,  4, 3,  2,  6, 10,  9, 13, 15, 

 14, 12,  8, 4,  7, 10,  9, 14, 12,  8, 

  4,  7, 10, 9,  6,  2,  3, 10,  9,  6, 

  5,  1,  2, 3,  6,  5,  3,  2,  1, 13, 

 14,  3,  2, 1, 13, 14,  3, 12, 15,  3. 

26. Даже опытный игрок скажет, вероятно, что при указанных условиях пройти ворота легче, чем крокировать: ведь ворота вдвое шире шара. Однако такое представление ошибочно: ворота, конечно, шире, нежели шар, но свободный проход для шара через ворота вдвое уже, чем мишень для крокировки.

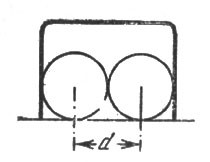
Рис. 19. Центр шара не должен приближаться к проволоке ворот меньше чем на величину радиуса

Взгляните на рис. 19, и сказанное станет вам ясно. Центр шара не должен приближаться к проволоке ворот меньше чем на величину радиуса, иначе шар заденет проволоку. Значит, для центра шара останется мишень на два радиуса меньше ширины ворот. Легко видеть, что в условиях нашей задачи ширина мишени при прохождении ворот с наилучшей позиции равна диаметру шара.

Посмотрим теперь, как велика ширина мишени для центра движущегося шара при крокировке. Очевидно, что если центр крокирующего приблизится к центру крокируемого меньше чем на радиус шара, удар обеспечен. Значит, ширина мишени в этом случае, как видно из рис. 20, равна двум диаметрам шара.

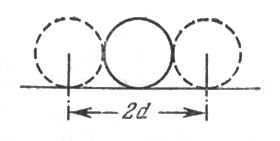
Рис. 20. Ширина мишени в этом случае равна двум диаметрам шара

Итак, вопреки мнению игроков, при данных условиях вдвое легче попасть в шар, нежели свободно пройти ворота с самой лучшей позиции.

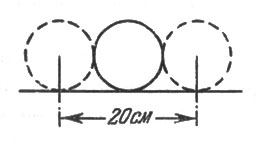
Рис. 21. Ширина цели при крокировке равна двум диаметрам шара, т. е. 20 см

27. После только что сказанного эта задача не требует долгих разъяснений. Легко видеть (рис. 21), что ширина цели при крокировке равна двум диаметрам шара, т. е. 20 см; ширина же мишени при нацеливании в столбик равна сумме диаметра шара и столбика, т. е. 16 см (рис. 22). Значит, крокировать легче, чем заколоться, в

 20:16= 1 1/4 раза,

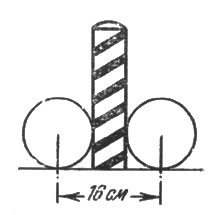
Рис. 22. Ширина же мишени при нацеливании в столбик равна сумме диаметра шара и столбика, т. е. 16 см всего на 25%. Игроки же обычно сильно преувеличивают шансы крокировки по сравнению с попаданием в столбик.

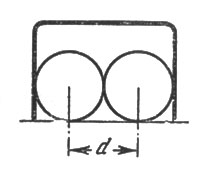
Рис. 23

28. Иной игрок рассудит так: раз ворота вдвое шире чем шар, а столбик вдвое уже шара, то для свободного прохода ворот мишень вчетверо шире, чем для попадания в столбик. Наученный предыдущими задачами, читатель наш подобной ошибки не сделает. Он сообразит, что для прицела в столбик мишень в 1 1/2 раза шире, чем для прохода ворот с наилучшей позиции. Это ясно из рассмотрения рис. 23 и 24.

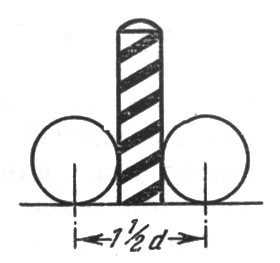
Рис. 24

(Если бы ворота были не прямоугольные, а выгнутые дугой, проход для шара был бы еще уже - как легко сообразить из рассмотрения рис. 25.)

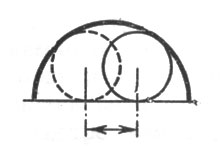
Рис. 25. Если бы ворота были не прямоугольные, а выгнутые дугой, проход для шара был бы еще уже

29. Из рис. 26 и 27 видно, что промежуток а, остающийся для прохода центра шара, довольно тесен при указанных в задаче условиях. Знакомые с геометрией знают, что сторона АВ квадрата меньше его диагонали АС примерно в 1,4 раза.

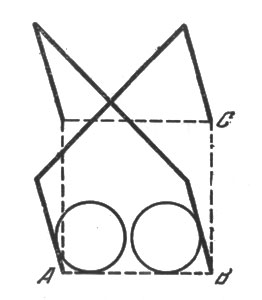
Рис. 26

Если ширина ворот 3d (где d - диаметр шара), то АВ равно

3d:l,4≈2,1d

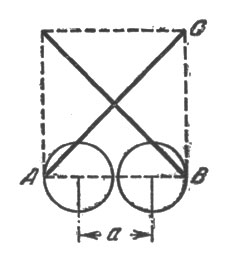
Рис. 27

Промежуток же а, который является мишенью для центра шара, проходящего мышеловку с наилучшей позиции, - еще уже. Он на целый диаметр меньше, т. е. равен:

2,1d - d = 1,1d.

Между тем мишень для центра крокирующего шара равна, как мы знаем, 2d. Следовательно, крокировать почти вдвое легче при данных условиях, чем пройти мышеловку.

30. Мышеловка становится совершенно непроходимой в том случае, когда ширина ворот превышает диаметр шара менее чем в 1,4 раpа. Это вытекает ив объяснения, данного в предыдущей задаче. Если ворота дугообразные, условия прохождения еще более ухудшаются.