Игра в 15, или такен

Общеизвестная коробочка с 15 нумерованными квадратными шашками имеет любопытную историю, о которой мало кто из игроков подозревает. Расскажем о ней словами немецкого исследователя игр, математика В. Аренса.

"Около полувека назад - в конце 70-х годов - вынырнула в Соединенных Штатах "игра в 15"; она быстро распространилась и, благодаря несчетному числу игроков, которых она заполонила, превратилась в настоящее общественное бедствие.

"То же наблюдалось по эту сторону океана, в Европе. Здесь можно было даже в конках видеть в руках пассажиров коробочки с 15 шашками. В конторах и магазинах хозяева приходили в отчаяние от увлечения своих служащих и вынуждены были воспретить им игру в часы занятий и торговли. Содержатели увеселительных заведений ловко использовали эту манию и устраивали большие игорные турниры.

Игра проникла даже в торжественные залы германского рейхстага. "Как сейчас вижу в рейхстаге седовласых людей, сосредоточенно рассматривающих в своих руках квадратную коробочку", - вспоминает известный географ и математик Зигмунд Гюнтер, бывший депутатом в годы игорной эпидемии.

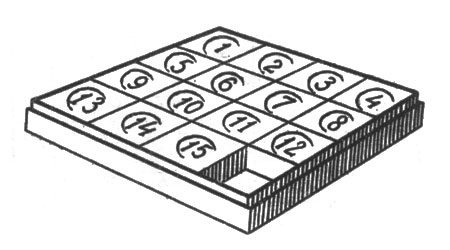
Рис. 9. Игра в 15

"В Париже игра эта нашла себе приют под открытым небом, на бульварах, и быстро распространилась из столицы по всей провинции. "Не было такого уединенного сельского домика, где не гнездился бы этот паук, подстерегая жертву, готовую запутаться в его сетях", - писал один французский автор.

"В 1880 г. игорная лихорадка достигла, по-видимому, своей высшей точки. Но вскоре после этого тиран был повержен и побежден оружием математики. Математическая теория игры обнаружила, что из многочисленных задач, которые могут быть предложены, разрешима только половина; другая не разрешима никакими ухищрениями.

"Стало ясно, почему иные задачи не поддавались самым упорным усилиям, и почему устроители турниров отваживались назначать огромные премии за разрешения задач. В этом отношении всех превзошел изобретатель игры, предложивший издателю нью-йоркской газеты для воскресного приложения неразрешимую задачу с премией в 1000 долларов за ее разрешение; так как издатель колебался, то изобретатель выразил полную готовность внести названную сумму из собственного кармана. Имя изобретателя Самуэль (Сэм) Лойд. Он приобрел широкую известность как составитель остроумных задач и множества головоломок. Любопытно, что получить в Америке патент на придуманную игру ему не удалось. Согласно инструкции, он должен был представить "рабочую модель" для исполнения пробной партии; он предложил чиновнику патентного бюро задачу, и когда последний осведомился, разрешима ли она, изобретатель должен был ответить: "Нет, это математически невозможно". "В таком случае, - последовало возражение, - не может быть и рабочей модели, а без модели нет и патента". Лойд удовлетворился этой резолюцией, - но, вероятно, был бы более настойчив, если бы предвидел неслыханный успех своего изобретения"^*.

^* (Этот эпизод использован Марком Твэном в его романе "Американский претендент".)

Приведем собственный рассказ изобретателя игры о некоторых фактах из ее истории:

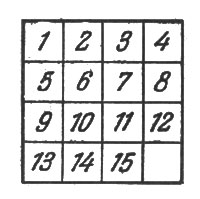
Рис. 10. Игра в 15

"Давнишние обитатели царства смекалки, - пишет Лойд, - помнят, как в начале 70-х годов я заставил весь мир ломать голову над коробкой с подвижными шашками, получившей известность под именем "игры в 15" (рис. 10). Пятнадцать шашек были размещены в квадратной коробочке в правильном порядке, и только шашки 14 и 15 были переставлены, как показано на прилагаемой иллюстрации (рис. 11). Задача состояла в том, чтобы, последовательно передвигая шашки, привести их в нормальное положение, причем, однако, порядок шашек 14 и 15 должен быть исправлен.

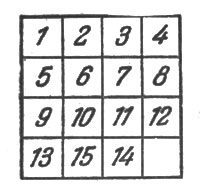
Рис. 11. Пятнадцать шашек были размещены в квадратной коробочке в правильном порядке, и только шашки 14 и 15 были переставлены

"Премия в 1000 долларов, предложенная за первое правильное решение этой задачи, никем не была заслужена, хотя все без устали решали эту задачу. Рассказывали забавные истории о торговцах, забывавших из-за этого открывать свои магазины, о почтенных чиновниках, целые ночи напролет простаивавших под уличным фонарем, отыскивая путь к решению. Никто не желал отказаться от поисков решения, так как все чувствовали уверенность в ожидающем их успехе. Штурманы, говорят, из-за игры сажали на мель свои суда, машинисты проводили поезда мимо станций; фермеры забрасывали свои плуги".

Познакомим читателя с начатками теории этой игры. В полном виде она очень сложна и тесно примыкает к одному из отделов высшей алгебры ("теория определителей"). Мы ограничимся лишь некоторыми соображениями, изложенными В. Аренсом.

"Задача игры состоит обыкновенно в том, чтобы посредством последовательных передвижений, допускаемых наличием свободного поля, перевести любое начальное расположение 15 шашек в нормальное, т. е. в такое, при котором шашки идут в порядке своих чисел: в верхнем левом углу 1, направо - 2, затем 3, потом в верхнем правом углу 4; в следующем ряду слева направо: 5, 6, 7, 8 и т. д. Такое нормальное конечное расположение мы даем здесь на рис. 10.

"Вообразите теперь расположение, при котором 15 шашек размещены в пестром беспорядке. Рядом передвижений всегда можно привести шашку 1 на место, занимаемое ею на рисунке.

"Точно так же возможно, не трогая шашки 1, привести шашку 2 на соседнее место вправо. Затем, не трогая шашек 1 и 2, можно поместить шашки 3 и 4 на их нормальные места: если они случайно не находятся в двух последних вертикальных рядах, то легко привести их в эту область и затем рядом передвижений достичь желаемого результата. Теперь верхняя строка 1, 2, 3, 4 приведена в порядок, и при дальнейших манипуляциях с шашками мы трогать этого ряда не будем. Таким же путем стараемся мы привести в порядок и вторую строку: 5, 6, 7, 8; легко убедиться, что это всегда достижимо. Далее, на пространстве двух последних рядов необходимо привести в нормальное положение шашки 9 и 13; это тоже всегда возможно. Из всех приведенных в порядок шашек 1, 2, 3, 4, 5, 6, 7, 8, 9 и 13 в дальнейшем ни одной не перемещают; остается небольшой участок в шесть полей, в котором одно свободно, а пять остальных заняты шашками 10, 11, 12, 14, 15 в произвольном порядке. В пределах этого шестиместного участка всегда можно привести на нормальные места шашки 10, 11, 12. Когда это достигнуто, то в последнем ряду шашки 14 и 15 окажутся размещенными либо в нормальном порядке, либо в обратном (рис. 11). Таким путем, который читатели легко могут проверить на деле, мы приходим к следующему результату.

"Любое начальное положение может быть приведено к расположению либо рис. 10 (положение I), либо рис. 11 (положение II).

"Если некоторое расположение, которое для краткости обозначим буквою S, может быть преобразовано в положение I, то, очевидно, возможно и обратное - перевести положение I в положение S. Ведь все ходы шашек обратимы: если, например, в схеме I мы можем шашку 12 поместить на свободное поле, то можно ход этот тотчас взять обратно противоположными движениями.

"Итак, мы имеем две такие серии расположений, что положения одной серии могут быть переведены в нормальное I, а другой серии - в положение II. И наоборот, из нормального расположения можно получить любое положение первой серии, а из расположения II - любое положение второй серии. Наконец, два любых расположения, принадлежащих к одной и той же серии, могут быть переводимы друг в друга.

"Нельзя ли идти дальше и объединить эти два расположения - I и II? Можно строго доказать (не станем входить в подробности), что положения эти не превращаются одно в другое никаким числом ходов. Поэтому все огромное число размещений шашек распадается на две разобщенные серии:

1. на те, которые могут быть переведены в нормальное I: это - положения разрешимые,
2. на те, которые могут быть переведены в положение II и, следовательно, ни при каких обстоятельствах не переводятся в нормальное расположение: это - положения, за разрешение которых назначались огромные премии.

Рис. 12. '...о почтенных чиновниках, целые ночи напролет простаивавших под фонарем...'

"Как узнать, принадлежит ли заданное расположение к первой или ко второй серии? Пример разъяснит это.

"Рассмотрим такое расположение.

"Первый ряд шашек в порядке, как и второй, за исключением последней шашки (9). Эта шашка занимает место, которое в нормальном расположении принадлежит 8. Шашка 9 стоит, значит, ранее шашки 8: такое упреждение нормального порядка называют "беспорядком". О шашке 9 мы скажем: здесь имеет место 1 беспорядок. Рассматривая дальнейшие шашки, обнаруживаем "упреждение" для шашки 14; она поставлена на три места (шашек 12, 13. 11) ранее своего нормального положения; здесь у нас 3 беспорядка (14 ранее 12; 14 ранее 13; 14 ранее 11). Всего мы насчитали уже 1+3=4 беспорядка. Далее, шашка 12 помещена ранее шашки 11, и точно так же шашка 13 ранее шашки 11. Это дает еще 2 беспорядка. Итого имеем 6 беспорядков. Подобным образом для каждого расположения устанавливают общее число беспорядков, освободив предварительно последнее место в правом нижнем углу. Если общее число беспорядков, как в рассмотренном случае, четное, то заданное расположение может быть приведено к нормальному конечному; другими словами, оно принадлежит к разрешимым. Если же число беспорядков нечетное, то расположение принадлежит ко второй серии, т. е. к неразрешимым (нуль беспорядков принимается за четное число их).

"Благодаря ясности, внесенной в эту игру математикой, прежняя лихорадочная страстность в увлечении сейчас совершенно немыслима. Математика создала исчерпывающую теорию игры, теорию, не оставляющую ни одного сомнительного пункта. Исход игры зависит не от каких-либо случайностей, не от находчивости, как в других играх, а от чисто математических факторов, предопределяющих его с безусловной достоверностью". Обратимся теперь к головоломкам в этой области. Вот несколько разрешимых задач, придуманных изобретателем игры:

23. Первая задача Лойда.

Исходя из расположения, показанного на рис. 11, привести шашки в правильный порядок, но со свободным полем в левом верхнем углу (рис. 13).

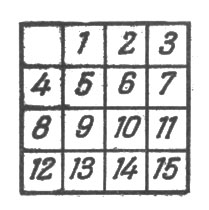
Рис. 13. Шашки в правильном порядке, но со свободным полем в левом верхнем углу

24. Вторая задача Лойда.

Исходя из расположения рис. 11 поверните коробку на четверть оборота и передвигайте шашки до тех пор, пока они не примут расположения рис. 14.

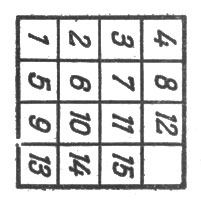
Рис. 14. Вторая задача Лойда

25. Третья задача Лойда.

Передвигая шашки согласно правилам игры из расположения рис. И, превратите коробку в "магический квадрат", а именно, разместите шашки так, чтобы сумма чисел была во всех направлениях равна 30.