Глава вторая. Математика в играх

Домино

16. Цепь из 28 костей.

Почему 28 костей домино можно выложить с соблюдением правил игры в одну непрерывную цепь?

17. Начало и конец цепи.

Когда 28 костей домино выложены в цепь, на одном ее конце оказалось 5 очков.

Сколько очков на другом конце?

18. Фокус с домино.

Ваш товарищ берет одну из костей домино и предлагает вам из остальных 27 составить непрерывную цепь, утверждая, что это всегда возможно, какая бы кость ни была взята. Сам же он удаляется в соседнюю комнату, чтобы не видеть вашей цепи.

Вы приступаете к работе и убеждаетесь, что товарищ ваш прав: 27 костей выложились в одну цепь. Еще удивительнее то, что товарищ, оставаясь в соседней комнате и не видя вашей цепи, объявляет оттуда, какие числа очков на ее концах.

Как может он это знать? И почему он уверен, что из всяких 27 костей домино составится непрерывная цепь?

19. Рамка.

Рис. 5 изображает квадратную рамку, выложенную из костей домино с соблюдением правил игры. Стороны рамки равны по длине, но не одинаковы по сумме очков: верхний и левый ряды заключают по 44 очка, остальные же два ряда - 59 и 32.

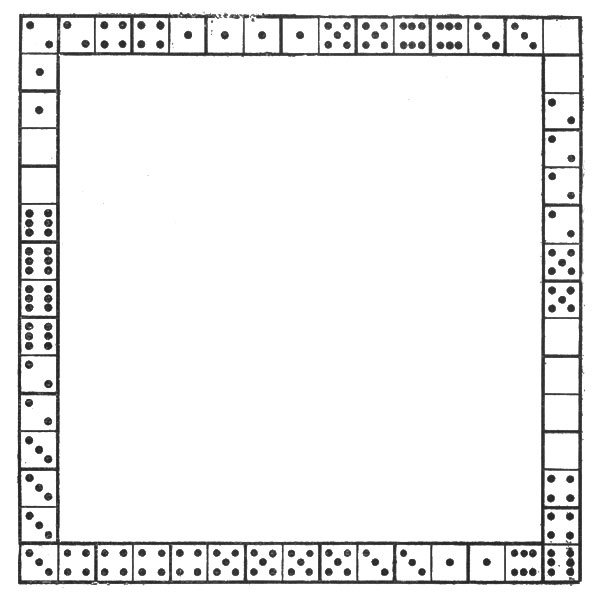
Рис. 5. Квадратная рамка

Можете ли вы выложить такую квадратную рамку, все стороны которой заключали бы одинаковую сумму очков - именно 44?

20. Семь квадратов.

Четыре кости домино можно выбрать так, чтобы из них составился квадратик с равной суммой очков на каждой стороне. (Образчик вы видите на рис. 6: сложив очки на каждой стороне квадратика, во всех случаях получите 11.)

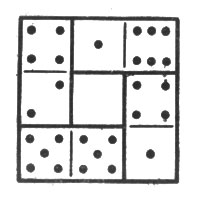
Рис. 6. Сложив очки на каждой стороне квадратика, во всех случаях получите 11

Можете ли вы из полного набора домино составить одновременно семь таких квадратов? Не требуется, чтобы сумма очков на одной стороне была у всех квадратов одна и та же; надо лишь, чтобы каждый квадрат имел на своих четырех сторонах одинаковую сумму очков.

21. Магические квадраты из домино.

На рис. 7 показан квадрат из 18 косточек домино, замечательный тем, что сумма очков любого его ряда - продольного, поперечного или диагонального - одна и та же: 13. Подобные квадраты издавна называются "магическими".

Рис. 7. Квадрат из 18 косточек домино, замечательный тем, что сумма очков любого его ряда - продольного, поперечного или диагонального - одна и та же: 13

Вам предлагается составить несколько таких же 18-косточковых магических квадратов, но с другой суммой очков в ряду. 13 - наименьшая сумма в рядах магического квадрата, составленного из 18 костей. Наибольшая сумма - 23.

22. Прогрессия из домино.

Вы видите на рис. 8 шесть косточек домино, выложенных по правилам игры и отличающихся тем, что число очков на косточках (на двух половинах каждой косточки) возрастает на 1. Ряд начинается с 4 и состоит из следующих чисел очков:

4; 5; 6; 7; 8; 9.

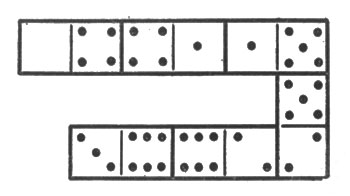
Рис. 8. Шесть косточек домино, выложенных по правилам игры и отличающихся тем, что число очков на косточках (на двух половинах каждой косточки) возрастает на 1

Такой ряд чисел, которые возрастают (или убывают) на одну и ту же величину, называется "арифметической прогрессией". В нашем ряду каждое число больше предыдущего на 1; но в прогрессии может быть и любая другая "разность".

Задача состоит в том, чтобы составить еще несколько 6-косточковых прогрессий.