
История одной игры. Вильгельма Аренса

История одной игры
* (Доктор Вильгельм Аренc широко известен своими исследованиями в области математических игр. Главный его труд "Математические развлечения и игры", в двух больших томах, разрабатывает эту область с исчерпывающей полнотой и строгой научностью. Ему принадлежат также следующие сочинения: "Математические развлечения" (более краткое и общепонятное, чем упомянутое выше; есть русский перевод), "Старое и новое из области занимательной математики", "Забава и дело в математике", "Анекдоты о математиках". - Предлагаемый здесь очерк опубликован в 1924 г. в одном математическом сборнике и появляется на русском языке впервые. Ред.)
I
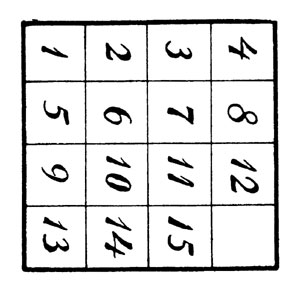
Около полувека назад, - в конце 70-х годов - вынырнула в Соединенных Штатах одна игра, "игра в 15"; она быстро распространилась по всему цивилизованному миру и, благодаря несчетному числу усердных игроков, которых она заполонила, превратилась в настоящее общественное бедствие, в истинный бич человечества. Заглавный рисунок, заимствуемый из одного американского сочинения, изображает эту игру: коробку с 15 шашками, перенумерованными от 1 до 15, и одним свободным полем. Перед ящиком мы видим жертву игорной страсти, одного из многочисленных одержимых этой манией; в разгар полевой работы, он, поддавшись внезапно приступу игорной лихорадки, кинулся на колени перед демоном, которому поклонялся. Растерянность видна во всей его фигуре, во всех его чертах; лицо искажено отчаянием; правая рука нервно сжата в кулак; левая рука и наморщенный лоб охвачены судорогой. Кожа головы, после ряда усилий, скинула шляпу; волосы дико растрепаны. Забыт труд, покинута лошадь и плуг; на нем уселась пара птиц; даже заяц, обычно столь пугливый, сознает, что этот потерянный для мира маниак, всецело погруженный в 15 шашек своей коробки, не представляет для него ни малейшей опасности.
То же наблюдалось и по эту сторону океана, в Европе. Здесь можно было даже в конках видеть коробочки с 15 шашками в суетливых руках, передвигавших шашки по разным направлениям. В конторах и торговых помещениях хозяева приходили в отчаяние от игорного увлечения своих служащих и вынуждены были строгими угрозами воспретить им игру в часы занятий и торговли. Оборотливые содержатели увеселительных заведений ловко использовали эту манию и устраивали у себя большие игорные турниры, Так описывает гамбургский математик Г. Шуберт зарождение игорной эпидемии в его городе.
Даже в торжественные залы германского рейхстага сумел проникнуть змий-искуситель. "Эта вещица поистине околдовывала. Как сейчас вижу я в рейхстаге седовласых людей, сосредоточенно рассматривающих в своих руках квадратную коробочку", - рассказывал, спустя десятилетия, известный географ и математик Зигмунд Гюнтер, бывший в годы игорной эпидемии депутатом рейхстага.
В Париже опасная игра нашла себе приют под открытым небом, на бульварах, и быстро распространилась из столицы по всей провинции*. Вскоре - говорят французские источники - не было в провинции ни одного уединенного сельского домика, где не угнездился бы этот паук, подстерегая жертву, готовую запутаться в его сетях. Настоящий бич человечества, - вот какой рисуется эта игра одному французскому автору: - "бедствие, более страшное, чем табак и алкоголь", - восклицает он в комическом отчаянии.
* (Во Франции игра эта более известна под названием такен. Ред.)
В 1880 г. игорная лихорадка достигла, по-видимому, своей высшей точки. Вся пестрая, разноязычная литература, порожденная этой игрой, относится к немногим годам между 1879-м и 1883.
Вскоре после этого демон, тиранивший стольких людей, был повержен и побежден. Математика - вот его победительница, и победа не была для нее особенно трудной, между тем как "демон алкоголя и табака" никогда, конечно, не будет следовать за ее триумфальной колесницей, сколько бы славы ни сулила победа над ним.
Когда демон был оружием математики повержен во-прах, источник мучений столь многих и многих стал ясен для всех. Математическая теория игры обнаружила, что из многочисленных задач, которые могут быть предложены, только половина разрешима, между тем как другая не разрешима никакими ухищрениями.
Стало ясно, почему иные задачи не поддавались самым упорным усилиям; стало ясно, почему устроители турниров отваживались назначать огромные премии за разрешение некоторых задач, и ни один из многочисленных соревнователей не смог овладеть ими.
В этом отношении всех превзошел сам изобретатель игры, предложивший издателю нью-йоркской газеты для воскресного прибавления неразрешимую задачу с премией в 1000 долларов за ее разрешение; и так как издатель колебался, то изобретатель выразил полную готовность внести названную сумму из собственного кармана.

Самуэль Лойд - популярнейший и плодовитейший в мире изобретатель головоломных задач и развлечений. Он и в настоящее время продолжает вести во многих американских журналах отдел головоломок, получая от решающих десятки тысяч ответов ежемесячно
Мы до сих пор не назвали имени изобретателя: Самуэль (Сам) Лойд. Он родился в городе Филадельфии. В шахматных кругах он приобрел широкую известность как составитель остроумных задач; кроме того, им придумано множество иных головоломок. Мы воспроизводим здесь портрет этого изобретательного человека. Любопытно, что ему не удалось получить в Америке патента на придуманную им игру. Хотя Лойд не мог предусмотреть чудовищного успеха своего изобретения и совершенно не ожидал его, он подал заявление о патенте. Согласно инструкции, он должен был представить "рабочую модель" для исполнения пробной партии; он предложил чиновнику патентного бюро неразрешимую задачу (вероятно, ту, которая изображена на рис. стр. 91), и когда последний осведомился, разрешима ли она, изобретатель должен был ответить: "Нет, это математически невозможно". - "В таком случае, - последовало возражение, - раз задача не разрешима, то не может быть и рабочей модели, а без модели нет и патента". Странным образом Лойд удовлетворился этой мнимой логикой и этой удивительной резолюцией, - но, вероятно, был бы более настойчив, если бы хоть отчасти предвидел неслыханный успех своего изобретения.
II
Изобретенная в Америке, игра эта получила там и первую свою математическую теорию - в трудах американских математиков Вулсей Джонсона и Вильяма Сторн. Впрочем, независимо от них и вскоре вслед за ними развил основания этой теории также ряд других математиков в различных странах Европы.
Сейчас мы набросаем очерк этой теории, по крайней мере, в главных ее чертах. Задача игры состоит обыкновенно в том, чтобы посредством последовательных передвижений, допускаемых наличием одного свободного поля, перевести любое начальное расположение 15 шашек в нормальное, т. е. в такое, при котором шашки идут в порядке своих чисел: в верхнем левом углу 1, направо - 2, затем 3, потом в верхнем правом углу 4; в следующем ряду слева на право: 5, 6, 7, 8, и т. д. Такое нормальное конечное расположение мы даем здесь на чертеже (схема I).
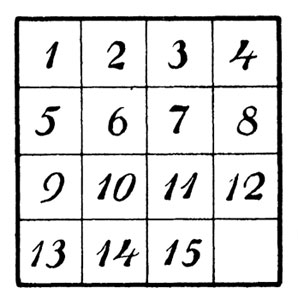
Схема I
Вообразите теперь любое начальное расположение шашек, т. е. такое, при котором 15 шашек размещены в пестром беспорядке. Нетрудно убедиться, что рядом передвижений всегда можно привести шашку № 1 на место, занимаемое ею на чертеже. Точно также возможно, не трогая шашки 1, привести шашку 2 на место рядом с ней, которое она занимает на схеме I. Затем, не трогая шашек 1 и 2, можно поместить шашки 3 и 4 на свои нормальные места: если они случайно не находятся в двух последних вертикальных рядах, то легко привести их в эту область и, затем, рядом передвижений, достичь желаемого результата. Теперь весь, верхний ряд 1, 2, 3, 4 приведен в порядок, и при дальнейших манипуляциях с шашками мы трогать этого ряда не будем. Таким же путем стараемся мы привести в порядок и вторую строку: 5, 6, 7, 8; легко убедиться, что это всегда достижимо. Далее, на пространстве двух последних рядов необходимо привести в нормальное положение (схемы I) шашки 9 и 13: это тоже всегда возможно, в чем нетрудно удостовериться. Из всех приведенных в порядок шашек 1, 2, 3, 4, 5, 6, 7, 8, 9 и 13 ни одной не перемещают в дальнейшем; остается небольшой участок в 6 полей, в котором одно свободно, а пять остальных заняты шашками 10, 11, 12, 14, 15 в произвольном порядке. Легко, однако, убедиться, что в пределах этого шестиместного участка всегда можно привести на нормальные места шашки 10, 11, 12, и когда это достигнуто, то в последнем ряду шашки 14 и 15 окажутся размещенными либо в нормальном порядке либо в обратном (схема II). Таким путем, - который здесь был лишь намечен и который читатели легко могут испытать и проверить на деле, - мы приходим к следующему результату:
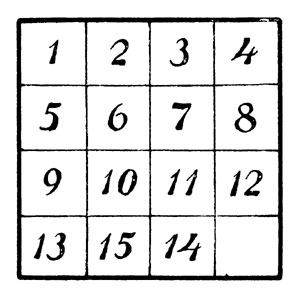
Схема II
Любое начальное положение может быть приведено либо к нормальному схемы I, либо к конечному схемы II.
Это значительно упрощает задачу: все необозримое разнообразие положений шашек сведено к двум типичным схемам I или II, так что приходится иметь дело лишь с этими двумя. Если некоторое расположение, которое для краткости обозначим буквою 5, может быть преобразовано в положение схемы I, то, очевидно, возможно и обратное - перевести положение схемы I в положение S. Ведь все передвижения шашек (все "ходы", как будем говорить кратко) несомненно обратимы: если, например в схеме I мы можем шашку 4 поместить на свободное поле, то можно ход этот тотчас взять обратно противоположным движением. И если расположение переводится в расположение не схемы I, а схемы II, то соответственно этому расположение схемы II может быть переведено в расположение S.
Итак, мы имеем две серии расположений таких, что положения одной серии могут быть все переведены в "нормальное" I, а другой серии - в положение II. И наоборот, мы уже видели, что из "нормального" расположения можно получить любое положение первой серии, а из расположения схемы II - любое положение второй серии. Наконец, два любых расположения, принадлежащие к одной и той же серии, могут быть взаимно переводимы друг в друга: если оба относятся, например, к первой серии, то это значит, что одно из них может быть переведено в положение схемы I, а положение схемы I переводится в другое из данных двух положений; короче - одно данное положение переводимо в другое и наоборот.
Возникает вопрос: нельзя ли идти дальше и объединить эти два типичных расположения - схем I и II? Это было бы возможно, если бы одно из них переводилось каким-нибудь образом в другое. Тогда обе серии расположений естественно слились бы в одну. Сопоставляя друг с другом расположения схем I и II, можно строго доказать (не станем входить здесь в подробности), что положения эти не могут быть превращены одно в другое никаким числом передвижений. Это-огонь и вода. Поэтому все огромное число размещений шашек распадается на две разобщенные серии: 1) на те, которые могут быть переведены в "нормальное" схемы I: это - положения разрешимые; 2) на те, которые могут быть переведены в положение схемы II, и следовательно, ни при каких обстоятельствах не переводятся в "нормальное" конечное расположение: это - положения неразрешенные, те именно, за разрешение которых тщетно назначались огромные премии.
Но как узнать, принадлежит ли заданное расположение к первой или к второй серии? Пример разъяснит это.
Рассмотрим представленное здесь расположение.
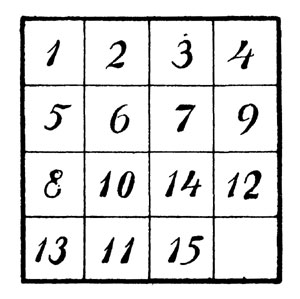
Рассмотрим представленное здесь расположение
Первый ряд шашек в порядке, как и второй, за исключением последней шашки (9). Эта шашка занимает место, которое в "нормальном" расположении принадлежит 8. Шашка 9 стоит, значит, "ранее" шашки 8; такое упреждение нормального порядка будем называть "инверсией". О шашке 9 мы скажем: здесь имеет место "одна инверсия". Рассматривая дальнейшие шашки, обнаруживаем упреждение для шашки 14; она поставлена на три места (шашек 12, 13, 11) ранее своего нормального положения; здесь у нас 3 инверсии (14 ранее 12; 14 ранее 13; 14 ранее 11). Всего мы насчитали уже 1 + 3 = 4 инверсии. Далее шашка 12 помещена ранее шашки 11, и точно так же шашка 13 - ранее шашки 11. Это дает еще 2 инверсии. Итого имеем таким образом 6 инверсий. Подобным образом для каждого заданного расположения устанавливают "общее число инверсий", освободив предварительно последнее место в правом нижнем углу. Если общее число инверсий, как в рассмотренном случае, четное, то заданное расположение может быть приведено к "нормальному" конечному; другими словами, оно принадлежит к разрешимым. Если же число инверсий нечетное, то данное расположение принадлежит ко второй серии, т. е. к неразрешимым.
Из-за недостатка места мы должны отказаться от строгого доказательства всего изложенного. Но можно наметить кратко главные этапы в ходе этого доказательства. Среди ходов будем различать "горизонтальные" и "вертикальные" (смысл этих слов, конечно, ясен). Легко видеть, что всякий "вертикальный" ход изменяет число инверсий либо на 1, либо на 3, т. е. на нечетное число. Чтобы одно положение шашек перевести в какое-либо другое, необходимо сделать h горизонтальных и v вертикальных ходов, причем - если в обоих положениях свободное поле находится в правом нижнем углу, - оба числа, h и v четные. Горизонтальные ходы не могут изменить инверсий, вертикальные же изменяют его каждый раз на нечетное число, т. е. в общем итоге - так как v число четное - на четное число. Вот почему для переводимости двух расположений (в которых пустое поле находится в правом нижнем углу) одного в другое необходимо, чтобы они различались между собою четным числом инверсий. Это условие взаимного перевода является притом не только необходимым, но, очевидно, также и достаточным. - "Нормальное" расположение имеет 0 инверсий, и, следовательно, ему соответствует серия положений с четным числом инверсий (при условии, что свободное поле на одном и том же месте). Расположение II имеет одну инверсию, - ее серия есть серия нечетных инверсий.
Поучительной в этой игре является и ее история. При своем появлении игра вызвала всюду, как мы уже рассказали, сильнейшее, прямо лихорадочное возбуждение и породила настоящую манию игры. С этой лихорадкой удалось справиться только математике. И удалось ей это так полно, что в наши дни подобная страстность в этой игре уже совершенно немыслима. Победа достигнута была благодаря тому, что математика создала исчерпывающую теорию игры, теорию, не оставляющую в ней ни одного сомнительного пункта и превратившую ее в образчик настоящей математической игры. Исход игры зависит здесь не от каких-либо случайностей и даже не от исключительной находчивости, как в других играх, а от чисто математических факторов, предопределяющих исход с безусловной достоверностью*.
* ("Такен (игра в 15), - говорит французский математик Люка - не только весьма интересная игрушка, но также и прибор, помощью которого чрезвычайно легко дать наглядное понятие об одном из важнейших отделов алгебры, а именно о теории определителей, принадлежащей Лейбницу. Поэтому теорию и практические приемы игры в такен можно считать своего рода подготовкой к изучению этой части алгебры". Ред.)
Примечания редактора
Иллюстрация, приведенная в начале этой статьи, помещена в любопытной книге Сама Лойда "Энциклопедия головоломок" (Нью-Йорк, 1914). Это большой том, заключающий 5000 разнообразных задач и развлечений, из которых тысяча иллюстрирована. Рисунок интересующей нас игры сопровождается следующим текстом:
"Давнишние обитатели царства смекалки помнят, как в начале 70-х годов я заставил весь мир ломать голову над коробкой с подвижными шашками, получившей известность под именем "игры в 14-15". Пятнадцать шашек были размещены в квадратной коробочке в правильном порядке, и только шашки 14-я и 15-я были переставлены, как показано на прилагаемой иллюстрации. Задача состояла в том, чтобы последовательно передвигая шашки, привести их в исходное положение, при чем, однако, порядок шашек 14-й и 15-й должен быть исправлен.
Премия в 1000 долларов, предложенная за первое правильное решение этой задачи, никем не была заслужена, хотя тысячи людей уверяли, что выполнили требуемое. Все принялись без устали решать эту задачу. Рассказывали забавные истории о торговцах, забывавших из-за этого открывать свои магазины, о почтенных чиновниках, целые ночи напролет простаивавших под уличным фонарем, отыскивая путь к решению. Непостижимой особенностью игры было то, что никто не желал отказываться от поисков решения, так как все чувствовали уверенность в ожидающем их успехе. Штурмана, говорят, из-за игры садили на мель свои суда, машинисты проводили поезда мимо станций, торговля была деморализована. Фермеры забрасывали свои плуги, и один из таких моментов изображен на прилагаемой иллюстрации.
Вот несколько новых задач, кроме той, которая приведена выше:
- Задача 2-я. Исходя из расположения, показанного на схеме I, привести шашки в правильный порядок, но со свободным полем в левом верхнем углу (см. чертеж).
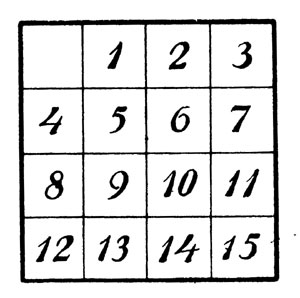
К задаче 2-й - Задача 3-я. Исходя из расположения схемы I, поверните коробку на четверть оборота и передвигайте шашки до тех пор, пока они не примут расположения чертежа.
К задаче 3-й - Задача 4-я. Передвижением шашек превратите коробку в "магический квадрат", а именно, разместите шашки так, чтобы сумма чисел была во всех направлениях равна 30.
Решения
Расположение зад. 2-й может быть получено из начального положения следующими 44 ходами.
14, 11, 12, 8, 7, 6, 10, 12, 8, 7 4, 3, 6, 4, 7, 14, 11, 15, 13, 9 12, 8, 4, 10, 8, 4, 14, 11, 15, 13 9, 12, 4, 8, 5, 4, 8, 9, 13, 14 10, 6, 2, 1.
Расположение зад. 3 достигается следующими 39 ходами:
14, 15, 10, 6, 7, 11, 15, 10, 13, 9 5, 1, 2, 3, 4, 8, 12, 15, 10, 13 9, 5, 1, 2, 3, 4, 8, 12, 15, 14 13, 9, 5, 1, 2, 3, 4, 8, 12.
Магический квадрат с суммою 30 получается после ряда ходов:
12, 8, 4, 3, 2, 6, 10, 9, 13, 15 14, 12, 8, 4, 7, 10, 9, 14, 12, 8 4, 7, 10, 9, 6, 2, 3, 10, 9, 6 5, 1, 2, 3, 6, 5, 3, 2, 1, 13 14, 3, 2, 1, 13, 14, 3, 12, 15, 3.
Приведем замечание немецкого математика Шуберта о числе возможных задач при "игре в 15".
'Игра в 15'
"Сколько всего возможно задач; т. е. сколько различных расположений можно дать 15 шашкам, при чем каждый раз пустое поле расположено справа внизу? Чтобы определить, сколько перестановок можно получить с помощью 15 предметов, начнем с 2-х предметов: а и b. Они могут дать лишь две перестановки, именно - аb и bа. При трех предметах имеется уже втрое больше перестановок, т. е. 6, так как предмет "а" может быть поставлен перед bc и перед cb, и кроме того, имеются еще две перестановки, начинающиеся с b, и две начинающиеся с с. Отсюда можно заключить, что четыре предмета а, b, с, d могут дать вчетверо большее число различных перестановок, т. е. 4 × 3 × 2 = 24 перестановки. Продолжая так, можно найти, что 15 шашек допускают всего
2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 × 11 × 12 × 13 × 14 × 15
перестановок. Вычислив это произведение, мы найдем для числа задач игры внушительное число:
1 биллион 307674 миллиона 365000".
Из этого огромного числа задач ровно половина принадлежит к разрешимым и столько же - к неразрешимым. Заметим еще, что если бы возможно было ежесекундно давать шашкам новое положение, то чтобы перепробовать всевозможные расположения, потребовалось бы, при непрерывной работе круглые сутки, - свыше 40000 лет.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'