ДИСКРИМИНАНТНАЯ КРИВАЯ

ДИСКРИМИНАНТНАЯ КРИВАЯ обыкновенного дифференциального уравнения 1-го порядка F(x, у, y') = 0 - множество точек (х, у) плоскости, координаты которых удовлетворяют уравнению φ(х, у) = 0, получающемуся исключением у' из соотношений F = 0 и F'_y' = 0 или исключением х из соотношений G = 0 и G'_x' = 0, где G (у, х, x') ≡ F(x, у, 1/х') (в предположении, что F'_y' существует). Если Д. к. для уравнения F = 0 - непустое множество и не вырождается в отдельные точки, то она (или каждая ее ветвь) может:

1) являться решением уравнения F=0, в каждой точке которого нарушается единственность, - в таком случае Д. к. есть огибающая семейства интегральных кривых (напр., у = 1 и y = -1 для уравнения у'² + у² - 1 = 0, рис. 1; y = 0 для уравнения y'³ - y² = 0, рис. 2); 2) являться решением уравнения F = 0, в каждой точке к-рого имеет место единственность (напр., у = 0 для уравнения y'² - y² = 0, рис. 3); 3) не являться решением уравнения F = 0, в таком случае Д. к. есть множество либо точек возврата интегральных кривых

(например, х = 0 для уравнения у'² - х = 0, рис. 4), либо точек прикосновения различных интегральных кривых (например. х = 0 для уравнения у'² - х² = 0, рис. 5).

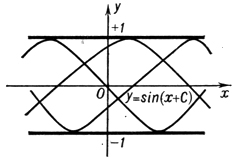
Рис. 1.

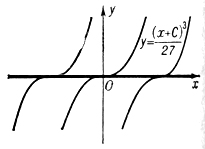
Рис. 2.

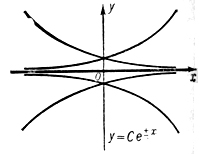
Рис. 3.

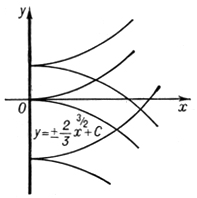
Рис. 4.

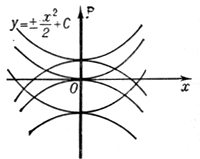
Рис. 5.

Рассматривается также уравнение F = 0 в комплексной области. когда F - многочлен от у' (см., напр.. [2], гл. II).

Лит.: [1] Сансонс Дж., Обыкновенные дифференциальные уравнении, пер. с итал., т. 2, М., 1954; [2] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М.-Л., 1950.

Н. X. Розов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.