ДИОФАНТОВЫХ УРАВНЕНИЙ ПРОБЛЕМА РАЗРЕШИМОСТИ

ДИОФАНТОВЫХ УРАВНЕНИЙ ПРОБЛЕМА РАЗРЕШИМОСТИ — проблема отыскания алгоритма для распознавания по любому диофантову уравнению, имеет ли оно решение.

Существенным в постановке проблемы является требование найти универсальный метод, к-рый должен быть пригоден для любого уравнения (все известные способы для распознавания наличия решений у диофантовых уравнений применимы лишь к уравнениям из отдельных более или менее широких классов). Такой метод позволял бы решать и системы диофантовых уравнений, ибо система Р₁ = 0, ..., Р_k = 0 эквивалентна уравнению

Р²₁ + , ..., + Р²_k = 0.

Задача нахождения такого универсального метода для распознавания наличия решений в целых числах была поставлена Д. Гильбертом (D. Hilbert, см. [1]).

В начале 50-х гг. 20 в. появились первые работы, нацеленные на доказательство невозможности алгоритма, требуемого в Д. у. п. р. В это время была высказана гипотеза (гипотеза Дейвиса, см. [2]) о том, что каждое перечислимое множество является диофантовым множеством. Поскольку известны примеры перечислимых, но алгоритмически неразрешимых множеств, то из справедливости этой гипотезы немедленно следует отрицательное решение Д. у. п. р.

В 1961 было доказано (см. [3]) более слабое утверждение: каждое перечислимое множество является показательно-диофантовым множеством, т. е. для каждого перечислимого множества 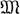существуют такие выражения А и L, построенные из натуральных чисел и переменных a, z₁, ..., z_n с помощью сложения, умножения и возведения в степень, что а ∈ 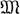тогда и только тогда, когда показательно-диофантово уравнение K = L разрешимо относительно z₁, ..., z_n. После этого для доказательства гипотезы Дейвиса осталось указать способ, позволяющий преобразовать произвольное показательно-диофантово уравнение в нек-рое диофантово уравнение, имеющее или не имеющее решения одновременно с ним. Было доказано [4], что такое преобразование возможно, если существует диофантово уравнение

G(u, v, z₁, ..., z_k) = 0, обладающее следующими двумя свойствами: 1) в любом решении этого уравнения v ≤ uⁿ 2) для любого к существует решение, в к-ром v > uk (про такое уравнение говорят, что оно имеет экспоненциальный рост). Пример диофантова уравнения, имеющего экспоненциальный рост, к-рый впервые был построен в [5], завершил доказательство гипотезы о диофантовости перечислимых множеств (полностью доказательство гипотезы Дейвиса изложено в [6], [7]). Обратное утверждение о перечислимости диофантовых множеств доказывается легко. Таким образом, класс перечислимых множеств совпадает с классом диофантовых множеств.

Из этого результата следует возможность указать конкретный многочлен W(a, z₁, ..., z_n) с целыми коэффициентами такой, что не существует алгоритма, позволяющего по значению параметра а узнавать, разрешимо ли уравнение W(a, z₁, ..., z_n) = 0 относительно z₁, ..., z_n, и, тем более, не существует требуемого в Д. у. п. р. алгоритма для распознавания наличия решений у произвольного диофантова уравнения.

Вопрос о существовании алгоритма, позволяющего распознавать разрешимость диофантовых уравнений в рациональных числах, эквивалентен вопросу о существовании алгоритма, позволяющего распознавать разрешимость однородных диофантовых уравнений в целых числах. Эта важная проблема пока (1978) остается открытой и малоисследованной.

Лит.: [1] Гильберт Д., в кн.: Проблемы Гильберта, М., 1969, с. 11-64; [2] Дэвис М., «Математика», 1964, т. 8, № 5, с. 15-22; [3] Дэвис М., Путнам Х., Робинсон Дж., там же, с. 69-79; [4] Робинсон Дж., там же, с. 3-14; [5] Матиясевич Ю. В., «Докл. АН СССР», 1970, т. 191, №2, с. 279-82; [6] его же, «Успехи матем. наук», 1972, т. 27, в. 5, с. 185-222; [7] Манин Ю. И., в сб.: Итоги науки и техники. Современные проблемы математики, 1973, т. 1, с. 5-37; [8] Davis М., Матиясевич Ю. В., Robinson J., «Рrос. Symp. Pure Math.», 1976, v. 28, p. 323-75.

Ю. В. Матиясевич.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.