ДИНИ-ЛИПШИЦА ПРИЗНАК

ДИНИ-ЛИПШИЦА ПРИЗНАК: если непрерывная 2π-периодич. функция f(x) удовлетворяет условию

lim_δ→+0 ω(δ, f) ln 1/δ = 0,

где ω(δ, f) - модуль непрерывности функции f(x), то ее ряд Фурье равномерно сходится к ней на всей числовой оси. Д.-Л. п. доказан У. Дини а в частном случае, когда ω(δ, f) = O(δ^α), δ → +0, при каком-либо 0 < α ≤ 1, он установлен Р. Липшицем [2]. Утверждение Д.-Л. п. окончательно в следующем смысле. Если ω(δ) - произвольный модуль непрерывности, удовлетворяющий условию

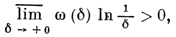
то существует непрерывная 2π-периодич. функция f₀(x), ряд Фурье которой расходится в некоторой точке, а модуль непрерывности ω(δ, f₀) удовлетворяет условию ω(δ, f₀) = O(ω(δ)).

Лит.: [1] Dini U., Sopra la serie di Fourier, Pisa, 1872; [2] Lipschitz R., «J. reine und angew. Math»., 1864, Bd 63, № 2, S. 296-308; [3] Lebesgue H., «Bull. Soc. math. France» 1910, t. 38, p. 184-210; [4] Hикольский С. М., «Докл. АН СССР», 1950, т. 73, № 3, с. 457-60; [5] Бари Н. К., Тригонометрические ряды, М., 1961.

Б. И. Голубов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.