ГАРМОНИЧЕСКИЙ МНОГОЧЛЕН

ГАРМОНИЧЕСКИЙ МНОГОЧЛЕН - 1) Г. м. - многочлен по переменным x₁, ..., x_n, удовлетворяющий Лапласа уравнению. Любой Г. м. может быть представлен в виде суммы однородных Г. м. При n = 2 среди однородных Г. м. степени m имеется только два линейно независимых, напр. действительная и мнимая части в выражении (x₁ + ix₂)^m. При n = 3 число линейно независимых однородных Г. м. степени m равно 2m + 1. В общем случае n ≥ 2 число линейно независимых однородных Г. м. степени m равно

K^m_n - K^m-2_n, m ≥ 2,

где

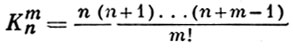
- число размещений из n по m с m повторениями. Однородные Г. м. V_m(х) наз. также шаровыми функциями (в особенности при n = 3). При n = 3 введение сферич. координат позволяет записать:

V_m(x) = r^mY_m(θ, φ),

где

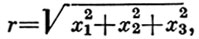
a Y_m(θ, φ) есть сферическая функция степени m.

Лит.: [1] Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; [2] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М.. 1966; [3] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964.

Е. Д. Соломенцев.

2) Г. м. - конечная линейная комбинации гармоник. Действительнозначные Г. м. представимы в виде

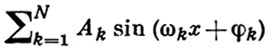
при нек-ром натуральном N, неотрицательных A_k, действительных ω_k, φ_k, k = 1, 2, ..., N. Комплекснозначные Г. м. представимы в виде

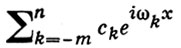
при натуральных значениях m, n, действительных значениях ω_k и комплексных значениях с_k, k = -m, -m+1, ..., n. Г. м. являются простейшими почти периодическими функциями

В. Ф. Емельянов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.