ВЫПУКЛАЯ ФУНКЦИЯ

ВЫПУКЛАЯ ФУНКЦИЯ комплексного переменного z - регулярная однолистная функция

w = f(z) = c₀ + c₁z + c₂z² + ...

в единичном круге E = {z; |z| < 1}, отображающая единичный круг на нек-рую выпуклую область. Регулярная однолистная функция w = f(z) является В. ф. тогда и только тогда, когда при обходе любой окружности |z| = r, 0 < r < 1, касательная к образу |z| = r в точке f(z) вращается в одном и том же направлении. Следующее неравенство выражает необходимое и достаточное условие выпуклости f(z):

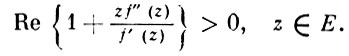
(1)

С другой стороны, для того чтобы f(z) была В. ф., необходимо и достаточно, чтобы она допускала следующее параметрич. представление:

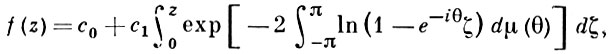
(2)

где μ(θ) - неубывающая действительная функция на отрезке [-π, π] такая, что

с₀, с₁ - комплексные постоянные, с₁ ≠ 0. Формулу (2) можно рассматривать как обобщение Кристоффеля-Шварца формулы для отображения круга Е на выпуклые многоугольники.

Пусть S⁰ - класс всех В. ф. в Е, нормированных условиями с₀ = f(0) = 0, c₁ = f'(0) = 1; S⁰_p, p = 1, 2, ..., суть подклассы класса S⁰, состоящие из функций, отображающих Е соответственно на выпуклые области плоскости w с р-кратной симметрией вращения относительно точки w = 0, S₁⁰ = S⁰. Классы S_p⁰p компактны в себе относительно равномерной сходимости внутри Е. Их интегральные представления, в частности формула (2) для S⁰, позволяют развить вариационные методы решения экстремальных задач на классах S⁰_p (см. [2] - [5]).

Основные экстремальные свойства класса S⁰ характеризуются следующими неулучшаемыми неравенствами:

|с_n| ≤ 1, n = 2, 3, ..., |z|(1 + |z|)^-1 ≤ |f(z)| ≤ |z|(1 - |z|)^-1, (1 + |z|)^-2 ≤ |f'(z)| ≤ (1 - |z|)^-2, |arg f'(z)| ≤ 2 arc sin |z|, z ∈ E,

под аргументом функции понимается ветвь, обращающаяся в нуль при z = 0. Во всех этих оценках знак равенства имеет место только для функции f(z) = z/(1 - εz), |ε| = 1. Для отношения К_r кривизны K(r) границы ∂B_r(f) области B_r(f) = {w = f(z); |z| < r} на классе S⁰_p, p = 1, 2, ..., в точке f(z) к кривизне 1/r прообраза ∂B_r(f), т. е. окружности |z| = r, в точке z имеются также неулучшаемые оценки. Областям B₁(f), f ∈ S⁰, принадлежит круг |w| < 1/2, причем радиус этого круга не может быть увеличен без дополнительных ограничений на класс функций. Если f(z) ∈ S⁰, то однолистная функция g(z) = zf'(z) звездообразна в круге Е, т. е. отображает Е на область, звездную относительно начала координат.

Примерами обобщения и видоизменения класса S⁰ и его подклассов являются: класс Σ⁰ однолистных в |z| > 1 функций F(z) = z + d₀ + d₁z^-1 + ...,регулярных при 1 < |z| < ∞ и отображающих |z| > 1 на области с выпуклыми дополнениями; класс S⁰(r, R) регулярных в кольце r < |z| < R нормированных определенным образом функций F(z), каждая из к-рых однолистно отображает это кольцо в такую область, что конечная компонента ее дополнения выпукла и ее объединение с этой компонентой также выпукло; класс S⁰_pr функций из S⁰_p с действительными коэффициентами разложений Тейлора в окрестности точки z = 0. Понятие В. ф. распространяется и на многолистные функции (см. [2], добавление).

Самостоятельный интерес представляет следующее обобщение В. ф. (см. [6]): регулярная в круге Е функция w = f(z) = z + c₂z² + ... наз. близкой к выпуклой, если существует в Е В. ф. Ф(z), Ф(0) = 0, такая, что всюду в Е

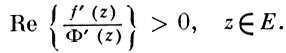
Для класса K всех таких функций f(z) доказана однолистность, найдены необходимые и достаточные условия принадлежности функции f(z) классу K и параметрич. представление функций f(z) ∈ K при помощи интегралов Стилтьеса:

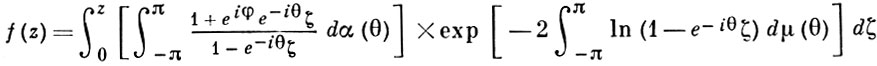
где |φ| < π; α(θ), μ(θ) - неубывающие действительные функции,

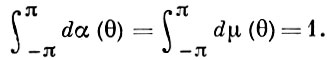
Класс K включает в себя выпуклые, звездные и другие функции. Для функций f(z) ∈ К справедлива Бибербаха гипотеза: |с_n| ≤ n; известны неулучшаемые оценки:

|z|(1 + |z|)^-2 ≤ |f(z)| ≤ |z| (1 - |z|)^-2, (1 -|z|)(1 + |z|)^-3 ≤ |f'(z)| ≤ (1 + |z|)(1 - |z|)^-3, |arg f'(z)| ≤ 4 arc sin |z|, z ∈ E,

под аргументом функции понимается ветвь, обращающаяся в нуль при z = 0. Во всех этих оценках знак равенства имеет место только для функции f(z) = z/(1 - εz)², |ε| = 1. Геометрически функции f(z) класса K характеризуются тем, что они отображают круг Е на области D(f), внешность к-рых CD̄(f) может быть заполнена лучами L, проведенными из точек границы области, L ⊂ CD(f). Понятие функции, близкой к выпуклой, распространено на многолистные функции (см. [7]).

Лит.: [1] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [2] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [3] Зморович В. А., «Укр. матем. ж.», 1952, т. 4, с. 276-98; [4] Александров И. А., Черников В. В., «Сиб. матем. ж.», 1963, т. 4, № 2, с. 261-67; [5] Зморович В. А., «Матем. сб.», 1953, т. 32, № 3, с. 633-52; [6] Карlan W., «Michigan Math. J.», 1952, v. 1, № 2, p. 169-85; [7] Styer D., «Trans. Amer. Math. Soc.», 1972, v. 169, p. 105-12.

И. А. Александров, Ю. Д. Максимов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.