ВИТТА ВЕКТОР

ВИТТА ВЕКТОР - элемент алгебраич. конструкции, впервые предложенной Э. Виттом в 1936 [1] в связи с описанием неразветвленных расширений полей р-адических чисел. Позже В. в. были применены при изучении алгебраических многообразий над полем положительной характеристики (см. [3]), а также в теории коммутативных алгебраических групп (см. [4], [5]) и в теории формальных групп (см. [6]). Пусть A - ассоциативно-коммутативное кольцо с единицей. Векторами Виттас компонентами в А наз. бесконечные последовательности а = (а₀, а₁, ...), а_i ∈ A, к-рые складываются и перемножаются по следующим правилам:

(а₀, a₁, ...) + (b₀, b₁, ...) = (S₀(a₀, b₀), S₁(а₀, а₁; b₀, b₁, ...),

(а₀, a₁, ...) × (b₀, b₁, ...) = (M₀(a₀, b₀), M₁(a₀, а₁; b₀, b₁), ...),

где S_n, M_n - многочлены от переменных X₀, ..., X_n, Y₀, ..., Y_n с целыми коэффициентами, однозначно определяемые условиями

Ф_n(S₀, ..., S_n) = Ф_n(Х₀, ..., X_n) + Ф_n(Y₀, ..., Y_n),

Ф_n(М₀, ..., M_n) = Ф_n(X₀, ..., X_n) ⋅ Ф_n(Y₀, ..., Y_n);

здесь

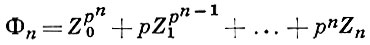
- многочлены, n ∈ N, р - простое число. В частности,

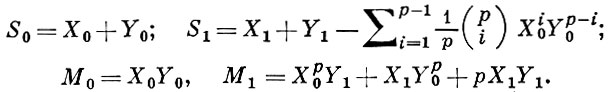
В. в. с введенными выше операциями образуют кольцо, наз. кольцом векторов Витта и обозначаемое W(A). Для любого натурального n определено также кольцо W_n(A) усеченных векторов Витта длины n. Элементы этого кольца являются конечными наборами а = (а₀, ..., a_n-1), a_i ∈ A, с операциями сложения и умножения, приведенными выше. Канония. отображения:

R: W_n+1(А) → W_n(А), R((а₀, ..., а_n)) = (а₀, ..., а_n-1), T: W_n(A) → W_n+1(A), Т((а₀, ..., a_n-1)) = (0, а₀, ..., a_n-1)

являются гомоморфизмами. Сопоставление A → W(A) (соответственно A → W_n(A)) определяет ковариантный функтор из категории коммутативных колец с единицей в категорию колец. Этот функтор представим кольцом многочленов Z[X₀, ..., Х_n, ...] (соответственно Z[X₀, ..., X_n-1]), на к-ром определена структура кольцевого объекта. Спектр Spec Z[Х₀, ..., Х_n, ...] (соответственно Spec Z[Х₀, ..., X_n-1) наз. схемой Витта (соответственно усеченной схемой Витта) и является кольцевой схемой [3].

Каждый элемент а ∈ А определяет В. в.

а^τ = (а, 0, 0, ...)r ∈ W(A),

наз. представлением Тейхмюллера элемента а. Если А = k - совершенное поле характеристики р > 0, то W(k) является полным кольцом дискретного нормирования характеристики нуль с полем вычетов к и максимальным идеалом pW(k). При этом каждый элемент w ∈ W(k) однозначно записывается в виде

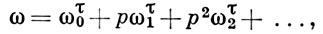
где ω_i ∈ k. Наоборот, каждое такое кольцо А с полем вычетов k = А/р канонически изоморфно кольцу W(k). Представление Тейхмюллера позволяет построить канонический мультипликативный гомоморфизм k → W(k), расщепляющий отображение

W(k) → W(k)/р ≃ k.

Если k = F_p - простое поле из р элементов, то W(F_p) есть кольцо целых р-адических чисел Z_p.

Лит.: [1] Witt Е., «J. reine und angew. Math.», 1936, Bd 176, S 176-240; [2] Ленг С., Алгебра, пер. с англ., М., 1968; [3] Мамфорд Д., Лекции о кривых на алгебраической поверхности, пер. с англ., М., 1968; [4] Серр Ж. П., Алгебраические группы и поля классов, пер. с франц., М., 1968; [5] Demazure М., Gabriel P., Groupes algebriques, t. 1, P.-Amst., 1970; [6] Dieudonné J., «Math. Ann.», 1957, Bd 134, S. 114-33.

И. В. Долгачев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.