БОРЕЛЯ ПРЕОБРАЗОВАНИЕ

Расстановка ударений: БОРЕ`ЛЯ ПРЕОБРАЗОВА`НИЕ

БОРЕЛЯ ПРЕОБРАЗОВАНИЕ - интегральное преобразование вида

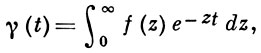
где f(z) - целая функция экспоненциального типа. Б. п. есть частный случай Лапласа преобразования. Функция γ (t) наз. ассоциированной функцией (по Борелю) с f(z). Если

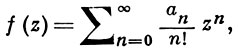
то

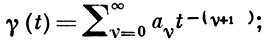
ряд сходится при |t| > σ, где σ - тип функции f(z). Пусть D¯ - наименьшее выпуклое замкнутое множество, содержащее все особенности функции γ (t),

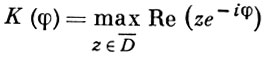
- опорная функция множества D¯ и h(φ) - индикатриса роста функции f(z). Тогда K(φ) = h(- φ). Если интегрирование в Б. п. происходит по лучу arg z = φ, то соответствующий интеграл сходится в полуплоскости х cos φ + у sin φ > K(- φ). Пусть С - замкнутый контур, охватывающий D¯. Тогда

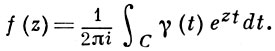
При дополнительных условиях из этой формулы могут быть выведены и другие представления. Так, пусть имеется класс целых функций f(z) экспоненциального типа ≤ σ, для к-рых

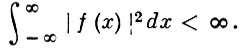
Этот класс совпадает с классом функций f(z), допускающих представление

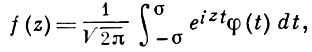
где φ (t) ∈ L² (- σ, σ).

Лит. : [1] Вorel Е., Lecons sur les séries divergentes, 2 ed., P., 1928; [2] Джрбашян М. M., Интегральные преобразования и представления функций в комплексной области, М., 1966.

А. Ф. Леонтьев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.