АБСОЛЮТНЫЙ МОМЕНТ

Расстановка ударений: АБСОЛЮ`ТНЫЙ МОМЕ`НТ

АБСОЛЮТНЫЙ МОМЕНТ случайной величины X - математич. ожидание |Х|^r, r > 0. Обычное обозначение А. м. β_r ; таким образом,

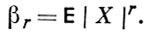
Число r наз. порядком А. м. Если F(х) - функция распределения X, то

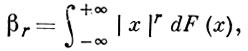
(1)

и, напр., если распределение X имеет плотность р (х), то

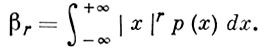
(2)

В соответствии с (1) и (2) говорят об А. м. функции распределения F(х) или плотности р(х). Из существования β_r вытекает существование А. м. β_r', а также моментов порядка r', 0 < r' < r. А. м. часто фигурируют в оценках для распределений вероятностей и их характеристич. функций (см. Чебышева неравенство, Ляпунова теорема). Функция logβ_r является выпуклой функцией от r, а функция β^1/r_r - неубывающей функцией от r(r > 0).

Ю. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.