4.5. Многотуровые экспертизы и их моделирование

Здесь мы расскажем о двух способах "борьбы" с необъективностью экспертов. Один из них состоит в организации многотуровой экспертизы: экспертам предлагается несколько раз высказать свое мнение по одному и тому же вопросу. При этом каждому эксперту может быть сообщена (или не сообщена) некоторая информация о предыдущих турах; например, мнения других экспертов или общая усредненная оценка. Естественно, что получение дополнительной информации позволяет экспертам в ходе повторных туров корректировать свои заключения.

Другой способ состоит в моделировании (а не фактической реализации) многотуровой экспертизы. При этом используются только одноразовые высказывания экспертов, а целью является корректировка их среднего мнения [15, 16].

Остановимся более подробно на этом методе. Обозначим, как и раньше, буквой R множество возможных отношений с определенной на нем метрикой d(r_i, r_j) (см. с. 49). Допустим, что экспертная комиссия состоит из n экспертов. Обозначим через r⁰_i "объективное" отношение i-го эксперта, а через r^*_i - его "субъективное" (конъюнктурное) отношение. Реальное существование двух таких различных мнений почти бесспорно. В самом деле, например, всякий спортивный судья, с одной стороны, создает для себя "объективную" оценку выступления спортсмена, а с другой, как представитель своей страны или группы стран, являясь приверженцехм некоторой школы (направления), представителем некоторого спортивного общества, он не может отвлечься от своей "субъективной" (несколько пристрастной) точки зрения.

Естественно предположить, что i-й эксперт всегда высказывает отношение, заключенное между r_i⁰ и r^*_i.

Рассмотрим следующий интересный и важный пример. Судья выставляет фигуристу две оценки: одну за техническое мастерство, а другую - за художественное впечатление. Место, присужденное спортсмену данным судьей, определяется суммой этих двух оценок. Допустим, что отношение r⁰ = (5,7; 5,8) выражает "объективное", а отношение r^* = (5,4; 5,3) - "субъективное" мнение судьи. Множеством отношений, лежащих между r⁰ и r^*, будут такие пары оценок, сумма элементов которых будет больше 10,7, но меньше 11,5. Это множество точек изображено на рис. 10 и определяется следующими ограничениями-неравенствами:

где x - оценка за техническое мастерство, а y - за художественное впечатление.

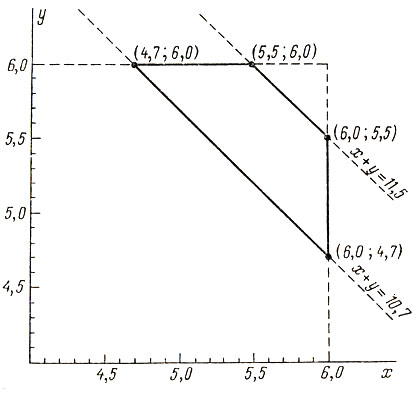
Рис. 10

Геометрия множества отношений, лежащего между двумя заданными отношениями, может быть весьма разнообразной. В частности, если каждым судьей выставляется лишь одна оценка, как например в спортивной гимнастике, то мы можем иметь дело с обычным отрезком числовой оси.

Предположим, что эксперты выдали n отношений r₁, r₂, ..., r_n. Решив задачу отыскания медианы Кемени (см. с. 50), мы находим среднее отношение 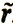₁ выданных экспертами отношений. После этого найдем расстояния d(r_i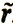1) от этого среднего до отношения r_i для всех i = 1, ..., n. Наконец, введем условные коэффициенты объективности ось α₁, α₂, ..., α_n судей по формулам

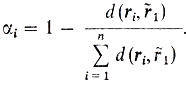
Таким образом, чем ближе r_i к среднему отношению 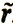₁ тем больше коэффициент объективности. Учитывая коэффициенты объективности, найдем новое среднее отношение 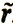₂, которое минимизирует сумму расстояний до отношений α₁r₁, α₂r₂, ..., α_nr_n, вновь повторяем эту операцию и т. д. В пределе получим отношение r, которое и следует выбрать в качестве среднего.

На практике часто оказывается достаточным найти отношение 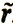₂, так как даже оно уже оказывается близким к истинной медиане Кемени "объективных" мнений r⁰₁, ..., r⁰_n.

В свете изложенных выше соображений становится интересным обсудить судейство в гимнастике и в соревнованиях по прыжкам в воду. В этих видах спорта при выведении балла отбрасываются наименьшая и наибольшая оценки, что, естественно, положительно отражается на объективности судейства. Кроме того, в гимнастике главный судья или жюри могут изменить оценку выступления спортсмена на каком-либо снаряде в случае, когда мнения судей резко расходятся. Рассмотрим теперь математические модели судейства в спортивной гимнастике более подробно.