Глава 1. Числа, равенства и неравенства

1. Упражнение по таблице умножения

Строим следующую последовательность цифр.

Пусть первой цифрой будет 2, следующей 3,

третьей цифрой последовательности будет 6;

четвертой цифрой будет 1, а пятой 8;

шестой цифрой является 6, затем следует цифра 8 и т. д. Вот последовательность цифр, которую мы получим:

Дужки внизу между цифрами означают выполненные умножения, результаты которых мы уже вписали как очередные цифры последовательности; например, теперь следовало бы умножить 8 на 6 и вписать цифры результата: 4, 8. Недостатка в множимых цифрах у нас никогда не будет, так как при каждом умножении дужки передвигаются на один шаг, а полученный результат по меньшей мере однозначен, а часто и двузначен, и поэтому прибавляется по меньшей мере одна цифра.

Доказать, что цифры 5, 7, 9 никогда не появятся в этой последовательности.

2. Интересное свойство чисел

Напишем произвольное натуральное число в десятичной системе счисления (например, 2583) и вычислим сумму квадратов цифр этого числа (2² + 5² + 8² + 3² = 102). С полученным числом проделаем то же самое (1² + 0² + 2² = 5) и будем поступать таким же образом и далее

Доказать, что если этот процесс не приведет нас к единице (ясно, что после этого единица будет повторяться бесконечное число раз), то наверняка приведет к числу 145, после чего появится цикл

который далее будет все время повторяться.

3. Делимость на 11

Доказать, что при любом натуральном k число 5^5k+1 + 4^5k+2 + 3^5k делится на 11.

4. Делимость чисел

Число 3¹⁰⁵ + 4¹⁰⁵ делится на 13, 49, 181 и 379, но не делится на 5 и 11. Как это проверить?

5. Облегченная теорема Ферма

Если х, y, z, n - натуральные числа, причем n > z, то равенство xⁿ + yⁿ = zⁿ невозможно.

6. Расстановка чисел

Найти 10 таких чисел х₁, х₂, х₃, х₄, . . ., x₁₀, чтобы

число x₁ находилось внутри отрезка [0, 1],

числа x₁ и х₂ по одному находились в первой и второй половинах этого отрезка,

числа x₁, х₂, х₃ по одному находились в каждой из трех равных частей отрезка,

числа х₁, х₂, х₃, х₄ по одному находились в каждой четверти этого отрезка и т. д., наконец, чтобы

числа х₁, х₂, . . ., x₁₀ по одному находились в каждой из частей отрезка [0, 1], полученных путем его деления на 10 равных отрезков.

7. Обобщение

Разрешима ли предыдущая задача, если вместо 10 искать n чисел (n - произвольное натуральное число), удовлетворяющих п аналогичным условиям?

7а. Перестановка букв

Из комплекса букв aabbcc можно получить 90 различных перестановок. Из перестановки aabcbc можно получить перестановку aacbcb, записывая букву с вместо буквы b и букву b вместо буквы с; из перестановки aacbcb можно получить перестановку bcbcaa, если прочесть ее в обратном порядке, а из этой последней перестановки путем замены букв можно получить перестановку acacbb, и т. д.

Все такие перестановки, как aabcbc, aacbcb, bcbcaa, acacbb, мы считаем несущественно различными. Перестановки же, как, например, aabcbc и abcbca, мы считаем существенно различными, так как ни замена букв, ни прочитывание их в обратном порядке, ни многократное применение этих операций не могут преобразовать один комплекс в другой.

Вопрос: сколько имеется существенно различных перестановок букв aabbcc?

8. Пропорция

Числа А, В, С, р, q, r связаны между собой соотношениями

Записать пропорции

A : B : С = □ : □ : □

в таком виде, чтобы на пустых местах появились выражения, состоящие из р, q, r, и чтобы эти выражения получались одно из другого путем циклической перестановки букв р, q, r. (Мы понимаем это следующим образом: если вместо р напишем q, вместо q напишем r, а вместо r напишем р, то первое выражение преобразуется во второе, второе - в третье, а третье - в первое).

8а. Симметрические выражения

Такие выражения, как x+y+z или xyz, являются симметрическими. Под этим мы понимаем, что их значение не меняется при перестановке в них переменных x, y, z каким угодно образом. Приведенные выше примеры очевидны; но существуют симметрические выражения, симметричность которых не является очевидной, например: ||x-y|+x+y-2z|+|x-y|+x+y+2z.

Докажите симметричность этого выражения и определите его значение таким образом, чтобы симметричность стала, очевидной.

9. Иррациональность корня

Докажите элементарным путем, что положительный корень уравнения

является иррациональным.

10. Неравенство

Доказать неравенство

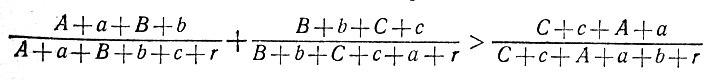
в котором все буквы обозначают положительные числа.

11. Числовые последовательности

Найти последовательность а₀, а₁, а₂, ... положительных чисел такую, что а₀ = 1 и а_n-а_n+1=а_n+2 при n = 0, 1, 2, ... Показать, что существует только одна такая последовательность.