
§ 3. Вычислительный метод динамического программирования для задачи распределения с одним ограничением [8]
Прежде всего условимся считать все xj, aj и b в задаче (3.1) целыми Требование целочисленности aj и b фактически не является принципиальном, так как оно Может быть в большинстве случаев выполнено с необходимой степенью точности. Действительно, сделанное допущение задает лишь выбор единиц измерения величин aj и b. Например, если b есть денежные единицы, то переход от тысяч к сотням или от сотен к десяткам и единицам рублей и т. д. всегда позволяет выразить b целым числом. То же самое относится и к aj. Причина введения требования целочисленности xj, aj и b станет ясна ниже.
Выше уже говорилось, что планирование многошагового процесса должно производиться на каждом шаге с учетом будущего. Однако среди всех шагов последний шаг является шагом, для которого будущее не играет роли, так как на этом шаге по условию задачи процесс заканчивается, т. е. последний шаг можно планировать таким образом, чтобы он сам по себе приносил максимальную выгоду. Спланировав оптимальным образом этот последний шаг, можно к нему пристраивать предпоследний таким образом, чтобы результат этих двух шагов был оптимальным, и т. д. Процесс решения в динамическом программировании разворачивается в обратном направлении, т. е. от конца к началу. Продемонстрируем подробнее схему такой процедуры.
Прежде всего планируется последний шаг. Мы можем это сделать, не заглядывая в будущее, однако нам необходимо знать, чем кончился предпоследний шаг. Поскольку мы этого не знаем, то, очевидно, необходимо сделать разные предположения о том, чем кончился предпоследний шаг, и для каждого из этих предположений выбрать переменные (управления) таким образом, чтобы на последнем шаге получить оптимальное решение. Такое оптимальное управление, задаваемое в условиях предположения о том, чем кончился предыдущий шаг, называется условным оптимальным управлением.
Итак, обозначим через Z* абсолютный максимум Z в (3.1), т. е. величину, которую мы хотим найти:
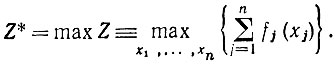
(3.2)
Выберем некоторое значение xn и, зафиксировав его, предположим, что мы можем определить максимум Z относительно всех остальных переменных x1, x2, ..., xn-1. Конечно, при этом величины x1, x2, ..., xn-1 при которых достигается maxx1, ..., xn-1 Z, будут зависеть от выбранного нами значения xn.
Поскольку мы условились, что xn - целые числа, то можно представить, что эта максимизация выполнена для всех возможных значений xn. Тогда Z* будет наибольшим из всех полученных при этом значений Z. Таким образом, можно написать:
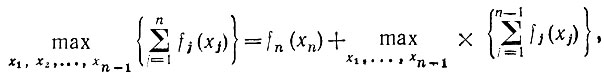
(3.3)
где член fn (xn) вынесен из-под знака максимума, поскольку величина xn - фиксированная. Значения x1, x2, ..., xn-1; кроме условий целочисленности и неотрицательности, очевидно, должны удовлетворять ограничению, которое при фиксированном xn записывается в виде
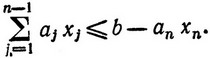
(3.4)
Так как согласно (3.4) значения x1, x2, ..., xn-1 зависят от величины ξ = b - anxn, то величина
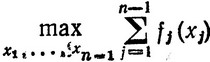
является функцией ξ, т. е. можно обозначить
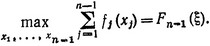
(3.5)
Допустим, что нам удалось вычислить Fn-1 (ξ) для всех допустимых значений xn. Тогда можем написать:
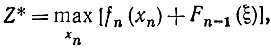
(3.6)
где xn может принимать значения 0, 1, 2, ... 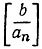 и
и 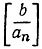 обозначает целую часть от величины b/an. Мы можем найти Z*, если вычислим
обозначает целую часть от величины b/an. Мы можем найти Z*, если вычислим
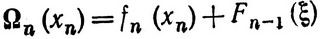
для всех допустимых значений xn и затем возьмем наибольшую величину Ωn (xn*), где через xn* обозначено значение xn, при котором достигается этот максимум. Таким образом, если бы была известна функция Fn-1 (ξ), то задача отыскания Z* свелась бы к задаче максимизации функции одной переменной. Условно считая, что переменная xn уже выбрана, т. е. последний шаг спланирован для любого Fn-1 (ξ), и поступая аналогично вышеизложенному по отношению к переменной xn-1, запишем соотношение
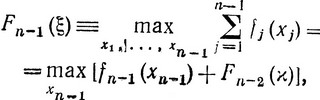
(3.7)
где א = ξ - an-1xn-1,
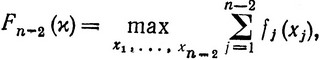
(3.8)
и максимум в (3.8) берется по неотрицательным целым числам x1, ..., xn-2, удовлетворяющим условию
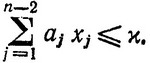
(3.9)
Величина xn-1 в (3.7) может принимать значения 0, 1, 2, ..., [ξ/an-1]. Поэтому, если бы была известна функция Fn-2 (א), можно было бы вычислить Fn-1 (ξ), взяв максимум только по одной переменной xn-1. Однако в отличие от (3.6) максимум в (3.8) должен вычисляться также для всех возможных значений ξ.
Используя последовательно этот прием для вычисления Fn-2, Fn-3 и т. д., мы, наконец, придем к вычислению

(3.10)
где x1 в свою очередь может принимать значения 0, 1, ..., [ρ/a1].
Итак, лишь F1 определяется непосредственно, остальные Fk (k = 2, 3, ..., n) определяются с помощью соотношений вида
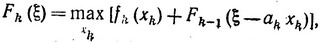
(3.11)
где xk может принимать значения 0, 1, 2, ..., [ξ/ak] (под ξ подразумевается любая из величин ξ, א, ..., ρ) и Z* = Fn (b). Величина ξ называется параметром состояния; функции Fk (ξ) - функциями состояния.
Соотношения вида (3.11), обладающие тем свойством, что значение функции, вычисленное с помощью данного соотношения, подставляется как аргумент в следующее соотношение, называются реккурентными соотношениями.
Таким образом, в результате последовательного прослеживания всех шагов от конца к началу многошагового процесса мы получили выражения, с помощью которых можно найти максимальные значения Z на всех шагах, используя соответствующие условные оптимальные управления, т. е. схему вычислительного метода динамического программирования. Покажем теперь, каким образом довести вычисления до конца, т. е. найти множество значений x1*, x2*, ..., xn*, определяющих оптимальное управление.
Прежде всего необходимо определить
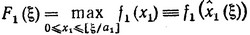
(3.12)
Для всех g=ξ = 0, 1, 2, ..., b. Здесь через x1^ (ξ) обозначена величина x1, при которой достигается максимум. Это значение F1 может быть не единственным, т. е. соотношение (3.12) может выполняться более чем для одного значения x1^ (ξ). Если необходимо найти все оптимальные решения, то для каждого ξ следует определить все x1, для которых выполняется соотношение (3.12). Например, если a1 = 1, то при ξ = 0 величина x1 может принимать только одно значение x1 = 0 и соответственно F1 (0) = f1(0). При ξ = 1 имеем x1 = 0 и x1 = 1, вычисляем f (1), сравниваем f1 (0) и f1 (1) и выбираем большее: F1 (1) = max [f1 (0), f1 (1)] и т. д. до ξ = b. При ручном счете значения оказывается удобно записывать в виде таблиц; при счете на ЭВМ эти значения хранятся в памяти машины.
Найдя F1 (ξ), с помощью (3.11) определяем
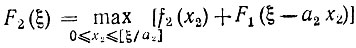
(3.13)
опять для всех ξ = 0, 1, ..., b. При этом для вычисления F2 (ξ) при фиксированном ξ последовательно в (3.13) придаем x2 целочисленные значения из интервала 0≤x2≤[ξ/a2] и получаем последовательность величин
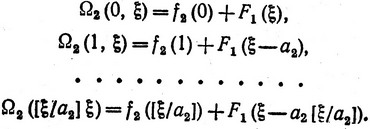
Наибольшая из этих величин как раз и есть F2 (ξ). Одновременно определяется также величина или величины 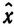 2 (ξ), для которых F2 (ξ) = Ω2 (
2 (ξ), для которых F2 (ξ) = Ω2 (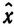 2, ξ).
2, ξ).
Отметим, что для определения F2 (ξ) необходимо знать только F1 (ξ - a2x2), причем число ξ - a2x2 есть целое неотрицательное число в силу сделанного ранее предположения о целочисленности aj. Но величины F1 (ξ) были вычислены ранее; поэтому нужно просто взять из них ту, которая соответствует числу ξ - a2x2.
Продолжая вычисления далее, определяем F3 (ξ) и 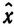 3 (ξ) для ξ = 0, 1, ..., b и т. д. вплоть до вычисления Fn-1 (ξ). Функцию Fn (ξ) необходимо вычислить только для ξ = b (Fn (b) = Z*). Значение (или значения)
3 (ξ) для ξ = 0, 1, ..., b и т. д. вплоть до вычисления Fn-1 (ξ). Функцию Fn (ξ) необходимо вычислить только для ξ = b (Fn (b) = Z*). Значение (или значения) 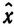 n (b) есть как раз то значение x*n, при котором получается максимум на последнем шаге, т. е. достигается Fn (b). Для нахождения x*1, x*2, ..., x*n-1, составляющих вместе с x*n оптимальное управление, следует использовать уже вычисленные значения
n (b) есть как раз то значение x*n, при котором получается максимум на последнем шаге, т. е. достигается Fn (b). Для нахождения x*1, x*2, ..., x*n-1, составляющих вместе с x*n оптимальное управление, следует использовать уже вычисленные значения 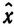 k (ξ). Так как величина x*n уже определена, остальные (n-1) переменные должны удовлетворять условию
k (ξ). Так как величина x*n уже определена, остальные (n-1) переменные должны удовлетворять условию
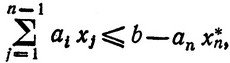
(3.14)
где теперь b - anx*n - заданное число (числа). Поэтому 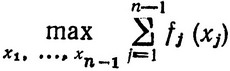 должен достигаться на множестве неотрицательных целых чисел, удовлетворяющих (3.14), т. е. Fn-1 (ξ) = Fn-1 (b - anx*n) (см. соотношение (3.5)), и значение (значения) x*n-1 при котором этот максимум достигается, есть
должен достигаться на множестве неотрицательных целых чисел, удовлетворяющих (3.14), т. е. Fn-1 (ξ) = Fn-1 (b - anx*n) (см. соотношение (3.5)), и значение (значения) x*n-1 при котором этот максимум достигается, есть
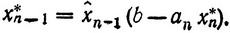
(3.15)
Так как значения 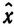 n-1 (ξ) уже вычислены, то следует из этих значений взять число, соответствующее ξ = b - anxn*. Точно так же находится x*n-2:
n-1 (ξ) уже вычислены, то следует из этих значений взять число, соответствующее ξ = b - anxn*. Точно так же находится x*n-2:

или в общем виде
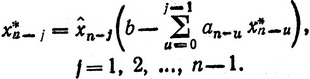
(3.16)
Как нетрудно догадаться, выдвинутое выше при формулировании задачи требование целочисленности aj гарантирует целочисленность аргументов функций Fk, что позволяет упростить процесс их вычисления.
На этом заканчиваются вычисления, позволяющие решить задачу (3.1), т. е. найти Z* и множество x1*, ..., x*n, образующих оптимальное управление. Отметим еще раз, что описанный вычислительный метод позволяет отыскать имеющиеся оптимальные решения. Однако зачастую очень трудно сделать.
В качестве иллюстрации метода динамического программирования рассмотрим простую задачу вида (3.1), в которой как ограничения, так и функция цели являются линейными. Заметим, что это не мешает продемонстрировать все особенности этого метода, поскольку в процессе решения мы должны только вычислять значения функции fj(xj) при заданных (целых) значениях xj, что не представляет особого труда сделать вручную для функций практически любого вида при наличии соответствующих таблиц или с помощью современных ЭВМ, у которых, как правило, имеются готовые подпрограммы вычисления различных функций. Итак, найдем
max Z = 2x1 + 3x2 + x3
при ограничении 0,4x1 + 0,8x2 + x3≤2.
Прежде всего представим ограничение в таком виде, чтобы все aj стали целыми:
2x1 + 4x2 + 5x3 ≤ 10.
Затем начнем вычислять функции F1(ξ) (3.12). В нашем случае ξ = 0, 1, 2, ..., 10, f1 (x1) = 2x1, a1 = 2. Поэтому величина [ξ/a1] = 0, 1, ..., 5. При ξ = 0 имеем только x1 = 0 и
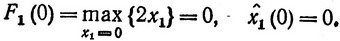
При ξ = 1 величина x1 заключена в пределах 0≤x1≤1/2, т. е. единственное целочисленное значение, которое может принимать x1, есть также x1 = 0, поэтому F1 (1) = 0 и 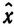 1 (1) = 0. Однако при ξ = 2 уже могут быть x1 = 0 и x1 = 1, т. е.
1 (1) = 0. Однако при ξ = 2 уже могут быть x1 = 0 и x1 = 1, т. е.
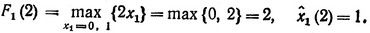
Рассуждая аналогично, получаем
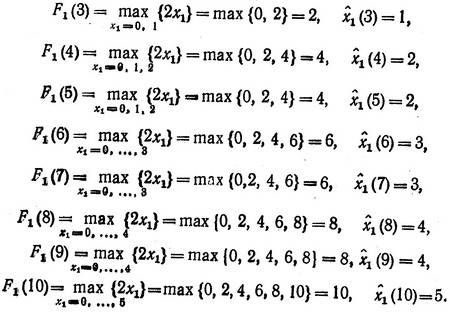
Таким образом, мы определили значения функции F1 (ξ) для всех возможных ξ и соответствующие им значения 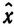 (ξ). Далее переходим к вычислению функции F2 (ξ) по формуле (3.13), используя уже известные значения функции F1 (ξ) для тех же значений ξ = 0, 1, ..., 10 (f2 (x2) = 3x2, a2 = 4).
(ξ). Далее переходим к вычислению функции F2 (ξ) по формуле (3.13), используя уже известные значения функции F1 (ξ) для тех же значений ξ = 0, 1, ..., 10 (f2 (x2) = 3x2, a2 = 4).
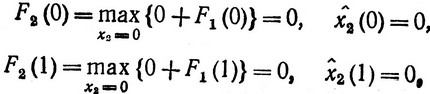
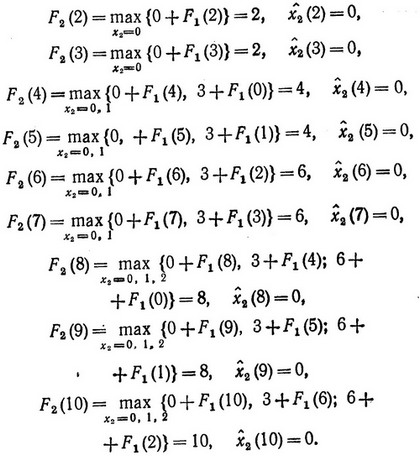
Функцию F3 (ξ) необходимо вычислить только для ξ = 10, и ее значение как раз определит max Z. Итак, для f3 = x3 и a3 = 5 согласно (3.11) имеем
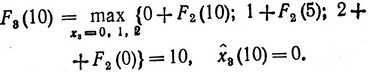
Значение 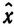 3 есть как раз то значение x*3, при котором получается максимум относительно переменной x3. Значение переменной x*2 определяем согласно (3.15):
3 есть как раз то значение x*3, при котором получается максимум относительно переменной x3. Значение переменной x*2 определяем согласно (3.15):
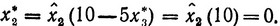
И наконец, имеем
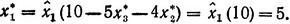
Таким образом, оптимальное решение (управление) есть x*1 = 5, x*2 = 0, x*3 = 0, и при этом функция цели достигает максимального значения Z* = 10. Вследствие крайней простоты условий задачи в правильности такого ответа нетрудно убедиться непосредственно.
Интересно провести сравнение вычислительного метода динамического программирования с прямым перебором допустимых решений (т. е. всех возможных наборов значений неотрицательных целых чисел xj, удовлетворяющих ограничению), для каждого из которых вычисляется функция цели, и из них выбирается тот набор, который обращает в максимум функцию цели.
Если все aj ≠ 1, то точное сравнение провести затруднительно. Поэтому рассмотрим лишь случай aj = 1, т. е. 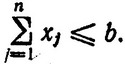 Нижней границей числа различных комбинаций, удовлетворяющих этому ограничению, будет число различных комбинаций целых чисел, обращающих это ограничение в строгое равенство. Оно равно числу способов, которыми можно разместить b одинаковых шаров в n ящиках. Это число способов есть число сочетаний из b + n - 1 элементов по b, которое равно
Нижней границей числа различных комбинаций, удовлетворяющих этому ограничению, будет число различных комбинаций целых чисел, обращающих это ограничение в строгое равенство. Оно равно числу способов, которыми можно разместить b одинаковых шаров в n ящиках. Это число способов есть число сочетаний из b + n - 1 элементов по b, которое равно
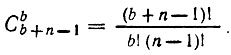
Если воспользоваться вычислительным методом динамического программирования, то для вычисления всех Fk (ξ) при заданном k необходимо вычислить

значений. Для того чтобы вычислить функции Fk (ξ) для (n-1) шагов, соответственно требуется провести число вычислений в (n-1) раз большее. Однако для последней функции Fn (ξ) необходимо знать лишь значение Fn(b); поэтому потребуется провести только b + 1 вычисление. Таким образом, общее число вычислений равно:
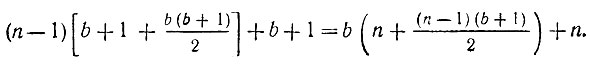
Нетрудно убедиться для различных b и n, что при прямом переборе решений требуется выполнить во много раз дольше вычислений, причем эта разница возрастает с ростом n.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'