
§ 2. Экономическая интерпретация задачи линейного программирования
Экономическое истолкование задачи линейного программирования целесообразно дать на примере.
Допустим,что некоторое предприятие согласно своему производственному профилю в разных количествах может выпускать n различных видов изделий, причем изделий первого вида x1 единиц, второго вида x2 единиц и т. д., изделий n-го вида xn единиц. Предприятию отпускается m различных видов сырья в количествах b1, b2, ..., bm для изготовления этих n видов изделий. Обозначим через a11 количество сырья b1, которое идет на изготовление одного изделия первого вида, через a12 - количество сырья b1, которое идет на изготовление одного изделия второго вида, и т. д. Таким образом, aij есть количество i-го вида сырья, которое идет на изготовление одного изделия j-го вида. Некоторые из чисел aij, конечно, могут быть равны нулю, некоторые изделия xj в данное время могут не выпускаться, т. е. в этом случае xj = 0; однако ни aij, ни xj не могут быть отрицательными.
Сравнивая затраты каждого вида сырья на изготовление всех изделий с имеющимся количеством сырья, приходим к системе неравенств
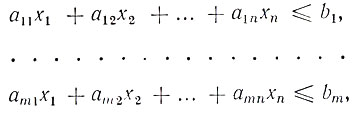
(1.4)
где x1 ≥ 0, x2 ≥ 0, ..., xn ≥ 0.
Эти неравенства выражают тот факт, что затраты сырья не могут превосходить его наличия.
Далее обозначим через c1 прибыль от производства одной единицы продукции первого вида, c2 - прибыль от продукции второго вида и т. д. Суммарная прибыль от производства всех изделий составит f = c1x1 + c2x2 + ... + cnxn. Требуется построить такой план выпуска продукции, который обеспечит производству максимальный доход.
Итак, сформулированная таким образом задача планирования производства непосредственно приводит нас к задаче линейного программирования.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'