Глава 41. Трансцендентное число "Пи"

"Лицо Пи было скрыто маской. Все понимали, что сорвать ее, оставшись при этом в живых, не сможет никто. Сквозь прорези маски пронзительно, безжалостно, холодно и загадочно смотрели глаза",- так писал в своей книге "Кошмары выдающихся личностей" Бертран Рассел.

Отношение длины окружности к ее диаметру, которое древние греки обозначили буквой π ("пи"), возникает во многих ситуациях, не имеющих никакого отношения к окружностям. Английский математик Август де Морган назвал как-то "пи" "...загадочным числом 3,14159..., которое лезет в дверь, в окно и через крышу". Приведем лишь один пример. Рассмотрим множество целых положительных чисел. Если из них случайным образом выбрать два числа, то какова вероятность того, что выбранные числа не будут иметь общего делителя? Ответ неожидан: искомая вероятность равна 6/π². Тем не менее именно то обстоятельство, что я связано с окружностью, сделало его наиболее известным представителем бесконечного класса трансцендентных чисел.

Что такое трансцендентное число? По определению трансцендентным называют число, которое не является корнем никакого алгебраического уравнения с рациональными коэффициентами. Квадратный корень из 2 - число иррациональное, но это - "алгебраическое иррациональное" число, потому что √2 есть корень квадратного уравнения х² - 2 = 0. Число я не может быть корнем ни одного алгебраического уравнения с рациональными коэффициентами, оно получается в результате некоторого предельного перехода. Дробная часть десятичной записи числа π, как и у всех иррациональных чисел, бесконечна и непериодична.

Ни одна дробь с целым числителем и знаменателем не может быть в точности равной π, но существует много простых дробей, которые дают исключительно хорошее приближение числа я. Самая замечательная из таких дробей была найдена еще в V веке до нашей эры знаменитым китайским астрономом Цю Шуньши. На Западе ее открыли лишь тысячу лет спустя. Получить ее можно с помощью числового фокуса. Напишем по два раза первые три нечетных числа: 1, 1, 3, 3, 5, 5. Три последних числа сделаем числителем, а три первых - знаменателем дроби: 355/113. Трудно поверить ,(а между тем это чистейшая правда), что эта дробь позволяет вычислить я с точностью до седьмого знака. Приближенные значения я можно получать и с помощью корней из различных чисел. Так, древние заменяли я числом √10 (3,162...). Еще лучшее приближение дает ³√31(3,1413...). Для любителей нумерологии заметим, что первые две цифры десятичного разложения π - это те самые тройка и единица, которыми записано число 31. Длина ребра куба объемом 31 см³ отличается от я меньше чем на 0,001 см. Неплохим приближением к я может служить сумма √2+√3, равная 3,146...

Первые попытки вычислить точное значение я тесно связаны с попытками решить классическую проблему квадратуры круга. Можно ли, пользуясь только циркулем и линейкой, построить квадрат, площадь которого была бы в точности равна площади данного круга? Если бы мы могли представить я в виде рациональной дроби или корня линейного или квадратного уравнения, то с помощью циркуля и линейки нам нетрудно было бы построить отрезок прямой, длина которого была бы в точности равна половине длины окружности. Отсюда уже совсем просто было бы получить квадратуру круга: для этого достаточно построить прямоугольник, у которого одна сторона равна радиусу окружности, а другая - половине ее длины. Площадь такого прямоугольника равна площади круга, а превратить его в равновеликий квадрат легко. Наоборот, если бы задача о квадратуре круга была разрешима, то это бы означало, что мы можем построить отрезок прямой, длина которого была бы в точности равна π. Однако существуют совершенно строгие доказательства трансцендентности числа я и невозможности построения с помощью циркуля и линейки отрезка, длина которого выражается трансцендентным числом.

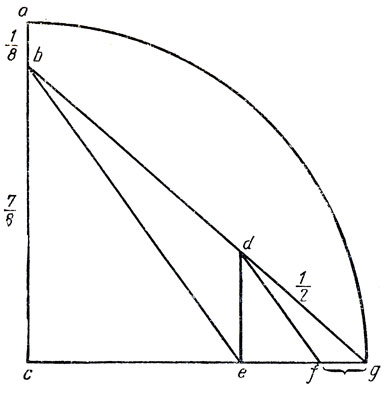
Рис. 212. Как построить отрезок прямой, длина которого отличается от π меньше чем на 0,0000003

Предлагались сотни способов приближенного построения π; одно из наиболее точных построений основано на уже упоминавшемся нами приближенном представлении числа π в виде рациональной дроби, найденном китайским астрономом. Проведем в четверти единичного круга несколько линий (рис. 212) так, чтобы отрезок bc был равен ⁷/₈ радиуса, dg-¹/₂, отрезок de был параллелен отрезку ас, а df - параллелен отрезку bc. Тогда, как легко видеть, расстояние fg равно ¹⁶/₁₁₃, или 0,1415929... Поскольку ³⁵⁵/₁₁₃ = 3 + ¹⁶/₁₁₃, отложим отрезок втрое длиннее радиуса, продолжим его на расстояние fg и получим новый отрезок, длина которого отличается от я меньше чем на одну миллионную.

Тысячи людей, бившихся над решением задачи о квадратуре круга, были уверены, что им удалось построить отрезок, длина которого в точности равна я, но никто из них не смог превзойти английского философа Томаса Гоббса, в котором высокий интеллект сочетался с глубочайшим невежеством. Во времена Гоббса даже образованного англичанина не обучали математике, поэтому Гоббс до сорока лет не заглядывал в "Начала" Евклида. Впервые в жизни прочитав формулировку теоремы Пифагора, он воскликнул: "Боже, но это невозможно!" Однако затем шаг за шагом он проследил все доказательство и убедился в его правильности. С тех пор и до конца своей долгой жизни Гоббс с пылом влюбленного все свои помыслы безраздельно отдавал геометрии. "Геометрия чем-то напоминает вино",- писал он позднее. Рассказывают, что, когда у него под рукой не оказывалось более подходящей поверхности, Гоббс имел обыкновение чертить геометрические фигуры у себя на ноге или на простынях.

Если бы Гоббс так и остался любителем, то его последующие годы протекали бы более спокойно, однако чудовищное самомнение привело к тому, что он возомнил себя способным на великие математические открытия. В 1665 году, в возрасте 67 лет, он выпустил в свет на латинском языке книгу под названием "De corpore" ("О телах"), в которой, помимо прочего, излагался остроумный метод решения задачи о квадратуре круга. Его метод и в самом деле позволял найти превосходное приближение числа я, но Гоббс считал свой метод точным. Джон Валлис, знаменитый английский математик и специалист по криптографии, изложил ошибки Гоббса в памфлете. Так началась самая продолжительная, нелепейшая и бесполезнейшая словесная перепалка, в которой когда-либо участвовали два блестящих ума. Спор длился почти четверть века, обе стороны перемежали в своих публичных выступлениях едкий сарказм грубой бранью. Валлис продолжал бессмысленную "драку" отчасти ради собственного развлечения, отчасти для того, чтобы выставить Гоббса в смешном свете и тем самым очернить его религиозные и политические убеждения, которые Валлис порицал.

На первые нападки Валлиса Гоббс ответил переизданием своей книги на английском языке с добавлением, озаглавленным "Шесть уроков профессорам математики..." (думаю, что читатели простят мне, если я не стану приводить полностью характерные для XVII века длиннейшие заглавия). Валлис парировал выступление своего противника, опубликовав "Поправку, в которой нуждаются познания мистера Гоббса в одной школьной дисциплине, не говоря уже о его "Шести уроках"". В ответ на это Гоббс разразился "Замечаниями об абсурдной геометрии, деревенском языке, церковной политике в Шотландии и дремучем невежестве Джона Валлиса". Тот не заставил себя ждать и выпустил труд под названием "Hobbiani Puncti Dispunctio, или опровержение замечаний мистера Гоббса". Несколько позднее (опубликовав анонимно в Париже абсурдный метод решения задачи об удвоении куба) Гоббс писал: "Либо я сошел с ума, либо все они (профессора математики) не в своем разуме. Третьего быть не может, разве что они скажут, будто мы все рехнулись".

"Довод моего противника не нуждается в опровержении,- был ответ Валлиса,- ибо если он сошел с ума, то вряд ли его можно убедить доводами разума. Если же мы все сошли с ума, то мы не в состоянии даже попытаться опровергнуть его довод".

С небольшими перерывами борьба продолжалась до самой смерти Гоббса, последовавшей на 91-м году жизни. "Мистер Гоббс всегда был далек от мысли бросать кому-нибудь вызов,- писал Гоббс в одной из своих филиппик против Валлиса (и действительно, в отношениях с другими людьми Гоббс был крайне робок),- но, бросив ему вызов, вы убедитесь, что перо его не уступит в остроте вашему. Все сказанное вами состоит наполовину из лжи, наполовину из брани. Оно ничем не отличается от того зловония, которое испускает старая кляча, если, обкормив ее овсом, мы слишком туго затянем подпругу. Я кончил. Я уделил вам достаточно внимания и не намерен возвращаться к этому неприятному для меня занятию вновь..."

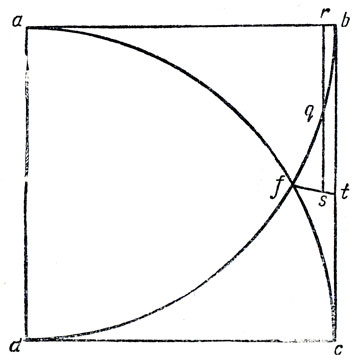
Рис. 213. Один из способов решения задачи о квадратуре круга, принадлежащий Гоббсу

Мы не будем подробно обсуждать здесь то, что Валлис назвал удивительной "неспособностью" Гоббса "научиться тому, чего он не знает". Достаточно сказать, что Гоббс опубликовал около десятка различных способов решения задачи о квадратуре круга. Первое и лучшее решение показано на рис. 213. Внутри единичного квадрата проведены дуги ас и bd. Каждая из них равна четверти окружности единичного радиуса. Точка q делит дугу bf пополам. Проведем отрезок rq, параллельный стороне квадрата, и продолжим его за точку q на расстояние, равное rq (то есть отложим на продолжении отрезок qs = rq). Проведем отрезок fs и продолжим его до пересечения со стороной квадрата в точке t. Гоббс утверждал, что отрезок bt в точности равен дуге bf, а так как дуга bf составляет ¹/₁₂ единичной окружности, то число я равно шестикратной длине отрезка bt. При этом значение я получается равным 3,1419...

Рис. 214. Титульный лист одной из книг Гоббса, содержащей 'решение' задачи о квадратуре круга

Одну из главных причин всех затруднений Гоббса понять нетрудно. Он никак не мог привыкнуть к мысли о том, что точки, линии и поверхности можно рассматривать абстрактно как геометрические объекты, размерность которых меньше трех. "По-видимому, он так и ушел в могилу,- пишет в книге "Ссоры авторов" Исаак Дизраэли,- с твердым убеждением, что поверхности обладают и глубиной, и толщиной, несмотря на все возражения геометров, выслушанные им при жизни". Гоббс представляет собой классический пример человека выдающихся способностей, вступившего в область яауки, для которой он плохо подготовлен, и растратившего всю энергию на решение пустых псевдонаучных вопросов.

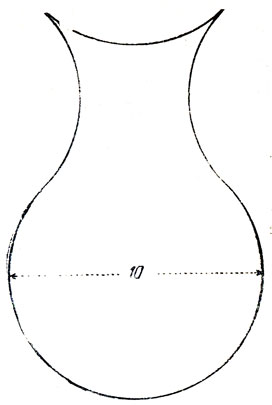
Рис. 215. Скольким квадратным единицам равна площадь этой фигуры?

Хотя невозможность квадратуры круга строго доказана, задача о квадратуре фигур, ограниченных дугами окружности, часто бывает вполне разрешимой. Именно это обстоятельство все еще пробуждает ложные надежды у "квадратурщиков". Интересный пример такой квадрируемой фигуры показан на рис. 215. Контур нижней части этой вазы образован дугой в ³/₄ окружности радиусом 10 см. Верхняя половина ограничена тремя четвертушками той же окружности. Как быстро сможет читатель назвать с точностью до последнего десятичного знака длину стороны квадрата, имеющего площадь, равную площади этой фигуры?

Близкими родственниками "квадратурщиков" были вычислители π - те, кто порой затрачивал целые годы для того, чтобы вручную найти новые знаки в десятичном разложении π, оставив позади все ранее проведенные вычисления. Для этого использовали бесконечные ряды или произведения, сходящиеся к π. Одно из простейших выражений для π открыл Валлис:

В числителях дробей по два раза повторяются последовательные четные числа. (Отметим случайное сходство между первыми пятью знаменателями и цифрами в рациональном приближении числа π, открытом китайским астрономом!) Несколько десятилетий спустя великий Лейбниц открыл другую изящную формулу:

Самым неутомимым вычислителем я был английский математик Уильям Шенкс. Более 20 лет жизни он посвятил вычислению 707 знаков числа π. К сожалению, несчастный Шенкс ошибся в пятьсот двадцатом знаке, и все последующие цифры в полученном им выражении неверны. (Ошибку обнаружили лишь в 1945 году, поэтому семисотсемизначное разложение Шенкса и поныне еще можно встретить во многих книгах.) В 1949 году электронно-вычислительная машина "ЭНИАК", проработав в течение 70 часов, вычислила более 2000 знаков числа π. Позднее с помощью другой вычислительной машины, проработавшей всего лишь 13 минут, были вычислены 3000 знаков π. В 1959 году одна вычислительная машина в Англии и другая во Франции вычислили 10 000 десятичных знаков π.

Самое странное в найденных Шенксом 707 знаках я заключается в том, что эти знаки "свысока" смотрят на цифру 7: если каждая из остальных цифр, как и должно быть, встречается среди первых 700 знаков около 70 раз, то семерка появляется лишь 51 раз. "Если бы все циклометристы и апокалипсисты объединили свой разум,- писал де Морган,- и до тех пор, пока они не придут к единому мнению относительно причин этого явления, не печатали бы ни единой строки, то они бы заслужили признательность всего человечества". Спешу добавить, что после того, как все 707 первых знаков π были вычислены верно, недостающие семерки заняли подобающее им место и справедливость была восстановлена. Математики-интуиционисты придерживаются того мнения, что утверждение об "истинности или ложности" любого высказывания лишено смысла, если вы не можете подтвердить или опровергнуть это высказывание, и всегда приводят пример такого высказывания: "В десятичном разложении числа я встречаются три семерки подряд". Ныне мы с полной уверенностью можем утверждать, что высказывание "В десятичном разложении числа π встречаются подряд пять семерок" истинно. Среди недавно полученных десятичных знаков для я были обнаружены не только неоднократно повторяющиеся тройки всех цифр от 0 до 9, но и несколько групп из 4 семерок (и совершенно неожиданная очередь из 6 девяток).

До сих пор я благополучно выдерживало все статистические испытания на случайность. Это кажется непонятным тем, кто полагает, что у столь простой и изящной кривой, как окружность, должно было бы быть менее дикое отношение между "обхватом" и поперечником, но большинство математиков твердо уверены в том, что среди цифр десятичного разложения я никогда не будет обнаружено никакого порядка. Разумеется, эти числа не случайны в том смысле, что они определяют число я, но в этом же смысле не случаен и миллион "случайных" цифр в таблицах так называемых "случайных чисел". Они также представляют некоторое число, к тому же целое.

Если верно, что цифры в десятичном разложении я случайны, то мы, по-видимому, с полным основанием можем сформулировать парадокс, в какой-то мере аналогичный парадоксу стада обезьян, которые, просидев достаточно долго за пишущими машинками, смогут напечатать все пьесы Шекспира. Стифен Барр заметил, что если не ставить пределов точности измерения длины стержней, то с помощью двух стержней, не делая на них никаких зарубок или меток, можно в принципе передать содержание всей "Британской энциклопедии". В самом деле, длина одного стержня принимается за единицу (эталон) длины. Длина другого выбирается так, чтобы она отличалась от единичной на величину, выражающуюся очень длинной десятичной дробью. Цифрами десятичной дроби закодирован текст "Британской энциклопедии": различным числам (в десятичной записи которых нет нуля) сопоставлены слова и знаки пунктуации, встречающиеся во всех томах энциклопедии от "А" до "Z"; нуль использован для разделения кодовых чисел. Ясно, что таким образом всю "Британскую энциклопедию" можно закодировать одним, хотя и невероятно длинным числом. Поставив перед этим числом запятую и приписав слева единицу, мы получим длину второго стержня Барра.

При чем же здесь π? А вот при чем: если цифры в десятичном разложении я действительно распределены случайно, то где-то в их бесконечной последовательности должен встретиться отрезок, содержащий в закодированном виде всю "Британскую энциклопедию", а также любую книгу, которая была, будет или могла быть написана.

В 1961 году машина ИБМ-7090 вычислила я с точностью до 100 625 знаков. Программа была составлена Дэниэлом Шенксом (не имеющим никакого отношения к Уильяму Шенксу; это лишь одно из тех странных совпадений, которыми изобилует история числа π) и Джоном У. Ренчем младшим. Машинное время составило 8 час 1 мин; еще 42 мин потребовалось для того, чтобы перевести результат из двоичной в десятичную форму. Вычисление нескольких тысяч знаков я в настоящее время стало популярным средством проверки новых вычислительных машин и обучения молодых программистов. "Загадочное и чудесное π,- пишет в своей книге "Что мы знаем о больших числах" Филипп Дж. Дэвис,- стало чем-то вроде покашливания, которым вычислительные машины прочищают горло".

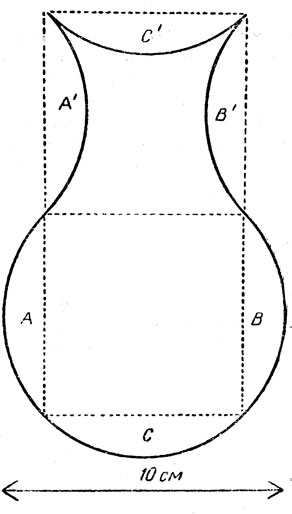
Рис. 216. Как 'квадрировать' вазу

Читателю предлагалось найти сторону квадрата, равновеликого (по площади) фигуре, похожей на вазу (рис. 216) и ограниченной дугами окружности диаметром 10 см. Ответ: сторона квадрата также равна 10 см. Если пунктирные линии провести так, как показано на рисунке, то станет видно, что сегментами А, В и С можно заполнить "лунки" А', В' и С, при этом образуются два квадрата общей площадью 100 см². На рис. 217 показано, как разрезать вазу всего лишь на три части так, чтобы из них можно было сложить квадрат 10×10 см.

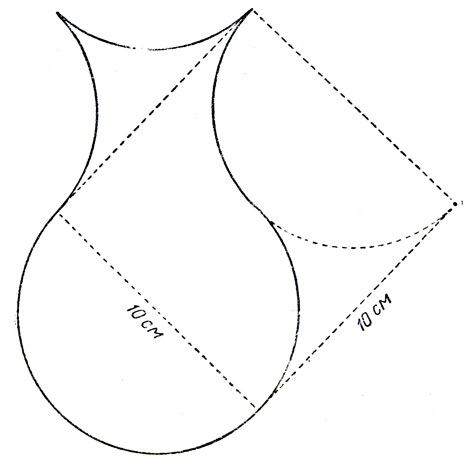
Рис. 217. Квадрирование вазы разрезанием ее на три части