Глава 36. Теория групп и косы

Понятие "группы" - одно из основных понятий современной алгебры, охватывающее общие свойства самых разнообразных объектов различной природы и служащее неоценимым средством исследования в физике,- Джеймс Р. Ньюмен сравнивал с улыбкой Чеширского Кота^*: когда Чеширский Кот (алгебра в том виде, как ее обычно преподают в школе) исчезает, остается только его абстрактная улыбка. Но улыбка подразумевает нечто веселое, занимательное. Может быть, теория групп покажется нам менее загадочной, если мы не будем воспринимать ее слишком серьезно.

^* (Чеширский Кот - один из персонажей известной сказки Льюиса Кэррола "Алиса в'Стране Чудес".- Прим. перев.)

Трое программистов - Эймз, Бейкер и Кумбс - хотят решить, кому из них платить за пиво. Разумеется, они могли бы бросить монетку, но предпочитают случайный выбор, основанный на следующей игре - блуждании по некоторой сети линий. На листе бумаги проведены три вертикальные линии (назовем их основой). Один из программистов, держа лист так, чтобы его друзья не видели, что он делает, обозначает эти линии наугад буквами А, В и С (181, а). Верхний край листа он загибает так, чтобы буквы не были видны. Второй программист наугад проводит ряд горизонтальных линий (назовем их утком), каждая из которых соединяет какие-нибудь две вертикальные линии (рис. 181, б). Третий программист добавляет, еще несколько горизонтальных линий, а у одной из вертикальных линий снизу ставит букву X (рис. 181, в).

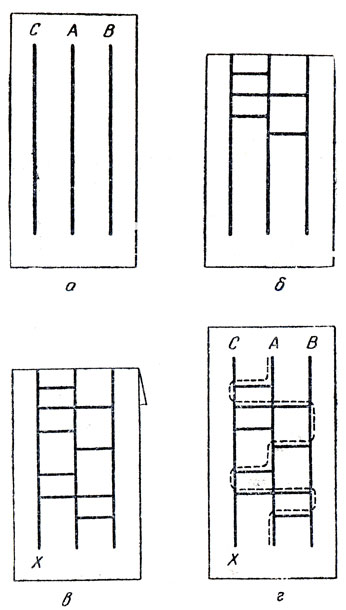
Рис. 181. Блуждание по линиям 'основы' и 'утка'

Лист бумаги разворачивают. Эймз ставит свой палец в верхнюю точку линии А и начинает обводить ее сверху вниз. Дойдя до начальной или конечной точки линии утка (если точка пересечения вертикальной линии с линией утка лежит внутри горизонтального отрезка, Эймз ее пропускает и следует дальше), он поворачивает и проходит всю эту линию до другого ее конца, после чего снова поворачивает и продолжает спускаться вниз до тех пор, пока снова не встретит начальную или конечную точку другой линии утка. Так продолжается, пока он не достигнет нижней точки какой-нибудь вертикальной прямой. Если его путь (на рис. 181, г он показан пунктирной линией) заканчивается не в точке X, то за пиво платит не он. Затем точно таким же способом по сети прямых путешествуют Бейкер и Кумбс. Путь Бейкера заканчивается в точке X, поэтому за пиво приходится платить ему. Каким бы ни было число линий основы (вертикальных прямых), независимо от того, как проведены линии утка (горизонтальные прямые), пути игроков всегда заканчиваются на различных прямых, и никакие два маршрута никогда не приводят к одной и той же линии.

При более подробном рассмотрении этой игры выясняется, что в основе ее лежит одна из простейших групп - так называемая, группа перестановок трех элементов. Что же такое группа? Это некая абстрактная структура, состоящая из множества элементов (a, b, с, ...), относительно природы которых не делается никаких предположений, с единственной бинарной операцией (ее мы обозначим символом ○), сопоставляющей каждой паре элементов множества некоторый третий элемент. Чтобы такая структура составляла группу, должны выполняться следующие четыре условия:

1. Каждой паре элементов множества операция ставит в соответствие некоторый элемент того же множества. Это свойство носит название "замкнутости" множества относительно операции.
2. Операция подчиняется "ассоциативному закону":
   (а○b)○с = а○(b○с).
3. Существует элемент e (называемый "единицей"), такой, что
   а○e = e○а = а.
4. Для каждого элемента а существует обратный элемент а', такой, что
   а○а' = а'○а = e.

Если помимо только что названных четырех условий операция подчиняется еще и коммутативному закону:

то группа называется коммутативной, или абелевой.

Целые числа - положительные, отрицательные и нуль - образуют группу относительно сложения (это наиболее известный пример группы). Множество целых чисел замкнуто относительно сложения (прибавить 2 к 3, а затем к 4 - то же самое, что прибавить 2 к сумме чисел 3 и 4); "единицей" группы служит 00 а элементом, обратным (или, как говорят еще, противоположным) целому положительному числу,- то же число; взятое со знаком минус. Группа целых чисел относительно сложения - абелева (2 + 3 = 3 + 2). Если в качестве операции выбрать деление, то целые числа не будут образовывать группы: поделив 5 на 2, мы получим 272, а это число не принадлежит множеству целых чисел.

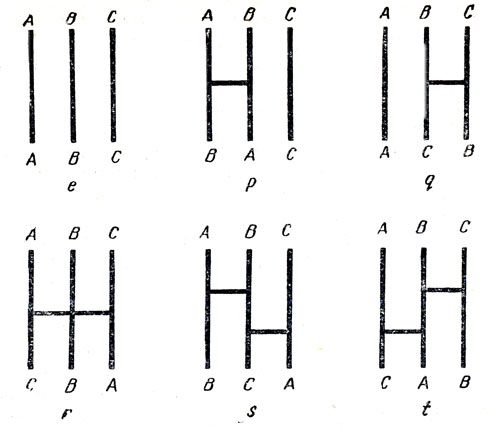
Рис. 182. Шесть элементов группы, возникающей в задаче о блуждании по сети линий

Выясним теперь, с какой группой связана задача о блуждании по линям "утка и основы". Шесть основных "преобразований" - элементов нашей конечной группы - изображены на рис. 182. Преобразование p "переводит стрелку": начав двигаться по прямой A, вы закончите свой путь на прямой В и, наоборот, начав путь по прямой В, вы в конце концов окажетесь на прямой А (зато, попав на прямую С, вы останетесь на ней до конца). Преобразования q, r, s и t задают другие перестановки начал и концов различных путей. Преобразование e в действительности ничего не меняет, но математики все равно называют его "преобразованием" в том же смысле, в каком пустое множество, не содержащее ни одного элемента, называют множеством. Для того чтобы выполнить преобразование e, не нужно проводить вообще никаких горизонтальных линий; это "тождественное" преобразование, которое в действительности ничего не преобразует. Шесть элементов группы соответствуют шести различным перестановкам трех символов. Групповая операция, обозначенная символом ○, заключается в последовательном выполнении одного преобразования за другим, в добавлении к горизонтальной линии одного преобразования горизонтальной линии следующего преобразования.

Нетрудно проверить, что все свойства группы соблюдены. Множество преобразований замкнуто относительно операции "добавление горизонтальных линий" потому, что какую бы пару его элементов мы ни взяли, концы линий A, В и С окажутся переставленными так же, как и в результате применения к прямым A, В и С одного из шести преобразований. Например, p○t = r, так как, выполнив вслед за преобразованием р преобразование t, мы получим в точности такое же расположение концов линий A, В и С, какое получается при действии лишь одного преобразования r. Добавление горизонтальных линий, очевидно, ассоциативно (то есть, имея три горизонтали, мы можем сначала построить две первые, а затем пристроить к ним третью, но можем действовать и иначе: сначала провести две последние, посмотреть, как выглядит их "сумма", и добавить ее к первой горизонтали; в том и в другом случае результат будет одинаков). Если не проводить никаких горизонталей, то получится единичное, или тождественное, преобразование. Элементы р, q и r совпадают с обратными им элементами, а каждый из элементов s и t обратен другому. (Выполнить вслед за одним преобразованием другое, ему обратное, все равно, что вообще не проводить новых горизонтальных линий.) Полученная группа неабелева (например, если выполнить сначала преобразование q, а потом преобразование p, то результат получится совсем иным, чем в том случае, когда сначала выполняется преобразование р и лишь затем - преобразование q).

Рис. 183. Результаты последовательного выполнения двух преобразований из группы, возникающей в задаче о блуждании по сети линий

Полное описание строения этой группы видно из рис. 183. Что получится, если вслед за преобразованием r проделать преобразование s? Найдем букву r среди букв, выписанных слева от таблицы, и букву 5 среди букв, выписанных сверху. На пересечении r-й строки и s-го столбца стоит буква р. Иначе говоря, добавив к горизонтальным линиям преобразования r горизонтальные линии преобразования s, мы получим такую же перестановку нижних концов вертикальных линий А, В и С, какая возникнет, если провести горизонтальные линии одного лишь преобразования р. Эта чрезвычайно простая группа возникает во многих местах. Например, если обозначить тремя различными буквами вершины равностороннего треугольника, а затем произвести над ним все повороты и отражения, в результате которых он совмещается с самим собой, то окажется, что различных преобразований имеется только шесть и они образуют в точности такую же группу, как только что описанная.

Не обязательно вникать в тонкости теории групп, чтобы интуитивно понять, что, блуждая по сети, никакие два игрока не могут закончить свой путь на одной и той же вертикали. Вообразим, что три вертикальные линии - это просто-напросто три веревки. Каждый раз, проводя горизонтали, мы как-то переставляем нижние концы вертикалей, но точно такого же результата мы достигнем, если перевьем две веревки так, как это делают с прядями волос при заплетании косы. Ясно, что, как бы вы ни заплетали косу и какой бы длинной она ни была, дойдя до ее конца, вы всегда сможете различить все три пряди.

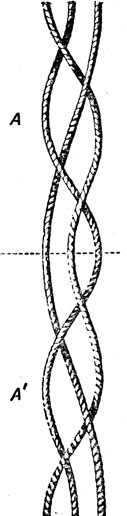
Рис. 184. Коса А - зеркальное отражение косы А'

Представим себе, что и мы заплетаем девичью косу из трех прядей. Схематически последовательные перестановки прядей можно изобразить в виде сети (аналогичной той, которой мы пользовались в задаче о трех программистах), но при этом останется неясным, какие пряди оказываются сверху, а какие - снизу. Пригодна ли теория групп для описания действий, производимых нами при заплетании косы, с учетом этого усложняющего топологического фактора? Оказывается, вполне пригодна. Впервые это доказал немецкий математик Эмиль Артин. В его изящной теории кос элементами группы (их бесконечно много) служат "схемы переплетения", а групповой операцией, так же как в задаче о блуждании по сети линий,- последовательное применение одной схемы за другой. Роль единичного элемента играет схема переплетения, состоящая из трех отдельных вертикалей - не переплетенных между собой прядей ("косу еще не начинали заплетать"). Чтобы найти элемент группы, обратный какой-нибудь схеме переплетения, нужно просто взять зеркальное отражение этой схемы. На рис. 184 показана простенькая схема, взятая вместе с обратной ей схемой. Если косу заплести сначала по "прямой", а потом по обратной схеме, то достаточно очевидно, что результат будет топологически эквивалентен заплетанию по единичной схеме: стоит лишь слегка потянуть за конец косы, изображенной на рис. 184, как все ее пряди расплетутся и выпрямятся. (Многие фокусы с распутыванием шнурков и веревочек основаны именно на этом небезынтересном групповом свойстве. Об одном из наиболее эффектных фокусов такого рода мы рассказали в главе 22.) В своей теории кос Артин не только впервые произвел классификацию всех мыслимых типов кос, но и предложил метод, позволивший узнавать, эквивалентны топологически или нет любые две сколь угодно сложные схемы переплетения.

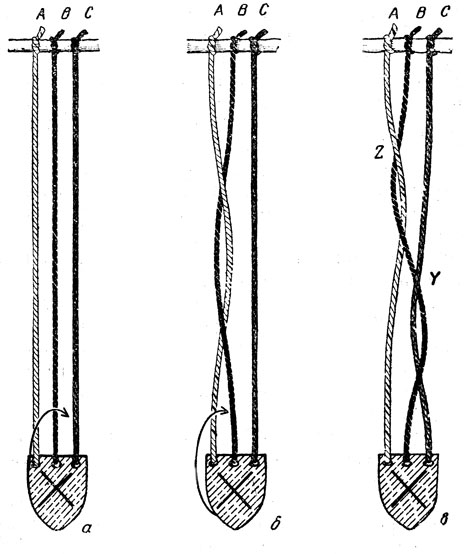
Рис. 185. Полный оборот подвески а по стрелке порождает косу б. Перевернув подвеску по стрелке еще раз, мы получим косу в.

Теория кос имеет самое непосредственное отношение к необычной игре, изобретенной все тем же датским поэтом, писателем и математиком Питом Хейном. Вырежьте из плотного картона кусочек в форме геральдического щита (рис. 185). Этот кусочек мы будем называть подвеской. Поскольку нам понадобится различать стороны подвески, их лучше всего раскрасить в разные цвета или одну из сторон пометить буквой X. У прямого края подвески проделайте три отверстия и, пропустив в каждое из них по отрезку тяжелого, но гибкого шнура длиной около 60 см, завяжите шнурки узлом (великолепно подходит для этих целей крученый шнур, из которого делают пояса). Другой конец каждого шнура привяжите к какому-нибудь неподвижному предмету, например к спинке стула.

Подвеска, как нетрудно видеть, может совершать полные обороты шестью различными способами: ее можно поворачивать на 360° вокруг вертикальной оси; поворачивать вокруг прямого края на себя или от себя, продевая ее между шнурами А и В; поворачивать также вокруг прямого края на себя или от себя, но продевать при этом между шнурами В и С. Во всех шести случаях получаются разные косы. Коса, которая "заплетается" при пропускании подвески между шнурами В и С, показана на рис. 185,6. Возникает вопрос, можно ли расплести эту косу, продевая подвеску между шнурами подобно ткацкому челноку и все время держа ее в плоскости рисунка - так, чтобы сторона, помеченная буквой X, была обращена к зрителю, а острый "носик" смотрел на вас (предполагается, что, читая, вы держите книгу на столе перед собой)? Оказывается, что сделать это невозможно, но стоит вам лишь перекинуть подвеску на один оборот любым из шести возможных способов, как вы получите косу, для расплетания которой достаточно, не поворачивая, продеть подвеску определенным образом между шнурами.

Поясним сказанное на примере. Предположим, что, поворачивая подвеску на 360° во второй раз, мы пропустили ее между шнурами А и В в направлении, указанном на рис. 185,6 стрелкой, и получили косу, изображенную на рис. 185,0. Чтобы расплести эту косу, не раскручивая подвески, нужно сначала оттянуть на себя шнур С в точке, отмеченной буквой Y, и пропустить под ним подвеску справа налево. После этого снова отпустим все шнуры и, оттянув на себя шнур А в том месте, которое обозначено буквой Z, пропустим под шнуром подвеску слева направо. В результате коса полностью расплетется.

Следующая удивительная теорема справедлива для кос, заплетенных из любого числа прядей, большего двух. Все косы, получающиеся при четном числе переворачиваний подвески (каждое переворачивание разрешается производить в любом направлении как на себя, так и от себя), всегда можно расплести, действуя подвеской как ткацким челноком, без новых поворотов ее; если же коса получилась оттого, что подвеска совершила нечетное число полных оборотов, то расплести ее без дополнительных оборотов подвески никогда не удастся.

Хейн впервые услышал об этой теореме в начале тридцатых годов на одном семинаре в Институте теоретической физики Нильса Бора, когда П. Эренфест обсуждал ее в связи с какой-то проблемой квантовой теории. С помощью ножниц супруги Бора и нескольких веревочек, привязанных к спинке стула, Хейну и другим участникам семинара удалось найти доказательство этой теоремы. Позднее Хейну пришло в голову, что вращающееся тело и окружающая его вселенная входят в задачу симметрично, поэтому симметричную модель можно было бы построить очень просто, привязав по подвеске к каждому концу шнура. Имея такую симметричную модель, можно вдвоем играть в топологическую игру. Каждый участник берет свою подвеску; между подвесками протянуты три шнура. Один из игроков заплетает косу, а второй, расплетая ее, засекает необходимое для этого время, затем игроки меняются ролями. Тот, кто расплетет косу быстрее, считается победителем.

Теорема о четном и нечетном числе поворотов подвески, очевидно, применима и к этой игре. Начинающим рекомендуется ограничиться косами, при заплетании которых подвеска совершает два полных оборота, и лишь потом, попрактиковавшись и набив руку, переходить к более сложным косам четного порядка. Хейн назвал свою игру "танглоид". В течение ряда лет она была очень популярна в Европе.

Почему между четным и нечетным числом полных оборотов подвески существует такое различие? На этот - весьма непростой вопрос трудно ответить, не вдаваясь более глубоко в теорию групп. Некоторое представление о причинах такого различия можно получить, заметив, что два поворота в противоположных направлениях - это то же самое, что ни одного поворота. Если два оборота почти противоположны и отличаются только тем, что при совершении их подвеска была пропущена между различными парами шнуров, то косу можно расплести, продев подвеску между шнурами так, чтобы уничтожить это различие. Пользуясь теорией кос, можно доказать, что при нечетном числе оборотов подвески пряди распутать нельзя.

Рис. 186. Три задачи на расплетание кос

Заплетать косы, поворачивая подвеску наугад четное число раз, а затем быстро расплетать их - занятие увлекательное. На рис. 186 показаны три простые косы, каждая из которых заплетена лишь двумя полными оборотами подвески. Косу в случае а получили, дважды пропустив подвеску между шнурами В и С (оба раза от себя); в случае б - продев подвеску между шнурами В и С от себя, а затем между шнурами А и В в обратном направлении. Коса в случае в заплелась оттого, что подвеску два раза повернули слева направо вокруг вертикальной оси. Читателю предоставляется самому найти лучший способ расплетания какой из этих кос.

При изготовлении "реквизита" для танглоида подвеску лучше вырезать не из картона, а из деревянной дощечки или пластика. Вместо трех отдельных шнуров Хейн рекомендует брать один длинный шнур. Шнур нужно пропустить через первое отверстие первой подвески и привязать к ней, чтобы он не выскальзывал. Затем его нужно продеть сквозь первое отверстие второй подвески и, пропустив в обратном направлении через среднее отверстие все той же второй подвески, продеть через среднее отверстие первой подвески, после чего продеть в обратном направлении через третье отверстие первой подвески и, продев сквозь третье отверстие второй подвески, завязать свободный конец шнура узлом. Шнур свободно может проскальзывать в отверстия, что облегчает все манипуляции по сравнению с конструкцией, в которой используются три отдельных шнура. Один читатель сообщил нам, что он соединил свои подвески тремя отрезками гибкого шнура и обнаружил, что это также облегчает все манипуляции. Игру можно усложнять, вводя все новые и новые шнуры, но и при трех шнурах она весьма непроста.

Из рис. 183 видно, что описывающая танглоид группа неабелева (то есть некоммутативна). Таблицы для абелевых групп симметричны относительно диагонали, идущей из левого верхнего в правый нижний угол. Иначе говоря, треугольные части таблицы, лежащие по обе стороны этой диагонали, служат зеркальным отражением одна другой.

Если в игру с блужданием по сети линий "основы" и "утка" играют не втроем, а вчетвером, то ее группой будет группа перестановок четырех символов. Эта группа не совпадает с группой, описывающей повороты и отражения квадрата, потому что некоторые перестановки вершин квадрата нельзя получить с помощью одних лишь поворотов и отражений. Преобразования квадрата образуют "подгруппу" группы перестановок четырех символов. Все конечные группы (то есть группы с конечным числом элементов) либо являются группами перестановок, либо входят как подгруппы в какую-нибудь из групп перестановок.

В статье Артина по теории кос^* дается метод приведения любой косы к ее "нормальной" форме. Первая прядь "нормальной" косы полностью выпрямлена, вторая может охватывать первую прядь петлями, третьей пряди разрешается описывать петли вокруг первой и второй прядей и т. д. "Хотя доказано, что всякую косу можно привести к эквивалентной ей нормальной форме,- пишет Артин,- автор на своем собственном опыте убедился, что любая попытка осуществить предсказанное наживой персоне приводит лишь к бурным протестам с ее стороны и оскорбительным выпадам против математики".

^* (Е. Artin, Theory of Braids, Annals of Mathematics, 48, № 1, January 1947, pp. 101-126.)

Три задачи "на расплетание" кос решаются следующим образом:

1. Пропустите подвеску под шнуром С справа налево, а затем под шнурами А и В слева направо.
2. Пропустите подвеску под серединой шнура В слева направо.
3. Пропустите подвеску под всеми шнурами слева направо.

Глава 37. Восемь задач

1. Как разрезать тупоугольный треугольник на остроугольные? Пусть дан тупоугольный треугольник. Можно ли разрезать его на меньшие треугольники так, чтобы все они были остроугольными? (Остроугольным мы называем треугольник, у которого все три угла острые. Прямой угол, разумеется, не является ни тупым, ни острым.) Если этого сделать нельзя, докажите почему. Если можно, то возникает новый вопрос: каково наименьшее число остроугольных треугольников, на которые его можно разрезать?

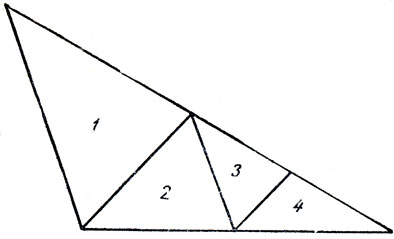
Рис. 187. Можно ли разрезать этот треугольник на остроугольные треугольники меньших размеров?

На рис. 187 показана типичная безуспешная попытка решить задачу. Треугольник разбит на три остроугольных треугольника,но четвертый треугольная тупоугольным, поэтому три предыдущих разрезания ничего не дают.

Эта задача представляет большой интерес, потому что вводит в заблуждение и заставляет делать неверные заключения даже очень сильных математиков. Удовольствие, которое я получил, размышляя над ней, побудило меня поставить другой вопрос. Чему равно наименьшее число остроугольных треугольников, на которые можно разрезать квадрат? В течение нескольких дней я был убежден, что минимальное число равно девяти, но потом вдруг увидел, что его можно понизить до восьми. Интересно, сумеете ли вы найти решение с восемью треугольниками. Может быть, вам даже удастся улучшить мой результат и разрезать квадрат на еще меньшее число остроугольных треугольников. Я не смог доказать, что восемь - это минимум, хотя сильно подозреваю что это так.

2. Чему равен один "лунар"? Герои романа Герберта Уэллса "Первые люди на Луне" обнаружили, что наш естественный спутник населен разумными насекомообразными существами, обитающими в пещерах под лунной поверхностью. Предположим, что эти существа пользуются единицей длины, которую мы назовем "лунаром". Она выбрана так, что площадь лунной поверхности, выраженная в квадратных лунарах, в частности, совпадает с объемом Луны в кубических лунарах. Диаметр Луны составляет 3476 км. Скольким километрам равен один лунар?

3. Игра в гугол. В 1958 году Джон Г. Фокс младший и Л. Джеральд Марни изобрели необычную игру, которую они назвали "гугол". Играют в нее так. Попросите кого-нибудь взять сколько угодно небольших листочков бумаги и написать на них различные положительные числа (по одному числу на каждом листке). Числа могут быть любыми: от самых маленьких дробей до "гугола" - числа, состоящего из 1 и ста нулей,- и даже больше. Листочки ваш партнер раскладывает на столе так, чтобы написанные на них числа были обращены вниз, и вы начинаете по очереди переворачивать их. Дойдя до числа, которое, по вашему мнению, является наибольшим из написанных, вы останавливаетесь. Возвращаться и выбирать числа на уже перевернутых листочках не разрешается. Если вы перевернули все листочки, то выбрать можете только то число, которое стоит на самом последнем листке.

По мнению большинства людей, имеется по крайней мере пять шансов против одного, что вы не сможете указать наибольшее число. На самом деле, если вы будете придерживаться оптимальной стратегии, ваши шансы окажутся немного выше одной трети. Возникает два вопроса. Во-первых, в чем состоит оптимальная стратегия? (Заметим, что она не совпадает со стратегией, стремящейся максимизировать значение выбранного числа.) Во-вторых, если придерживаться оптимальной стратегии, то как подсчитать вероятность выигрыша?

Если имеется только два листа бумаги, то вероятность выигрыша равна ¹/₂ независимо от того, какой листок вы выберете. С увеличением числа листков вероятность выигрыша (предполагается, что вы придерживаетесь оптимальной стратегии) убывает, но кривая быстро выходит на горизонтальную асимптоту и при числе листов, превышающем 10, изменяется очень мало. Вероятность выигрыша никогда не опускается ниже ¹/₃. Многие полагают, что, выбирая очень большие числа, они существенно усложняют задачу, однако, как показывает некоторое размышление, величина чисел не играет никакой роли. Необходимо только, чтобы числа на листах можно было расположить в порядке их возрастания.

Игра в гугол имеет много интересных применений. Вот, например, одно из них. Девушка решает выйти замуж до конца года. Она надеется, что ей удастся встретить десять человек, которые сделают ей предложение (получив отказ, каждый из претендентов на ее руку не проявляет особой настойчивости и от дальнейших попыток добиться согласия своей избранницы отказывается). Какой стратегии следует ей придерживаться, чтобы увеличить свои шансы выбрать самого достойного из женихов? С какой вероятностью она добьется успеха?

Оптимальная стратегия состоит в том, чтобы, отвергнув некоторое число листков бумаги (или предложений), выбрать следующее число, которое превосходит наибольшее из отвергнутых чисел. Требуется найти лишь формулу, которая бы показывала, сколько листков следует отбросить в зависимости от полного числа листков.

4. Марширующие курсанты и беспокойный терьер. Курсанты военного училища построены в каре (квадрат со стороной 15 м) и маршируют с постоянной скоростью (рис. 188). Небольшой терьер, любимец роты, выбегает из середины последней шеренги (из точки А на рис. 188) и устремляется по прямой к середине первой шеренги (к точке В). Достигнув цели, он поворачивает и снова бежит по прямой к середине последней шеренги. К моменту его возвращения в точку А курсанты успевают пройти ровно 15 м. Какое расстояние пробежал терьер, если предположить, что он двигался с постоянной скоростью, и пренебречь потерей времени при повороте?

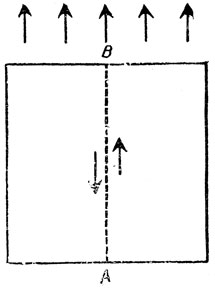
Рис. 188. К задаче о марширующих курсантах и терьере

Решив эту задачу, которая требует лишь знания элементарной алгебры, вы можете испытать свои силы в решении более сложного ее варианта, предложенного уже известным нам изобретателем головоломок Сэмом Лойдом. В этом варианте задачи щенок бегает не вперед и назад через строй марширующих курсантов, а с постоянной скоростью обегает по периметру квадрата (держась все время как можно ближе к своей роте). Как и в предыдущем случае, к моменту его возвращения в точку А курсанты успевают пройти 15 м. Какое расстояние пробегает пес?

5. Пояс Барра. Стивен Барр поведал нам, что у его халата имеется длинный матерчатый пояс, концы которого срезаны под углом 45° (рис. 189). Готовясь к поездке, Барр сложил халат и хотел как можно туже скатать пояс, начав с одного конца, но косо срезанные концы оскорбляли свойственное ему чувство симметрии. Если он подворачивал уголок, чтобы конец пояса был прямым, то необычная толщина конца при скатывании пояса приводила к уродливым выступам и буграм. Он пытался прибегнуть к более хитроумным способам, но безуспешно. Одна из таких неудачных попыток показана на рис. 189: на участке А пояс сложен втрое, а на участке В - всего лишь вдвое.

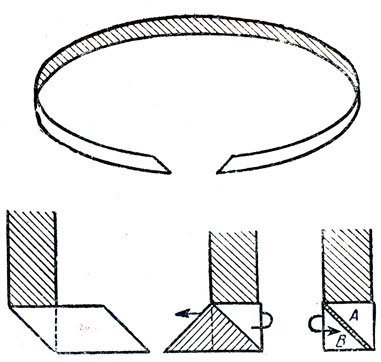
Рис. 189. Пояс Барра и один из неправильных способов его укладки

Все же Барру удалось в конце концов так сложить свой пояс, что каждый конец его был прямым, а весь пояс в сложенном состоянии имел форму прямоугольника и имел всюду одинаковую толщину, после чего его уже нетрудно было скатать в ровный, тугой рулон.

Как Барр сложил свой пояс? При решении задачи можно пользоваться длинной полоской бумаги, концы которой обрезаны под углом 45°.

6. Уайт, Блэк и Браун^*. Профессор математического факультета Мерль Уайт, профессор философии Лесли Блэк и секретарь деканата Джин Браун завтракали за одним столом.

^* (По-английски "уайт" - белый, "блэк" - черный, "брауи" - каштановый (цвет волос).- Прим. перев.)

- Разве не удивительно,- заметила девушка,- что наши фамилии Блэк, Браун и Уайт и что у одного из нас волосы черные, у другого - каштановые, а у третьего - совсем белые?

- Действительно, забавно,- заметила особа с черными волосами.- А вы не обратили внимания, что у одного из нас цвет волос соответствует фамилии?

- Ей богу, вы правы!- воскликнул (или воскликнула) профессор Уайт.

Какого цвета волосы у профессора Блэка, если цвет волос у девушки не каштановый?

7. Самолет и ветер. Самолет летит по прямой из аэропорта А в аэропорт В, а затем обратно из В в А снова по прямой. Он летит с постоянной скоростью, ветер отсутствует. Будет ли время в пути больше, меньше или останется таким же, если полет происходит по тому же маршруту, с той же скоростью, но на обоих отрезках пути дует с одинаковой скоростью ветер? Направление ветра - из А в В:

8. Сколько стоят обитатели зоомагазина? Владелец небольшого зоомагазина приобрел некоторое количество хомяков и вдвое меньшее количество пар длиннохвостых попугаев. За каждого хомяка он заплатил по два доллара, а за каждого попугая - по одному. При продаже он запрашивал за каждого из них цену на 10% больше той, что платил сам.

Распродав всех хомяков и попугаев, кроме семи, владелец магазина обнаружил, что выручка от продажи в точности равна сумме, затраченной им на всю покупку. Следовательно, его потенциальная прибыль равна общей цене оставшихся семи хомяков и попугаев.

Сколько стоит оставшаяся живность?

1. Разрезать тупоугольный треугольник на остроугольные можно всегда. Схема разрезания на семь остроугольных треугольников, применимая к любому тупоугольному треугольнику, показана на рис. 190.

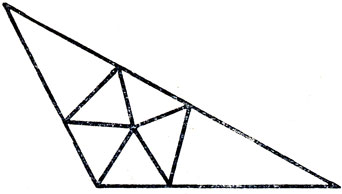
Рис. 190. Тупоугольный треугольник, разрезанный на семь остроугольных треугольников

Нетрудно видеть, что число семь минимально. Тупой угол должен быть разрезан по какой-то прямой. Эта прямая не может доходить до противолежащей стороны, ибо тогда получился бы другой тупоугольный треугольник, который в свою очередь нужно было бы разрезать, вследствие чего схема разрезания большого треугольника не была бы минимальной. Поэтому линия, по которой разрезают тупой угол, должна заканчиваться в некоторой точке внутри треугольника. В этой точке должны сходиться по крайней мере пять линий разреза, в противном случае не все углы при этой вершине были бы острыми. Отсюда получается внутренний пятиугольник из пяти остроугольных треугольников, а общее число остроугольных треугольников становится равным семи.

Возникает вопрос: можно ли произвольный тупоугольный треугольник разрезать на семь остроугольных равнобедренных треугольников? Оказывается, этого сделать нельзя^*. А вот прямоугольный и остроугольный треугольники (каждый из них в отдельности) можно разрезать на девять остроугольных равнобедренных треугольников, а остроугольный равнобедренный треугольник можно разрезать на четыре одинаковых равнобедренных треугольника, подобных исходному.

^* (Доказательство этого см. в American Mathematical Monthly, November 1961, pp. 912-913; June-July 1962, pp. 550-552.)

Квадрат можно разрезать на восемь остроугольных треугольников так, как показано на рис. 191. Если линии разрезов симметричны относительно вертикальной оси квадрата, то точки Р и Р' должны лежать внутри заштрихованной области, граница которой образована дугами четырех полуокружностей. Возможно и асимметричное расположение линий разрезов, при котором точка Р выходит за пределы заштрихованной области, но остается внутри двух больших полукругов.

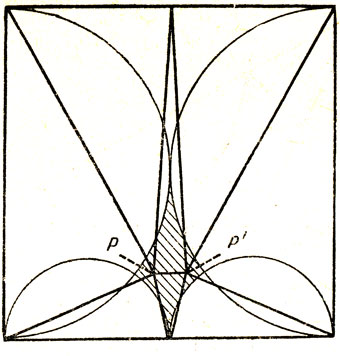
Рис. 191. Квадрат, разрезанный на восемь остроугольных треугольников

Г. С. М. Коксетер обратил внимание на удивительный факт: для любого прямоугольника, как бы мало ни отличались по длине его стороны, отрезок РР' всегда можно переместить в центр квадрата, так что линии разрезов будут симметричны не только относительно вертикальной, но и относительно горизонтальной оси.

Нельзя не упомянуть и два нерешенных вопроса. Квадрат можно разрезать на одиннадцать равнобедренных остроугольных треугольников. Минимально ли это число? Существует ли четырехугольник, который нельзя было бы разрезать на восемь или меньшее число остроугольных треугольников?

На рис. 192 показаны схемы разрезания пентаграммы (правильной пятиконечной звезды) и греческого креста на наименьшее из возможных число остроугольных треугольников.

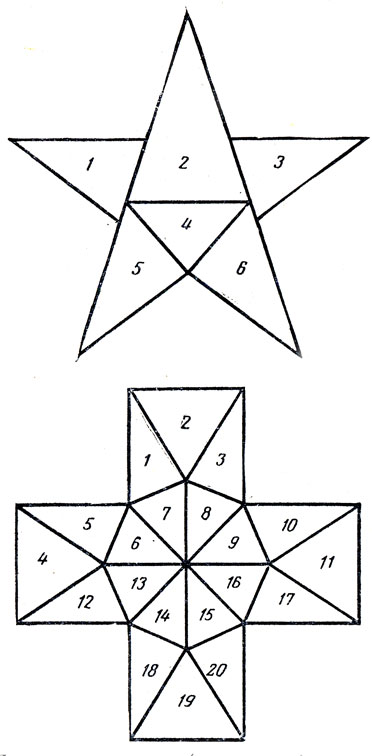
Рис. 192. Пятиугольная звезда (пентаграмма) и греческий крест, разрезанные на минимальное число остроугольных треугольников

2. Объем сферы равен кубу ее радиуса, умноженному на 4π/3. Площадь поверхности сферы равна квадрату ее радиуса, умноженному на 4π. Выразив радиус Луны в лунарах и предположив, что ее поверхность в квадратных лунарах 0 ее объему в кубических лунарах, мы сможем определить длину радиуса, если приравняем оба выражения и решим полученное уравнение относительно радиуса. Число я сокращается и в правой и в левой части, и мы получаем, что радиус Луны равен трем лунарам6льку радиус Луны равен 1738 км, один лунар равен 579 ¹/₃ км.

3. Независимо от того, сколько листков бумаги берут играющие в гугол, вероятность выбрать листок с наибольшим числом никогда не опускается ниже 0,367879 (предполагается, что играющий придерживается оптимальной стратегии). Эта на обратна числу е и служит пределом вероятности выигрыша, когда число листков стремится к бесконечности.

Если для игры взято десять листков (это число особенно удобно), то вероятность выбрать листок с наибольшим числом равна 0,398. Оптимальная стратегия состоит в том, чтобы, перевернув три листка, выбрать наибольшее из значащихся на них чисел, а затем продолжать переворачивать листки до тех пор, пока не встретится еще большее число. При достаточно продолжительной игре такая тактика гарантирует выигрыш в двух случаях из пяти возможных.

Анализ игры в гугол сводится к следующему. Пусть n - число листков бумаги, взятых для игры, p - число листков, перевернутых до того, как было выбрано число, превосходящее любое из чисел, проставленных на этих листках. Перенумеруем листки по порядку от 1 до n. Пусть (k + 1) - номер листка с наибольшим числом. Для того чтобы мы могли выбрать наибольшее число, k должно быть не меньше р (в противном случае, при k <p, наибольшее число будет для нас безвозвратно "утеряно", так как окажется на одном из р первых листков), при этом наибольшее из чисел на листках от 1 до k должно одновременно быть наибольшим из чисел от 1 до р (в противном случае мы бы не смогли дойти до наибольшего из всех чисел, так как остановили бы свой выбор на наибольшем из чисел, значащихся на листках с номерами от 1 до р). Вероятность найти наибольшее число, если оно выписано на (k+1)-м листке, равна p/k, а вероятность того, что наибольшее число действительно стоит на (k + 1)-м листке, равна 1/n. Поскольку наибольшее число может стоять только на одном листке, мы получаем для вероятности "накрытия" этого числа следующую формулу:

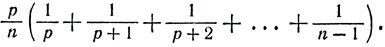
При заданном значении n (числа листков) формула позволяет находить оптимальное значение р (числа листков, которые нужно перевернуть) - то значение р, при котором выписанное выражение достигает максимума. При n, стремящемся к бесконечности, р/n стремится к n/е, поэтому хорошим приближением для р можно считать ближайшее к n/е целое положительное число. Итак, при игре с n листками общая стратегия заключается в том, чтобы переворачивать листки до тех пор, пока их число не превысит n/е, а затем выбрать первое же число, большее максимального, из чисел, записанных на перевернутых n/е листках.

Разумеется, приведенное выше рассуждение исходит из предположения о том, что играющему не известны наибольшее и наименьшее из чисел, выписанных на листках, и поэтому, увидев очередное число, он не может судить о том, насколько близко оно к верхней или нижней границе того отрезка числовой оси, которой принадлежит выбранное число. Если играющий располагает такими сведениями, то все рассуждение становится неприменимым. Например, если вместо листков бумаги при игре в гугол взять десять долларовых купюр с их банковскими номерами, то, вытащив доллар, номер которого начинается с девятки,, вам лучше всего объявить этот номер наибольшим. По аналогичным причинам игра в гугол, если говорить строго, неприменима и к задаче о девушке, жаждущей выйти замуж, ибо, как отметили многие читатели, девушка, по-видимому, великолепно осведомлена о достоинствах своих поклонников и подходит к ним с определенными мерками. Если первый же, кто делает ей предложение, очень близок к ее идеалу, то, как написал нам один из читателей, "она будет просто дурой, если не примет предложения".

Задача о максимизации значения выбранного объекта (а не вероятности выбора объекта с наибольшим значением), насколько известно, была впервые поставлена знаменитым математиком Артуром Кэли в 1875 году.

4. Примем за единицу длины ширину (или равную ей глубину) строя курсантов, а за единицу времени - то время, которое требуется им, чтобы пройти единицу длины. В принятых единицах скорость передвижения строя также будет единичной. Пусть х - полное расстояние, пройденное терьером (его скорость будет выражаться той же величиной х). Когда пес бежит к первой шеренге, его скорость относительно курсантов равна х-1. При возвращении в последнюю шеренгу скорость терьера составляет х + 1. Каждый раз он пробегает (относительно строя) расстояние 1 и на путешествия в оба конца затрачивает единицу времени. Это позволяет нам составить уравнение

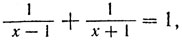
которое можно переписать в виде квадратного уравнения х²-2х-1 = 0. Положительный корень этого уравнения равен 1 + √2. Умножив его на 15, получаем окончательный ответ: 36,15... м. Иначе говоря, терьер пробегает расстояние, равное длине стороны квадрата, в форме которого выстроены курсанты, плюс расстояние, равное длине диагонали того же квадрата.

Аналогичным образом получается приближенный ответ и для лойдовского варианта задачи, когда собачка бегает вокруг марширующего строя.

Пусть, как и прежде, ширина строя равна единице и единице равно время, за которое курсанты проходят 15 м. Тогда и скорость их также равна 1. Пусть х - расстояние, пройденное собакой (и скорость собаки). Скорость собаки относительно строя равна х - 1, когда собака бежит от последней шеренги к первой, √(х²-1) когда собака бежит поперек строя, и х + 1, когда собака возвращается в последнюю шеренгу. Так как собака обегает строй за единицу времени, можно составить уравнение

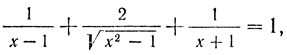
которое можно переписать в виде уравнения четвертой степени: х⁴ - 4х³ - 2х² + 4х + 5 = 0. Только один положительный корень х = 4,18112... не является посторонним. Умножив его на 15, получим ответ: 62,7168... м.

Исходную форму полученного выше уравнения можно привести к виду

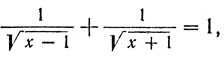
очень похожему на уравнение, возникающее в первичном варианте задачи. Чтобы выполнить преобразование, нужно лишь извлечь квадратные корни из правой и левой частей исходного уравнения.

Возможны многочисленные варианты этой задачи? для строя, марширующего в направлении, параллельном диагонали квадрата; для строев, имеющих форму правильных многоугольников с числом сторон, превышающим 4; для "построений по кругу, вращающихся строев и т. п.

Задача о терьере - это лишь иная формулировка задачи об истребителе-перехватчике, совершающем разведывательный полет по сторонам квадрата, в центре которого находится движущееся судно. Она легко решается с помощью векторных диаграмм на "планшете", на который в военно-морском флоте принято наносить обстановку.

5. Простейший способ укладки пояса Барра, при котором концы пояса оказываются прямыми, а сам он принимает вид прямоугольника, имеющего всюду одинаковую толщину, показан на рис. 193. Это позволяет скатать пояс в аккуратный валик без каких-либо уродливых выступов (что хоть в какой-то мере вознаграждает нас за длительную возню с его укладкой). Предложенный способ пригоден при любой длине пояса и всегда приводит к желаемому результату независимо от того, под каким углом обрезаны углы пояса.

Рис. 193. Как Барр сложил свой пояс

6. Предположение о том, что "девушка" - это Джин Браун, секретарь факультета, быстро приводит к противоречию. На первую реплику секретаря отвечает особа с черными волосами, поэтому волосы Браун не могут быть черными. Но они не могут быть и каштановыми, ибо тогда их цвет соответствовал бы фамилии. Поэтому волосы Браун могут быть только белыми. Такое заключение означает, что профессор Блэк имеет каштановые волосы, а профессор Уайт - черные. Но замечание особы с черными волосами вызывает восклицание у профессора Уайта, в силу чего они не могут быть одним и тем же лицом.

Таким образом, нам не остается ничего другого, как предположить, что Джин Браун мужчина. Волосы профессора Уайта (или Уайт) не могут быть белыми (ибо тогда их цвет соответствовал бы его или ее фамилии), не могут они быть и черными, поскольку профессор Уайт ответил особе с черными волосами. Следовательно, они должны быть каштановыми. Если у девушки не каштановые волосы, то профессор Уайт не может быть девушкой. Браун мужчина, поэтому девушкой должен быть профессор Блэк. Так как ее волосы не могут быть ни черными, ни каштановыми, она должна быть платиновой блондинкой.

7. Поскольку при полете из А в В дует попутный, а при полете из В в А - встречный ветер, многие поддаются искушению и думают, что опережение графика в первом случае и запоздание во втором компенсируют друг друга, так что полное время в полете остается таким же, как и при отсутствии ветра. Такое заключение неверно, ибо время полета с попутным ветром меньше, чем время полета против встречного ветра, в силу чего в итоге самолет запаздывает. Полное время полета при постоянном по величине и направлению ветре, независимо от этой величины и направления, всегда больше, чем в безветренную погоду.

8. Пусть х - число первоначально купленных хомяков (и равное ему число купленных попугаев), y - число хомяков среди семи оставшихся непроданными обитателей зоомагазина. Тогда число непроданных попугаев равно 7-y. Число проданных хомяков (по цене 2,20 доллара за штуку -2 доллара "себестоимость" + 10% надбавки) равно х - y, а число проданных попугаев (по 1,10 доллара за каждого) равно х - 7 + y.

Вырученная хозяином сумма составляет 2х долларов за хомяков и х долларов за попугаев, то есть всего 3х долларов. От продажи хомяков хозяин получил 2,2(х-y) долларов, а от продажи попугаев - 1,1(х - 7 + y) долларов, то есть всего 3,3x - 1,1y - 7,7 доллара.

Приравняв оба полученных выражения для выручки, мы после упрощений получим следующее диофантово уравнение с двумя целочисленными неизвестными:

Поскольку х и y - целые положительные числа и y не может превышать 7, проще всего подставить вместо y восемь возможных значений (в том числе и нулевое) и посмотреть, при каком из них х также принимает целое значение. Таких значений только два: 5 и 2. Каждое из них можно было бы считать решением задачи, если бы не одно обстоятельство: попугаев покупают парами. Это дополнительное условие исключает y = 2, так как при этом х (число проданных попугаев) был бы равен нечетному числу 33. Следовательно, y = 5.

Теперь уже ничто не мешает нам восстановить полную картину. Владелец зоомагазина приобрел 44 хомяка и 22 пары длиннохвостых попугаев, уплатив за всю покупку 132 доллара. Он продал 39 хомяков и 21 пару попугаев за 132 доллара. Оставшиеся пять хомяков стоят (с учетом надбавки) 11 долларов, а два попугая - 2,20 доллара, то есть всего 13,20 доллара. Эта сумма - ответ задачи - и определяет потенциальную прибыль хозяина.