Глава 35. Двоичная система

В настоящее время во всем цивилизованном мире принята десятичная система записи чисел, основанная на использовании последовательных степеней числа 10. Самая правая цифра любого числа указывает, сколько в нем содержится единиц, то есть 10⁰. Вторая от конца цифра указывает количество десятков, то есть 10¹; третья - число сотен, то есть 10², и т. д. Например, 777 в десятичной системе означает сумму (7*10⁰) + (7*10¹) + (7*10²). Столь широкое распространение числа 10 в качестве основания системы счисления объясняется тем, что у нас на руках десять пальцев. Не случайно английское слово "digit" имеет два значения: "палец" и "цифра". Если на Марсе обитают человекоподобные существа с двенадцатью пальцами, то можно с уверенностью сказать, что марсианская арифметика использует двенадцатеричную систему счисления с основанием 12.

Простейшей из всех числовых позиционных систем следует считать двоичную систему счисления с основанием 2. Двоичной системой пользовались при счете некоторые первобытные племена, она была известна еще древнекитайским математикам, но по-настоящему развил и построил двоичную систему великий немецкий математик Лейбниц, видевший в ней олицетворение глубокой метафизической истины. Нуль для Лейбница был символом небытия, пустоты, единица - символом бытия или материи. Он полагал, что и нуль, и единица в равной степени необходимы создателю, ибо Вселенная, состоящая из одной лишь чистой материи, была бы неотличима от пустой, ничем не возмущаемой Вселенной, которую символизирует 0. По Лейбницу, все в мире сотворено из двух противоположных начал - бытия и небытия, так же как любое число в двоичной системе представлено одними лишь нулями и единицами.

Со времен Лейбница и вплоть до недавнего времени двоичную систему считали не более чем занятным курьезом, лишенным какой бы то ни было практической ценности. Но вот появились вычислительные машины. Многие их детали работают по принципу "да - нет": ток либо течет по проводнику, либо не течет; переключатель находится либо в положении "включено", либо в положении "выключено"; полюс магнита может быть либо северным, либо южным, ячейка памяти находится только в одном из двух состояний. Это и позволяет конструировать вычислительные машины, способные с огромной быстротой и точностью перерабатывать входные данные, закодированные в двоичной системе. "Увы!- пишет известный голландский математик Т. Данциг в своей книге "Число - язык науки",- то, что некогда возвышалось как монумент монотеизму, очутилось во чреве робота".

Во многих математических играх также используется двоичная система. Назовем хотя бы игру в ним (см. главу 14), такие механические головоломки, как Ханойская башня и кардановы кольца, и бесчисленные фокусы с перфокартами. В этой главе мы расскажем лишь об известном наборе специальных карт, позволяющих "читать мысли", и тесно связанном с ним наборе перфокарт, пользуясь которыми, вы сможете показать несколько замечательных "двоичных" фокусов,

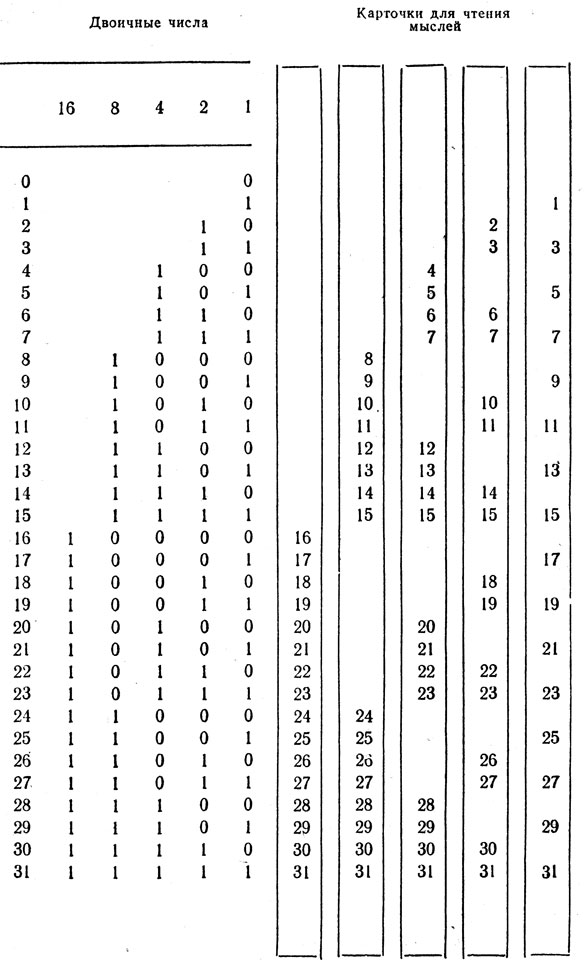
Принцип карт, позволяющих "читать мысли", ясен из приведенной выше таблицы. В ее левой части выписаны двоичные числа от 0 до 31. Каждая цифра двоичного числа - это коэффициент при некоторой степени двойки. Самая правая цифра означает коэффициент при 2⁰, или 1. Затем справа налево идут коэффициенты при 2¹ (или 2), 2², 2³ и т. д. Степени двойки указаны над каждым столбцом. Чтобы перевести двоичное число в десятичное, нужно просто сложить те степени двойки, которые встречаются с единичным коэффициентом. Так, двоичное число 10101 означает 16 + 4 + 1, или 21. Чтобы десятичное число 21 перевести в двоичную систему, нужно проделать обратную процедуру. Поделив 21 на 2, мы получим 10 и 1 в остатке. Этот остаток и будет самой правой цифрой двоичного числа. Поделив 10 на 2, мы не получим остатка, поэтому на втором месте справа следует написать 0. Затем нужно поделить 5 на 2 и продолжать в том же духе до тех пор, пока не получим двоичное число 10101. Самая левая ("старшая") цифра числа получается так: 2 входит в 1 нуль раз, а остаток равен 1.

Таблицу двоичных чисел легко превратить в набор карт для угадывания мыслей: нужно заменить каждую единичку тем десятичным числом, в двоичной записи которого она встречается. Результат такой подстановки показан в правой части таблицы. Каждый столбец чисел выписывается на отдельной карточке. Дайте кому-нибудь все пять карт, попросите задумать любое из чисел от 0 до 31 и вернуть вам те карточки, на которых встречается выбранное число. Получив карточки, вы сразу же можете назвать задуманное число: чтобы узнать его, нужно лишь сложить самые верхние числа на возвращенных вам карточках.

Как получается этот фокус? Каждое задуманное число задает особую, неповторяющуюся комбинацию карт. Эта комбинация эквивалентна двоичной записи чисел. Складывая верхние числа, стоящие на возвращенных карточках, вы просто находите сумму тех степеней двойки, которые входят в двоичное разложение задуманного числа с коэффициентом 1. Чтобы еще сильнее запутать зрителей, можно воспользоваться разноцветными карточками. Вы уходите в противоположный конец комнаты и просите зрителя положить карточки с задуманным им числом в один карман, а остальные карточки - в другой. Разумеется, вы должны видеть отобранные карточки и помнить, какая степень двойки соответствует каждому цвету. Тот же фокус можно показывать и по-другому. Разложите пять карточек (на этот раз их не нужно раскрашивать) в ряд на столе. Встав в другом конце комнаты, попросите кого-нибудь перевернуть карточки с задуманным им числом. Так как карточки расположены в порядке возрастания верхних чисел, вам остается лишь сложить верхние числа на перевернутых карточках и получить ответ.

Не менее интересные фокусы можно показать с помощью набора перфокарт, изображенного на рис. 179. Они также основаны на использовании двоичной системы. Перфокарты можно изготовить из обычных карточек, используемых в библиотечных каталогах, картотеках и т. п. Отверстия должны быть чуть больше диаметра карандаша. Удобно сначала прорезать пять отверстий в одной карточке, а затем использовать ее как шаблон для того, чтобы наметить отверстия на других карточках. Если у вас нет дырокола, прорезание отверстий ножницами можно ускорить, если брать по три карточки и прорезать в них отверстия одновременно. Срезанный угол позволяет следить за тем, чтобы перфокарты не переворачивались. Проделав в каждой карточке по пять отверстий, прорежьте промежуток, отделяющий некоторые отверстия от края, так, как показано на рис. 179. Отверстия, доходящие до края перфокарт, соответствуют цифре 1, остальные отверстия соответствуют цифре 0. Таким образом, каждой перфокарте можно сопоставить некоторое двоичное число от 0 до 31, но карточки на рис. 179 нарисованы в беспорядке. С помощью этих перфокарт можно показать три необычных фокуса. И хотя изготовить карты довольно хлопотно, все члены вашей семьи с удовольствием будут забавляться ими.

Рис. 179. Набор перфокарт, позволяющий прочесть новогоднее поздравление, отгадать задуманное число и решить некоторые логические задачи

Первый фокус заключается в быстрой сортировке перфокарт: нужно расположить их так, чтобы соответствующие перфорации числа последовательно возрастали от 0 до 31.

Перетасуйте перфокарты, как игральные, и сложите их колодой. Продев карандаш в отверстие Е, немного приподнимите его. Половина карт окажется надетой на карандаш, а половина останется в колоде. Встряхните карандаш, чтобы те карты, которые должны остаться в колоде, не оказались вынутыми, и, подняв карандаш, разделите колоду на две части. Снимите с карандаша надетые на него карты и положите их поверх остальной колоды. Затем по очереди проделайте эту же процедуру, продевая карандаш в каждое из отверстий по порядку справа налево. Дойдя до пятого отверстия, вы с удивлением обнаружите, что двоичные числа, соответствующие перфорации карт, расположились по порядку от 0 до 31, а перелистав карточки, прочтете новогоднее поздравление.

Рис. 180. Дополнительный ряд отверстий у нижнего края этих карточек позволяет безошибочно сортировать их

Во втором фокусе перфокарты играют роль вычислительного устройства, позволяющего отгадывать числа, выписанные на карточках для "чтения мыслей". Продев карандаш в отверстие Е, спросим, встречается ли задуманное число на карточке, самое верхнее число которой равно 1. При утвердительном ответе нужно поднять карандаш и отбросить все карты, оказавшиеся надетыми на него. При отрицательном - отбросить карты, оставшиеся в колоде. И в том и в другом случае у вас останется 16 карт. Спросите у вашего зрителя, находится ли задуманное им число на карточке с верхним числом 2, и повторите только что проделанные операции, продев карандаш в отверстие D. После того как ваш карандаш побывает во всех отверстиях (а вы спросите, находится ли задуманное число на соответствующей карточке, и в зависимости от ответа оставите или отбросите надетые на карандаш перфокарты), у вас останется одна-единственная перфокарта. Пробитые на ней отверстия будут образовывать двоичную запись задуманного зрителем числа. Если хотите, на каждой карточке можно заранее напечатать соответствующее десятичное число. Тогда вам не надо будет каждый раз переводить числа из двоичной системы в десятичную.

В третьем фокусе перфокарты служат своего рода логической машиной, идея которой была впервые предложена английским экономистом и логиком Уильямом С. Джевонсом. В "логическом абаке", как назвал свое устройство Джевонс, используются деревянные дощечки с воткнутыми в них стальными булавками, за эти булавки дощечки можно вынимать из специальной рамки. Однако манипулировать с перфокартами ничуть не хуже, а изготовить их намного проще. Джевонс изобрел также и сложное механическое устройство, названное им "логическим пианино", но и тут перфокарты с успехом позволяют исполнять все то, что можно "исполнить" на логическом пианино. На самом деле перфокарты обладают даже более широкими возможностями, поскольку пианино позволяет учесть лишь четыре высказывания, а перфокарты - пять.

Пяти высказываниям А, В, С, D и Е соответствуют пять отверстий, каждое из которых в свою очередь означает двоичную цифру. Единица (или отверстие, прорезанное до края перфокарты) отвечает истинному высказыванию, нуль - ложному. Горизонтальная черточка над буквой означает, что данное высказывание ложно, в противном случае высказывание считается истинным. Каждая карточка представляет собой неповторяющуюся комбинацию истинных и ложных высказываний, а так как 32 карточки исчерпывают все возможные комбинации, их набор можно рассматривать как эквивалент так называемой таблицы истинности для сложных суждений, составленных из пяти элементарных суждений А, В, С, D и Е. Действие перфокарт лучше всего объяснить на примере, показывающем, как с их помощью можно решать задачи двузначной логики.

Следующая головоломка заимствована нами из одной недавно вышедшей книги.

"Если Сара не должна выполнить поручение, его выполняет Ванда. Утверждения "Сара должна" и "Камилла не может" не могут быть истинными одновременно. Если Ванда выполняет поручение, то Сара должна, а Камилла может выполнить его. Итак, Камилла всегда может выполнить поручение. Правильно ли такое заключение?"

Чтобы решить эту задачу, возьмем колоду наших перфокарт (расположение карт в колоде роли не играет). Поскольку в условии задачи фигурируют лишь три высказывания, будем рассматривать только три отверстия А, В и С.

Условие задачи состоит из трех посылок. Первая - "Если Сара не должна выполнить поручение, его выполняет Ванда" - сообщает нам, что комбинация 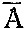и 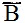недопустима и мы должны изъять из колоды все карточки, на которых она встречается. Сделать это можно так. Введем карандаш в отверстие А и приподнимем его. Все карточки, оказавшиеся на карандаше, соответствуют высказыванию 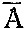. Снимем их с карандаша, введем его в отверстие 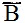и поднимем еще раз. На этот раз на карандаш будут надеты все карточки с запрещенной комбинацие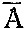й и 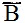, и мы их отбросим. Все остальные карточки сложим в одну колоду (порядок карточек и на этот раз роли не играет). Теперь мы готовы ко второй посылке: утверждения "Сара должна" и "Камилла не может" не могут быть истинными одновременно. Иначе говоря, комбинация А 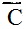недопустима. Просунув карандаш в отверстие А и подняв его, мы извлечем из колоды все карты с 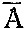, но это не те карты, которые нам нужны. Поэтому мы временно отложим их в сторону и обратимся к оставшимся картам, на которых значится А. Введя карандаш в отверстие С, извлечем карты с 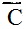. Именно на этих картах фигурирует недопустимая в силу второго условия комбинация А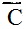, и их заведомо можно отбросить. Оставшиеся и временно отложенные карты объединяем в одну колоду.

Из последней посылки мы знаем, что если Ванда выполняет поручение, то его должна выполнить Сара и может выполнить Камилла. Немного подумав, можно понять, что это условие исключает две комбинации: 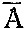В и В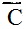. Введем карандаш в отверстие А, поднимем и возьмем нанизанные на карандаш карты. Если теперь ввести карандаш в отверстие В этих карт, то, подняв карандаш, мы не обнаружим на нем ни одной карты. Это означает, что две предыдущие посылки уже сделали комбинацию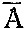 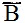невозможной. Поскольку все эти карты содержат недопустимую комбинацию АВ, их можно отбросить. Нам нужно еще исключить из остальных карт те, которые содержат комбинацию В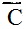. Введем карандаш в отверстие В и, вытащив карты с 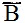, отложим их временно в сторону. Продев карандаш в отверстие С оставшихся в колоде карт, мы не "выудим" из нее ни одной карты. Следовательно, недопустимая комбинация В 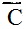уже была отброшена раньше.

Итак, у нас остается лишь восемь карт, на каждой из которых выписана комбинация А, В и С, совместимая со всеми тремя условиями задачи. При данных посылках этим комбинациям в таблице истинности отвечает значение "истина". Просмотрев все восемь карт, мы убедимся в том, что С на всех картах имеет значение "истина". Это и означает, что заключение о том, будто Камилла всегда может выполнить поручение, верно. Из тех же посылок можно вывести и другие заключения. Например, можно утверждать, что Сара должна выполнить поручение. Но интересный вопрос, выполнит его Ванда или нет, остается неразрешимой ("двоичной") загадкой, во всяком случае при тех сведениях, которыми мы располагаем.

Для тех, кто хотел бы воспользоваться перфокартами для решения других задач, приведем одну несложную задачку. В доме живут: Абнер, его жена Берил и трое их детей - Клео, Дейл и Эллсуорт. Зима. Восемь часов вечера.

1. Если Абнер смотрит телевизор, то и жена его, также смотрит телевизор.
2. Либо Дейл, либо Эллсуорт, либо оба смотрят телевизор.
3. Либо Верил, либо Клео, но не обе смотрят телевизор.
4. Дейл и Клео либо оба смотрят, либо оба не смотрят телевизор.
5. Если Эллсуорт смотрит телевизор, то Абнер и Дейл также смотрят телевизор.

Кто смотрит и кто не смотрит телевизор?

Профессор Априле прислал две фотографии, изображенные на рис. 180. Дополнительный ряд отверстий и прорезей у нижнего края каждой карточки позволяет быстро и безошибочно сортировать карты. Булавки, воткнутые в отверстия нижнего ряда, удерживают карты, остающиеся после изъятия части колоды с помощью булавок, воткнутых в отверстия верхнего ряда.

Логическая задача с помощью перфокарт решается так. Пусть А, В, С, D и Е означают: Абнер, Берил, Клео, Дейл и Эллсуорт. Каждое утверждение считается истинным, если соответствующее лицо смотрит телевизор, в противном случае оно ложно. Услсизие 1 позволяет отбросить все карты с комбинацией А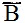; условие 2 - карты с комбинацией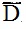 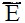; условие 3 исключает комбинации ВС и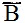 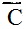; условие 4 исключает комбинации 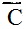D и C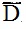; условие 5 исключает комбинации 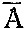Е и D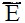. Остается единственная карта с комбинацией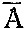 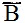CD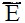. Отсюда мы заключаем, что Клео и Дейл смотрят телепередачу, а остальные члены семьи не смотрят ее.