Глава 6. "Икосаэдрическая игра" и "Ханойская башня" [1971 Гарднер М. - Математические головоломки и развлечения]

Вряд ли что-нибудь может произвести большее впечатление на математика, чем открытие связи между двумя на первый взгляд никак не связанными между собой математическими структурами. Именно такое открытие сделал недавно Д. У. Кроув. Он обнаружил связь между двумя популярными головоломками прошлого века - "Икосаэдрической игрой" и "Ханойской башней". Сначала мы расскажем о каждой головоломке в Отдельности, а затем покажем ту неожиданную связь, которая существует между ними.

Игру с икосаэдром придумал в пятидесятых годах прошлого века знаменитый ирландский математик Уильям Р. Гамильтон. На примере этой игры он хотел продемонстрировать некоторые не совсем обычные свойства разработанного им исчисления, во многом схожего с принадлежащей тому же автору теорией кватернионов (предшественницей современного векторного анализа). Исчисление позволяло решать ряд сложных задач об обходе ребер пяти Платоновых тел, и в частности икосаэдра и додекаэдра. Гамильтон назвал свое исчисление икосаэдрическим, хотя в действительности в придуманной им игре приходится совершать обход ребер додекаэдра. В 1859 году Гамильтон продал игру за 25 долларов одному лондонскому дельцу. Позднее она в различных видах появлялась в Англии и других европейских странах. Биограф Гамильтона сообщает, что эти 25 долларов были единственными деньгами, которые получил известный математик за свои открытия и научные труды.

Гамильтон придумал много игр и головоломок, связанных с додекаэдром, но самой интересной из них была следующая. Начав с любой вершины додекаэдра (каждой его вершине Гамильтон дал название какого-нибудь крупного города), нужно было совершить "кругосветное путешествие" - обойти ровно один раз все ребра правильного многогранника и вернуться в исходную вершину. Иначе говоря, путь должен иметь вид замкнутой ломаной, составленной из всех ребер додекаэдра. Каждое ребро разрешается проходить только один раз. Начало и конец пути должны находиться в одной и той же вершине додекаэдра.

Представьте себе, что поверхность додекаэдра сделана из резины. Проткнув одну из его граней, растянем додекаэдр так, чтобы он целиком распластался на плоскости. Его ребра расположатся в виде сети, показанной на рис. 23. Топологически эта сеть эквивалентна сети, образуемой ребрами "настоящего", несплющенного додекаэдра, но, разумеется, с плоской сетью обращаться намного удобнее, чем с объемной. Совершая "кругосветное путешествие" по этой сети ("карте додекаэдра"), удобно отмечать каждую вершину, в которой вы побывали, фишкой.

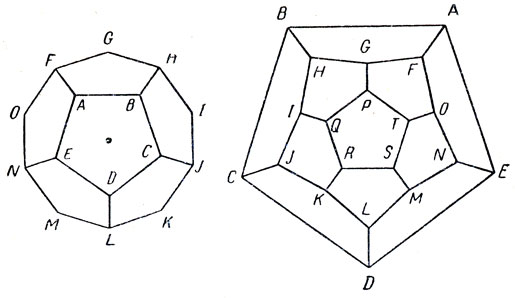
Рис. 23. Додекаэдр (слева) проколотый (место прокола указано точкой) и растянутый на плоскости (справа). Размеры отдельных звеньев сети прямых на плоскости не совпадают с длиной ребер додекаэдра, но топологически сеть прямых на плоскости и сеть, образованная ребрами додекаэдра, эквивалентны

Если все вершины додекаэдра эквивалентны, то существуют только два различных гамильтоновых пути, и любой из них является зеркальным отражением другого. Если же мы введем для каждой вершины особое обозначение и будем считать различными пути, проходящие через все 20 вершин в различном порядке, то таких путей окажется 30 (путь, проходимый в обратном направлении, мы не отличаем от пути, проходимого в прямом направлении). Гамильтоновы пути точно так же можно построить на четырех других Платоновых телах и на многих, хотя и не на всех, полуправильных многогранниках.

Известную игру "Ханойская башня" придумал французский математик Эдуард Люка. В 1883 году ее продавали как забавную игрушку. Первоначально она называлась "Профессор Клаус" ("Claus") из "Коллеж Ли-Су-Стьян" ("Li-Sou-Stian"), но вскоре обнаружилось, что таинственный профессор из несуществующего коллежа - не более чем анаграмма фамилии изобретателя игры - профессора Люка ("Lucas") из коллежа Сен-Луи ("Saint Louis"). Вид игрушки показан на рис. 24. Задача состоит в том, чтобы перенести пирамиду из восьми колец за наименьшее число ходов. За один раз разрешается переносить только одно кольцо, причем нельзя класть большее кольцо на меньшее.

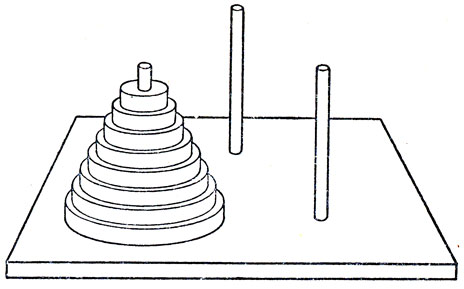
Рис. 24. Ханойская башня

Нетрудно доказать, что решение существует независимо от того, сколько колец в пирамиде, и что минимальное число необходимых перекладываний выражается формулой 2ⁿ-1 (где n - число колец). Таким образом, три диска можно перенести с помощью семи перекладываний; для четырех дисков понадобится шестнадцать перекладываний, для пяти - 31 и т. д. Для восьми колец, изображенных на рис. 24, потребуется 255 перекладываний. В первоначальном описании игрушка называется упрощенным вариантом мифической "Пирамиды браминов" в храме индийского города Бенареса. Как гласит предание, эта пирамида состоит из 64 золотых колец, которые и по сей день перекладывают жрецы храма. Как только им удастся справиться со своей задачей, храм рассыплется в пыль, грянет гром и мир исчезнет. О конце мира еще, пожалуй, можно спорить, но то, что храм за это время обратится в пыль, несомненно. Формула 2⁶⁴-1 дает двадцатизначное число 18446 744 073 703 551615. Даже если бы жрецы работали не покладая рук, днем и ночью, перенося каждую секунду по одному кольцу, чтобы закончить работу, им понадобились бы многие миллионы тысячелетий.

(Получившееся число не является простым, но если число колец увеличить до 89, 107 или 127, то в каждом случае нужное число перемещений будет простым. Эти числа называются числами Мерсенна: простые числа, которые можно представить в виде 2ⁿ-1. Сам Люка был первым, кто установил, что число 2¹²⁷-1 простое. Это огромное 39-значное число было самым большим из всех известных вплоть до 1952 года простых чисел. В 1952 году с помощью большой электронно-вычислительной машины было найдено пять новых чисел Мерсенна. Самое большое из них имеет вид 2²²⁸¹-1. Существует много аргументов в пользу того, что число 2⁸¹⁹¹-1 также простое, но пока это не доказано.)

Головоломку "Ханойская башня" легко сделать из восьми картонных квадратиков постепенно увеличивающегося размера (с тем же успехом можно взять игральные карты от туза до восьмерки), которые нужно перекладывать между тремя отметками на листе бумаги, Если эти отметки образуют треугольник, то задача решается для любого числа колец следующим простым способом. Начнем с самого маленького квадрата и переложим его на любую отметку. В дальнейшем этот квадратик нужно перемещать в том же направлении, что и при первом перекладывании. Затем произведем единственно возможное перемещение оставшихся квадратов, после чего снова переложим самый маленький квадрат и т. д. (Интересно заметить, что, перенумеровав "кольца" по порядку, мы добьемся неожиданного эффекта: четные квадраты будут перемещаться из одной вершины треугольника в другую в одном направлении, а нечетные - в противоположном направлении.)

Что же общего у "Ханойской башни" с игрой, придуманной Гамильтоном? Чтобы понять, как эти две знаменитые головоломки связаны между собой, рассмотрим сначала пирамиду из трех колец, на которых по порядку сверху вниз написаны буквы A, В и С. Следуя описанному выше алгоритму решения задачи, кольца нужно перемещать в следующей последовательности: АВАСАВА.

Обозначим теперь через A, В и С три оси координат, выбранные в направлениях, параллельных осям правильного шестигранника - куба (на рис. 25 - слева). Если, обходя ребра куба, мы будем двигаться по направлениям этих осей в последовательности АВАСАВА, то наш маршрут окажется одним из гамильтоновых путей! Кроув заметил, что этот результат допускает обобщение: порядок перекладывания дисков при игре ""Ханойскую башню" в точности совпадает с порядком, котором мы проходим направления координатных осей при следовании по гамильтонову пути на n-мерном кубе.

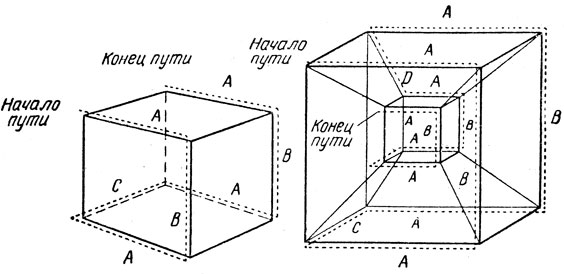
Рис. 25. Путь Гамильтона, приходящий по ребрам куба (слева). Оси координат выбраны параллельно ребрам куба и обозначены буквами А, В и С. Путь последовательно идет по направлениям осей АВАСАВА. Справа показан путь Гамильтона, проходящий по ребрам четырехмерного куба, спроектированного в трехмерное пространство. Оси четырех координат гиперкуба обозначены буквами А, В, С и D. Путь последовательно идет по направлениям осей ABACABADABACABA. В этом же порядке нужно перекладывать четыре диска в 'Ханойской башне'

Поясним сказанное на еще одном примере. Хотя мы и не можем изготовить модель четырехмерного куба (называемого также гиперкубом или тессерактом), тем не менее ребра четырехмерного куба можно спроецировать на трехмерную модель, изображенную на рис. 25. Сеть ребер этой модели топологически эквивалентна сети ребер гиперкуба. Обозначим оси координат буквами. А, В, С и D. Координата D означает расстояние, проходимое по ребрам гиперкуба. Тогда порядок перекладывания для пирамиды из четырех колец будет таким: ABACABADABACABA. Следуя по ребрам гиперкуба в направлениях, указанных этой последовательностью, мы пройдем гамильтонов путь. Аналогичные рассуждения показывают, что перекладывание пяти колец соответствует пути Гамильтона, проложенному по ребрам пятимерного гиперкуба, перекладывание шести колец - гамильтонову пути, проходящему по ребрам шестимерного гиперкуба, и т. д.

Доказательство того, что n колец можно перенести с одного колышка на другой в (2ⁿ-1) приемов, довольно простое и может послужить хорошим упражнением на применение метода полной математической индукции^*. Задача легко обобщается на любое число колышков.

Сходство, или, если воспользоваться научным термином, изоморфизм, решений задач о Ханойской башне и пути Гамильтона на кубе и гиперкубе перестает быть столь удивительным, когда обнаруживается, что и в том и в другом случаях последовательности ходов представляют собой набор чисел, хорошо знакомый каждому, кому доводилось работать на вычислительных машинах с двоичным представлением чисел.

Рис. 26. Таблица двоичных чисел

Выпишем числа от 1 до 8 и обозначим столбцы буквами F, В, С и D так, как показано на рис. 26. Рядом с каждой строкой напишем букву, которая указывает, где в этой строке должна стоять самая правая единица. Прочитав эти буквы сверху вниз, мы получим искомую последовательность.

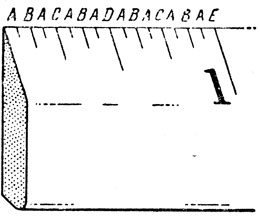
Рис. 27. Двоичные деления дюйма

Таблица эта часто используется в математических головоломках. В качестве примеров можно привести доску с отгадыванием задуманного и старинную головоломку, известную под названием "Китайские кольца". Но самый известный пример - это двоичное разбиение дюймового обрезка обычной линейки (рис. 27). Нетрудно понять, откуда возникает последовательность - она образуется при делении дюймового отрезка на две, четыре, восемь и шестнадцать частей.