Глава 4. Крестики и нолики, или тик-так-тоу

(Тик-так-тоу (англ.) - название игры в крестики и нолики, происходящее от слов детской считалочки.- Прим. перев.)

Кто из нас в детстве не играл в крестики и нолики! Об этом древнем состязании на сообразительность писал еще Уордсворт:

На глади грифельной доски, 
Расчерченной в квадраты, 
Ведем сраженье я и ты, 
Бывалые солдаты. 

Кресты с нулями испестрят 
Все поле битвы густо, 
Но строй их - не могильный ряд 
И не наводит грусти. 

Не нужно нам владеть клинком, 
Не ищем славы громкой. 
Тот побеждает, кто знаком 
С искусством мыслить тонким. 

Не можем мы лишь одного: 
Назвать то состязанье, 
Хоть просты правила его, 
Длинно его названье.

На первый взгляд кажется непонятным, что может так увлекать в этой детской забаве. Правда, даже в самом простом варианте игры число возможных комбинаций чрезвычайно велико (если ограничиться лишь пятью первыми ходами, то и тогда наберется 9×8×7×6×5 = 15 120 различных вариантов), но на самом деле существенно различных вариантов немного, и любой мальчишка за час может стать непобедимым чемпионом. В то же время игра в крестики и нолики имеет и более сложные разновидности, и более глубокую стратегию.

На языке теории игр крестики и нолики можно назвать конечной (то есть доигрываемой до конца за конечное число ходов) строго детерминированной (то есть не содержащей элемента случайности) игрой двух сторон с полной информацией. Последнее означает, что обоим игрокам известны все сделанные ходы. Если обе стороны играют "рационально", игра должна закончиться вничью. Единственный способ выиграть заключается в том, чтобы заманить неосторожного противника в ловушку, заготовив для следующего своего хода два почти готовых ряда (противник может помешать достроить лишь один ряд).

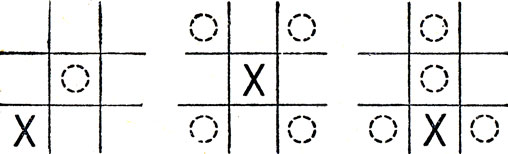
Рис. 17. Первый игрок (ему принадлежат крестики) может сделать любой из трех ходов. Во избежание проигрыша второй игрок (ему принадлежат нолики) должен в каждом случае занять лишь одну из указанных клеток

Из трех возможных начальных ходов - в угол, в центр и в боковую клетку - самым сильным является ход в угол, ибо при этом противник, чтобы не попасть с самого начала в ловушку, из восьми оставшихся клеток может выбрать только одну - центральную. Наоборот, если первый ход сделан в центр, то блокировать его можно, лишь заняв угол. Наиболее интересная партия получается в том случае, когда первый игрок, открывая игру, занимает одну из боковых клеток: при таком начале перед обеими сторонами открываются широкие возможности в постановке ловушек. Три первых хода и ответы на них второго игрока, действующего осмотрительно, показаны на рис. 17.

За много веков до нашей эры были известны гораздо более интересные с математической точки зрения варианты крестиков и ноликов, чем тот, в который принято играть в наше время. Во всех этих вариантах для игры нужно взять шесть фишек, по три у каждого игрока (у одного, например, три трехкопеечные монеты, а у другого три пятака), и доску, изображенную на рис. 18.

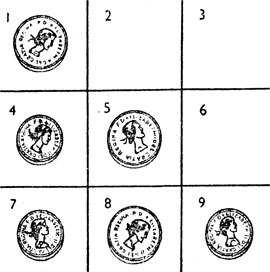
Рис. 18. Игра в крестики и нолики монетами или фишками

В древнем Китае, Греции и Риме был популярен самый простой вариант игры, когда играющие по очереди выставляют на доску фишки и делают это до тех пор, пока не выставят все шесть фишек. Если ни одному игроку не удается поставить три монеты в ряд и выиграть, то игра продолжается. Каждый из противников передвигает по очереди одну из своих фишек на соседнюю клетку. Передвигать фишки можно только по вертикали и горизонтали.

Эта игра упоминается у Овидия в книге III "Искусства любви" в числе тех игр, которыми поэт советует овладеть женщине, если она хочет привлечь к себе внимание мужчин в обществе. Игра в крестики и нолики была известна в Англии еще в 1300 гаду под названием "Танец трех мужчин", от которого пошли "танцы" девяти, одиннадцати и двенадцати мужчин; в Америке последний вариант по сей день называется "мельница". Поскольку первый игрок, начиная с центра, наверняка выигрывает, то такое начало не сулит ничего интересного и обычно им не пользуются. Это ограничение при рациональной тактике приводит к ничьей, но обе стороны могут поставить противнику уйму потенциальных ловушек.

В одном из вариантов игры разрешается передвигаться на соседние клетки вдоль двух главных диагоналей. Дальнейшее видоизменение игры (приписываемое американским индейцам) допускает перемещение любой фишки на одну клетку в любом направлении (например, с клетки 2 можно передвинуться на клетку 4). В первом варианте тот, кто делает первый ход, может добиться победы, если начнет с центра, но второй вариант, по-видимому, всегда можно свести вничью. В игре без всяких ограничений, называемой во Франции "les pendus" ("повешенные"), фишку разрешается передвигать на любую свободную клетку. Эта игра при разумной тактике также заканчивается вничью.

Известно много разновидностей крестиков и ноликов, в которых игра ведется на доске размером 4 клетки на 4. У каждого игрока имеется по четыре фишки, и их нужно попытаться выстроить в один ряд. Несколько лет назад появилась игра "тико" - разновидность крестиков и ноликов, для которой нужна доска размером пять клеток на пять. Каждый из игроков по очереди выставляет свои четыре фишки, а затем передвигает их на одну клетку в любом направлении. Выигрывает тот, кто сумеет либо поставить свои четыре фишки в ряд (по горизонтали, вертикали или" диагонали), либо выстроит их в виде квадрата на четырех клетках с общей вершиной.

Играть в крестики и нолики можно и без фишек, от этого игра не становится менее увлекательной. Рассмотрим, например, игру в крестики и нолики "наоборот" - тоу-так-тик (это название предложил М. Шоделл), Играют в нее, как в обычные крестики и нолики, но тот, кто первым закончит ряд из трех знаков, не выигрывает, а проигрывает. В игре тоу-так-тик у второго игрока имеется бесспорное преимущество. Первый может закончить вничью, лишь заняв первым же ходом центр, а в дальнейшем повторив по симметрии все ходы противника. В последние годы появилось несколько трехмерных игр типа крестиков и ноликов. В них играют на кубических досках, а выигрывает тот, кому удается занять подряд все клетки по горизонтали, вертикали или, диагонали в любом сечении куба, параллельном его грани, или на четырех главных диагоналях куба. Если куб имеет размер 3×3×3, то первый игрок побеждает без труда. Интересно заметить, что эта игра никогда не может закончиться вничью, ибо у первого игрока имеется четырнадцать разных ходов. Сделать же все четырнадцать ходов, не заполнив при этом одного из рядов по вертикали, горизонтали или диагонали, просто невозможно. Гораздо интереснее играть на кубической доске размером 4×4×4. Здесь лишь при разумной тактике ничьей может не быть.

Предлагались и другие варианты игры на кубических досках. Так, А. Барнерт придумал игру, в которой победителем считается тот, кто заполнит своими фишками клетки в любом сечении куба, параллельном одной из граней, или в шести главных диагональных плоскостях. П. Парке и Р. Саттен еще в 1941 году изобрели интересную игру на кубической доске размером 3×3×3 клетки, в которой выигрывает тот, кто сумеет занять два пересекающихся ряда. Клетку, стоящую на пересечении двух рядов, правила игры разрешают занимать в последнюю очередь. Поскольку занявший центральную клетку куба заведомо обеспечивает себе победу, этот ход разрешается лишь в двух случаях:

• если им достигается победа, то есть если все остальные клетки двух рядов, пересекающихся в центре куба, уже заняты фишками данного игрока;
• если, заняв эту клетку, играющий мешает своему противнику следующим ходом выиграть партию.

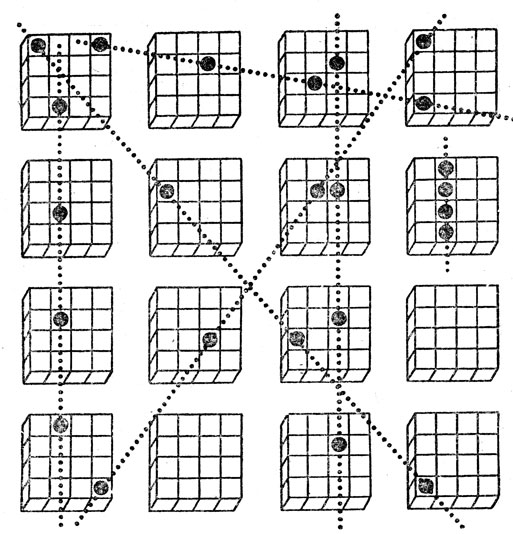
Рис. 19. Четырехмерные крестики и нолики. Пунктиром показаны некоторые ходы, приводящие к выигрышу

В четырехмерные крестики и нолики играют на воображаемой гиперкубической доске, поделив ее на двумерные квадраты. Например, гиперкуб 4×4×4×4 выглядит так, как показано на рис. 19. Выигрыш на такой доске означает, что вы сумели занять своими фишками четыре клетки, расположенные на одной прямой в любом кубе, который можно собрать из четырех последовательных квадратов, занимающих любую вертикаль, любую горизонталь или любую из главных диагоналей на рис. 19. Одно из "победных" расположений клеток изображено на рис. 20. Игрок, делающий первый ход, по-видимому, всегда может рассчитывать на победу. Если играть на гиперкубической доске 5×5×5×5×5, то игру можно закончить вничью. Число выигрышных расположений фишек при игре на n-мерной гиперкубической доске можно подсчитать по формуле, выведенной Л. Мозером:

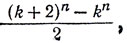
где n - размерность куба, а k - число, показывающее, сколько единиц укладывается в длине ребра куба.

Рис. 20. Куб, составленный из четырех досок 4×4

В старинной японской игре го-моку (пять камешков), и поныне не утратившей своей популярности на Востоке, используют обычную доску для игры в го (квадратная доска - 19 клеток на 19). Игроки по очереди ставят фишки на пересечение вертикальных и горизонтальных линий, разбивающих доску на квадраты, до тех пор, пока у одного из них пять фишек не окажутся расположенными на одной вертикали, горизонтали или диагонали. Каждый игрок имеет право выставлять любое число,фишек. Передвигать выставленные на доску фишки запрещается. Знатоки го-моку считают, что игрок, делающий первый ход, всегда может обеспечить себе выигрыш, но, насколько мне известно, доказательство этого утверждения нигде не публиковалось. В восьмидесятых годах прошлого века го-моку была распространена в Англии под названием го-банг. Иногда в го-банг играют на обычной шахматной доске, причем каждый игрок имеет право выставить 12 или 15 фишек. Если, выставив весь запас фишек, никто из игроков не добился победы, фишки разрешается передвигать на одну клетку в любом направлении.

В последнее десятилетие был построен ряд машин для игры в крестики и нолики. Любопытно заметить, что первый робот для игры в крестики и нолики был изобретем (хотя и не был построен еще в прошлом веке англичанином Ч. Баббеджем, одним из пионеров вычислительной техники. Баббедж намеревался выставить свою машину в Лондоне, чтобы собрать средства для проведения более важных работ, но, узнав о финансовом крахе, постигшем действовавшую в то время в Лондоне выставку "курьезных" машин (на которой среди прочих экспонатов демонстрировались "говорящая" машина и машина, сочинявшая оды на латыни), отказался от своих планов.

Выбор одного из двух одинаково выигрышных ходов робот Баббеджа производил на основе совершенно нового принципа: машина непрерывно подсчитывала число выигранных ею партий и, если ей приходилось выбирать между ходами А и В, узнавала четность текущего числа: при четном числе выигранных партий она выбирала ход А, при нечетном - ход В. Если выбор нужно было произвести из трех равных по силе ходов, робот Баббеджа делил число выигранных им партий на 3 и в зависимости от того, какой остаток получался при делении - 0, 1 или 2,- выбирал один из трех ходов. "Очевидно, что таким способом можно производить выбор при любом числе условий,- писал Баббедж.- Любознательному наблюдателю... долго пришлось бы следить за игрой робота, прежде чем он понял бы принцип, на котором основано его действие"^*.

^* (C. Babbage, Passages from the Life of Philosopher, London, 1864, pp. 467-471.)

К сожалению, после Баббеджа не осталось никаких записей о том, что он называл "простыми" механическими деталями своей машины, поэтому об устройстве ее Можно только догадываться. В его архиве сохранилась лишь запись о том, что он представляет себе такой автомат "в виде фигур двух детей, играющих друг с другом в крестики и нолики. Рядом с детьми стоят фигуры барашка и петуха. Выигравший ребенок хлопает от радости в ладоши, петух кукарекает, барашек начинает блеять, а проигравший ребенок горько плачет, заламывая в отчаянии руки". С меньшей фантазией была задумана машина для игры в крестики и нолики, демонстрировавшаяся в 1958 году на Португальской промышленной выставке в Лиссабоне: выиграв, она радостно хохотала, а проиграв (по-видимому, из-за включения специальной цепи "плохой игры"), ворчала.

Может показаться, что составление программы, позволяющей цифровой вычислительной машине играть в крестики и нолики, или конструирование для этой же цели специального вычислительного устройства - дело очень простое. И это, действительно, будет так, пока вы не захотите сконструировать робота-гроссмейстера, который выигрывал бы у неопытных игроков максимальное число игр. Трудность заключается в том, чтобы угадать, какой ход новичок сделает с наибольшей вероятностью. Разумеется, он не будет делать совсем случайных ходов, но насколько хитрым окажется новичок - неизвестно.

Чтобы вы могли получить представление о том, какие трудности здесь возникают, предположим, что новичок делает ход на клетку 8. Робот вполне мог бы ответить не слишком хорошим ходом, заняв клетку 3. При игре против знатока крестиков и ноликов такая ошибка могла бы оказаться роковой, но при игре с противником "средней квалификации" вряд ли следует ожидать, что он сразу же ответит ходом, обеспечивающим ему победу, и займет клетку 9. Четыре из шести оставшихся ходов ведут к проигрышу противника. В самом деле, у противника наверняка появится сильное искушение пойти, на клетку 4 и подстроить этим ходом роботу сразу две ловушки. К сожалению, планам противника не суждено сбыться: робот легко может избежать ловушек, ответив сначала ходом на клетку 9, а затем на клетку 5. Может оказаться, что на практике при такой довольно безрассудной игре машина будет одерживать победу чаще, чем при спокойной тактике, почти заведомо приводящей к ничьей.

Истинный мастер игры в крестики и нолики, будь то человек или робот, должен не только знать наиболее вероятные ответные ходы неопытного игрока (их нетрудно установить, собрав статистические данные об уже сыгранных партиях), но и уметь анализировать стиль игры своего партнера, чтобы определить, какие ошибки тот склонен совершать особенно часто. Следует учесть и то обстоятельство, что новичок от партии к партии совершенствует свое мастерство, но здесь "простая" игра в крестики и нолики заставляет нас погрузиться в дебри весьма нетривиальных проблем теории вероятности и психологии.

Английское название игры в крестики и нолики - тик-так-тоу - пишется и произносится по-разному. В соответствии с "Оксфордским словарем стихов Матушки-гусыни"^* название тик-так-тоу происходит от старинной английской детской считалочки:

Tit, tat, toe,
My first go,
Three jolly butcher boys all in a row,
Stick one up, stick one down,
Stick one in the old man's crown.

^* (Oxford Dictionary of Mother Goose Rhymes, 1951, p. 406. Сборники "Стихи Матушки-гусыни" соответствуют издаваемым у нас сборникам прибауток. Некоторые из "Стихов Матушки-гусыни" были переведены на русский язык С. Я. Маршаком и вышли в сборнике "Английские народные песенки".- Прим. ред.)

Я знаю многих любителей крестиков и ноликов которые ошибочно полагают, что самое главное - это научиться неизменно выигрывать, и считают, что они уже постигли все тайны этой игры. Истинный же мастер игры в крестики и нолики должен уметь использовать малейшее преимущество, возникающее даже в тяжелых для него ситуациях. Следующие три примера помогут читателю уяснить сказанное. Первый ход во всех трех партиях делается на одну из клеток 2, 6, 8, и 4

Если вы начинаете с хода ×8, а противник отвечает вам ходом О2, то вторым ходом вам лучше всего пойти на четвертую клетку (×4). Этот ход приводит к выигрышу в четырех из шести возможных ответных ходов противника. Помешать вам выиграть противник может лишь ходом О7 или О9. Если противник сначала пошел ×8, а вы ответным ходом заняли одну из нижних угловых клеток, например О9, то вы еще можете надеяться на победу: противнику достаточно совершить любой из ходов ×2, ×4 или ×7.

Если противник делает первый ход ×8, то ответный ход О5 может привести к интересному развитию партии, если противник вторым ходом занимает клетку 2 (×2), то вы можете даже позволить ему выбрать за вас ту клетку, которую вы займете при следующем ходе при любом вашем ходе выигрыш вам обеспечен.

Рассказывая о разновидности игры в крестики и нолики, любимой древними римлянами, в которой фишки разрешалось передвигать с клетки на клетку, мы упоминали о том, что игрок, заняв центр доски, всегда выиграет. Для тех читателей, кого это интересует, приводим примерный ход двух партий в древнеримские крестики и нолики.

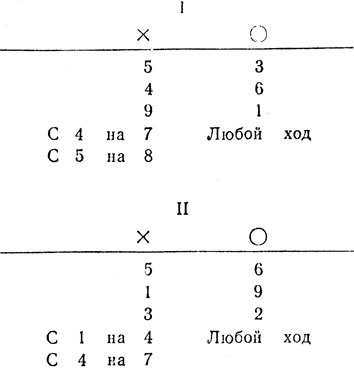
Обе партии гарантируют первому игроку выигрыш независимо от того, разрешается ли передвигать фишки по двум главным диагоналям или нет. Если фишки можно передвигать и по малым, побочным диагоналям, следует придерживаться только второй партии.