
Глава 1. Гексафлексагоны
Флексагоны - это многоугольники, сложенные из полосок бумаги прямоугольной или более сложной, изогнутой формы, которые обладают удивительным свойством: при перегибании флексагонов их наружные поверхности прячутся внутрь, а ранее скрытые поверхности неожиданно выходят наружу. Если бы не одно случайное обстоятельство - различие в формате английских и американских блокнотов,- флексагоны, возможно, не были бы открыты и по сей день и многие выдающиеся математики лишились бы удовольствия изучать их замысловатую структуру.
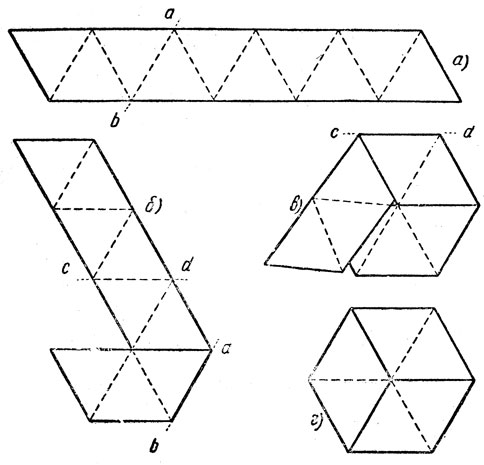
Рис. 1. Тригексафлексагон Складывают из полоски бумаги, предварительно размеченной на 10 равносторонних треугольников (а). Полоску перегибают по линии ab и переворачивают (б). Перегнув полоску еще раз по линии cd, расположим ее концы так, чтобы предпоследний треугольник оказался наложенным на первый (в). Последний треугольник нужно подогнуть вниз и приклеить к оборотной стороне первого треугольника (г). Как сгибать трифлексагоп, показано на рис. 3. Развертку трифлексагона нужно перечертить и вырезать из полоски достаточно плотной бумаги шириной около 3-4 см
Это произошло в конце 1939 года. Как-то раз Артур Х. Стоун, двадцатитрехлетний аспирант из Англии, изучавший математику в Принстоне, обрезал листы американского блокнота, чтобы подогнать их под привычный формат. Желая немного развлечься, Стоун принялся складывать из отрезанных полосок бумаги различные фигуры. Одна из сделанных им фигур оказалась особенно интересной. Перегнув полоску бумаги в трех местах и соединив концы, он получил правильный шестиугольник (рис. 1). Взяв этот шестиугольник за два смежных треугольника, Стоун подогнул противоположный угол вниз так, что его вершина совпала с центром фигуры. При этом Стоун обратил внимание на то, что, когда шестиугольник раскрывался словно бутон, видимой становилась совсем другая поверхность. Если бы обе стороны исходного шестиугольника были разного цвета, то после перегибания видимая поверхность изменила бы свою окраску. Так был открыт самый первый флексагон с тремя поверхностями. Поразмыслив над ним ночь, Стоун наутро убедился в правильности своих чисто умозрительных заключений: оказалось, можно построить и более сложный шестиугольник с шестью поверхностями вместо трех. При этом Стоуну удалось найти настолько интересную конфигурацию, что он решил показать свои бумажные модели друзьям по университету. Вскоре "флексатоны" в изобилии стали появляться на столе во время завтраков и обедов, когда вся компания собиралась вместе. Для проникновения в тайны "флексологии" был организован "Флексагонный комитет". Кроме Стоуна, в него вошли аспирант-математик Бриан Таккермен, аспирант-физик Ричард Фейнман и молодой преподаватель математики Джон У. Тьюкн.
Постоянные модели были названы гексафлексагонами: "гекса" - из-за их шестиугольной формы*, "флексагонами" - из-за их способности складываться**. Первый построенный Стоуном флексатон был назван тригексафлексагоном, так как у него были три поверхности. Вторая, не менее изящная модель Стоуна получила название гексагексафлексагона (первое "гекса" - шесть - также означает число поверхностей этой модели).
* (От греческого "гекс", что означает шесть.- Прим. перев.)
** (То flex (англ.) - складываться, сгибаться, гнуться.- Прим перев.)
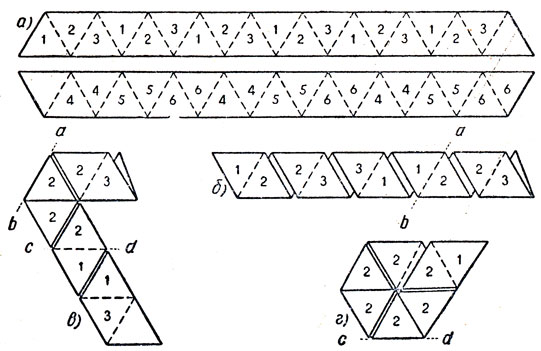
Рис. 2. Гексагексафлексагоны складывают из полоски бумаги, разделенной на 19 равносторонних треугольников (а). Треугольники на одной стороне полоски обозначены цифрами 1, 2, 3; треугольники на другой стороне - цифрами 4, 5, 6. Вместо цифр треугольники можно раскрасить в различные цвета (каждой цифре должен соответствовать только один цвет) или нарисовать, на них какую-нибудь геометрическую фигуру. Как складывать полоску, ясно из рисунка. Перегибая гексагексафлексагон, можно увидеть все шесть его разворотов
Чтобы сложить гексагексафлексагон, берут полоску бумаги (великолепным материалом для изготовления гексагексафлексагонов может служить лента от кассовых аппаратов), разделенную на 19 равносторонних треугольников (рис. 2). В треугольники с одной стороны нужно вписать в указанном на рис. 2 порядке цифры 1, 2, 3. Девятнадцатый (последний) треугольник остается незаполненным. Треугольники на обратной стороне следует в соответствии со схемой на рис. 2 пронумеровать цифрами 4, 5, 6. После этого полоску складывают так, чтобы треугольники на ее обратной стороне, имеющие одинаковые цифры, оказались наложенными друг на друга - 4 на 4, 5 на 5, 6 на 6. В результате у нас получится заготовка гексагексафлексагона, показанная на рис. 2, б. Перегнув ее по линиям ab и cd (рис. 2, в), получим шестиугольник. Остается лишь подвернуть вниз торчащий вправо пустой треугольник и приклеить его к пустому треугольнику на нижней стороне полоски. Проделать все эти операции намного легче, чем описать.
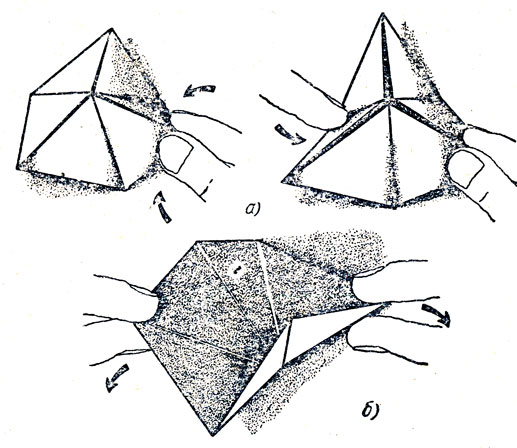
Рис. 3. Чтобы 'открыть' тригексафлексагон, его нужно одной рукой взять за два соседних треугольника, примыкающих к какой-нибудь вершине шестиугольника (а), а другой рукой потянуть за свободный край двух противоположных треугольников (б). Если флексатон не открывается, нужно попробовать ухватить его за два других треугольника. При открывании шестиугольник выворачивается наизнанку, и наружу выходит поверхность, которая ранее скрывалась внутри
Если все сделано верно, то во всех треугольниках на видимой стороне шестиугольника должна стоять цифра 1, а во всех треугольниках на другой стороне - цифра 2. В таком виде тригексафлексагон готов к перегибаниям. Взявшись за два смежных треугольника (рис. 3), согнем шестиугольник по общей стороне этих треугольников и подогнем противоположный угол флексагона. При этом откроются треугольники с цифрами 3 или 5. Перегибая флексагон наугад, вы без труда обнаружите и остальные поверхности. Однако поверхности с цифрами 4, 5 и 6 найти несколько труднее, чем поверхности с цифрами 1, 2 и 3. Иногда вы будете блуждать по замкнутому кругу: сколько бы вы ни бились, перед вами будут открываться лишь одни и те же уже успевшие надоесть вам поверхности.
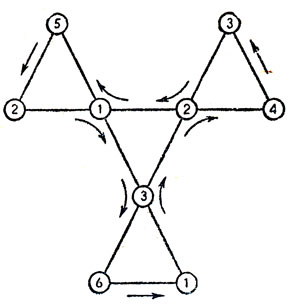
Рис. 4. Схема 'пути Таккермана' на гексагексафлексагоне
Таккерман довольно быстро нашел простейший способ выявления всех поверхностей любого флексагона: держа флексагон за какой-нибудь угол, следует открывать фигуру до тех пор, пока она "открывается", а затем, переходить к следующему углу. Этот метод, известный как "путь Таккермана", позволяет увидеть все шесть разворотов гексагексафлексагонов за один цикл из 12 перегибаний. Поверхности с цифрами 1, 2 и 3 будут появляться в три раза чаще, чем поверхности с цифрами 4, 5 и 6. Путь Таккермана удобно изображать в виде схемы, показанной на рис. 4. Стрелки указывают, в каком порядке становятся видимыми поверхности флексагона. Схемы такого типа пригодны для исследования любой разновидности флексагонов. Если модель перевернуть, то путь Таккермана будет изображаться той же схемой, но направление ее обхода будет противоположным.
Комитет обнаружил, что, удлиняя цепочку треугольников, можно делать флексагоны с 9, 12, 15 и даже большим числом поверхностей. Таккерман ухитрился даже изготовить действующую модель флексагона с 48 поверхностями! Он также обнаружил, что из зигзагообразной полоски бумаги (то есть из полоски с зубчатым, а не прямым краем) можно сложить тетрагексафлексагон (с четырьмя поверхностями) и пентагексафлексагон (с пятью поверхностями). Существует три различных гексагексафлексагона: первый складывают из прямой полоски бумаги, второй - из полоски, предварительно сложенной в виде шестиугольника, и третий - из полоски, форма которой напоминает лист клевера. Разновидностей декагексафлексагона (с девятью поверхностями) намного больше - их 82. Заготовки для всех 82 типов декагексафлексагонов имеют вид бумажных полос, сложенных самым причудливым образом. В принципе можно построить флексагон с любым числом поверхностей, но если поверхностей больше 10, то число разновидностей флексагонов катастрофически возрастает. Кстати, все флексагоны с четным числом поверхностей делаются из двусторонних полос, а флексагоны с нечетным числом поверхностей, подобно листу Мёбиуса, имеют лишь одну сторону.
Полная математическая теория флексагонов была разработана в 1940 году Тьюки и Фейнманом. Помимо всего прочего, теория указывает точный способ построения флексатона с любым числом сторон, причем именно той разновидности, которая требуется. В своем полном виде эта теория так никогда и не была опубликована, хотя отдельные ее части впоследствии были открыты заново другими математиками. Среди энтузиастов "флексологии" следует назвать отца Таккермана известного физика Луи Таккермана. Таккерман старший внес существенный вклад в теорию флексагонов, разработав простой, но эффективный способ изображать путь Таккермана в виде дерева.
Нападение японцев на Пирл-Харбор приостановило работу "Флексагонного комитета", а война вскоре разбросала всех четырех его учредителей в разные стороны. Ныне Стоун читает курс, математики в Манчестерском университете, Фейнман, известный физик-теоретик, работает в Калифорнийском технологическом институте. Тьюки занимает пост профессора математики в Принстоне, его блестящие работы по топологии и теории вероятности снискали ему мировую известность. Таккерман - видный математик, он участвовал в разработке проекта быстродействующей электронной вычислительной машины, которая была создана в Институте высших исследований.
Комитет все еще надеется как-нибудь собраться и написать одну или две статьи с подробным изложением теории флексагонов. Но пока этого не случилось, ничто не мешает нам, играя с самодельными флексагонами, попытаться вывести собственную теорию.
* * *
Прежде чем приступать к изготовлению флексагона, полезно несколько раз перегнуть в обе стороны его развертку по всем линиям сгиба. Это намного облегчает последующие манипуляции с флексатоном. Иногда читатели делали более долговечные модели, вырезав треугольники из картона или металла и соединив их липкой лентой или же наклеив на длинную полоску ткани. Между треугольниками оставались небольшие зазоры, что позволяло легко сгибать флексагоны. Таккерман старший обычно пользовался стальной пластинкой таких размеров, что, обернув вокруг нее бумажную ленту, можно быстро получать сложенную особым образом полоску, показанную на рис. 2, а. Это давало существенный выигрыш во времени при изготовлении флексагонов из линейной цепочки треугольников.
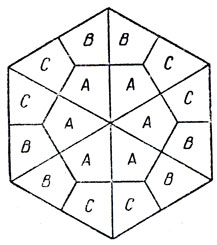
Рис. 5
Из писем читателей я узнал множество способов раскраски флексагонов, которые приводят к интересным головоломкам и самым неожиданным зрительным эффектам. Так, каждая поверхность гексагексафлексагона может появляться по крайней мере в двух различных видах в зависимости от того, как повернуты относительно друг друга образующие ее треугольники. Например, если каждую поверхность разделить на части так, как показано на рис. 5, и выкрасить области А, В и С в различные цвета, то в центре видимой поверхности могут появиться и области А (именно этой случай и показан на рис. 5), и области В, и области С. На рис. 6 изображен геометрический узор, который, будучи нарисован на одном развороте флексагона, появляется на двух других разворотах, каждый раз принимая иной вид.

Рис. 6
Вращая треугольники, из которых составлен правильный шестиугольник, мы получаем 18 различных разновидностей шестиугольников. Если гексагексафлексагон сделан из прямой полоски бумаги, то три из этих 18 шестиугольников никогда не встретятся нам, как бы мы ни складывали наш флексагон. Это навело одного из наших читателей на мысль наклеить на каждый разворот гексагексафлексагона части трех различных картинок. Перегибая определенным образом флексагон, мы будем видеть по очереди в центре открывшейся поверхности одну из картинок, а на периферии - фрагменты двух других изображений. К трем "скрытым" шестиугольникам, которые никогда полностью не появляются на видимой стороне флексатона, он приклеил разрезанные на части портреты трех очаровательных девушек, которых зритель, несмотря на все свои старания, никак не может рассмотреть во всех подробностях. Свою игрушку читатель назвал гексагексафрастрагон*. Другой читатель добился аналогичных результатов, склеив два смежных треугольника. Из-за этого исчез целый шестиугольник, и жертвы невинного розыгрыша тщетно пытались найти недостающий разворот флексагона. Неудача казалась тем более непонятной, что, заглянув внутрь флексатона, они собственными глазами видели части таинственно исчезнувшей поверхности!
* (То frustrate (англ.) - расстраивать, делать что-либо тщетным, безнадежным, обрекать на неудачу.- Прим. перев.)
Утверждение о том, что шестиугольники, возникающие при развороте гексагексафлексагонов, могут быть только 15 различных типов, необходимо несколько уточнить. Несимметричная раскраска поверхностей гексагексафлексагонов позволяет обнаружить любопытный факт: три из 15 допустимых шестиугольников имеют свои зеркально-симметричные пары. Перенумеровав внутренние углы каждого из допустимых шестиугольников по часовой стрелке цифрами от 1 до 6, мы обнаружим, что при складывании флексагонов три шестиугольника переходят в зеркально-симметричные шестиугольники, у которых углы перенумерованы теми же цифрами, но расположенными в обратном порядке. Если принять во внимание эту асимметрию, то можно сказать, что шесть поверхностей гексагексафлексагона могут порождать 18 различных шестиугольников.
Для тех, кто захочет сам изготовить флексагоны других типов, отличные от рассмотренных, мы приводим краткий обзор флексагонов низших порядков.
- Унагексафлексагон. Полоску из трех треугольников разглаживают и концы ее соединяют так, чтобы получился лист Мёбиуса с треугольным краем (более изящная модель листа Мёбиуса с треугольным краем рассматривается в главе 7). Поскольку лист Мёбиуса имеет только одну сторону и состоит из шести треугольников, его можно назвать унагексафлексагоном, хотя, разумеется, у него нет шести сторон и он не складывается.
- Дуогексафлексагон представляет собой просто шестиугольник, вырезанный из бумаги. У него две стороны, но он не складывается.
- Тригексафлексагон. Существует только одна разновидность этого флексатона, именно она и была уже описана нами.
- Тетрагексафлексагон также существует лишь в единственном варианте. Его складывают из пилообразной полоски, изображенной на рис. 7, а.
- Пентагексафлексагон. Единственную разновидность этого флексагона складывают из полоски, показанной на рис. 7, б.
- Гексагексафлексагон. Существует три различных типа этих флексагонов, каждый из них обладает неповторимыми свойствами. Мы дали описание лишь одного типа. Два остальных можно сделать из полосок, форма которых показана на рис. 7, е.
- Гептагексафлексагон. Его складывают из трех полосок бумаги, изображенных на рис. 7, г. Первую полоску можно сложить двумя различными способами, поэтому общее число возможных форм гептагексафлексагонов равно 4. Третью форму этих флексагонов конструируют из полоски бумаги, имеющей вид восьмерки с перекрывающимися частями. Это первая из фигур, которые Луи Таккерман назвал "флексагонными улицами". Поверхности этой фигуры можно перенумеровать так, что на "пути Таккермана" они будут встречаться "по порядку номеров", как дома на улице.
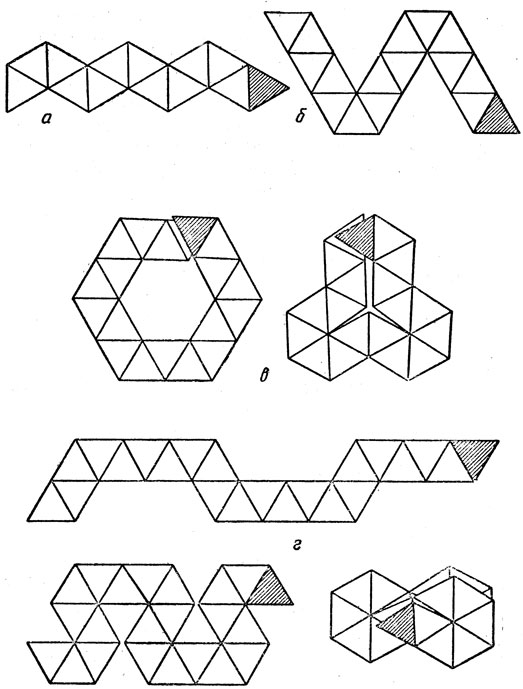
Рис. 7. Зигзагообразные полоски бумаги для складывания гексафлексагонов. Заштрихованные треугольники служат клапанами для склеивания
Существует 12 различных типов октагексафлексагонов, 27 типов эннагексафлексагонов и 82 типа декагексафлексагонов. Точное число флексагонов каждого порядка определяется неоднозначно и зависит от того, что следует понимать под "различными" флексагонами. Например, все флексагоны имеют асимметричную структуру и делятся на правые и левые, но зеркально-симметричные формы флексагонов вряд ли следует считать самостоятельными. Более подробно о числе неэквивалентных флексагонов каждого порядка можно прочитать в статье Оукли и Визнера*.
* (American Mathematical Monthly, 64, 1957, p. 143.)
Порядки гексафлексагонов, которые можно сложить из прямых полосок, поделенных на равносторонние треугольники, всегда кратны трем. Особенно легко построить одну разновидность гексафлексагонов с двенадцатью поверхностями. Для этого берут прямую полоску бумаги вдвое длиннее той, из которой мы складывали гексагексафлексагон, и "скручивают" ее так, как показано на рис. 2, б. При этом длина полоски сократится вдвое и станет равной длине гексагексафлексагонной полоски. Затем скрученную полоску нужно сложить точно таким образом, как если бы вы складывали гексагексафлексагон. В результате получится додекагексафлексагон.
Экспериментируя с флексагонами высоких порядков, полезно иметь в виду удобное правило: число слоев бумаги в двух соседних треугольных секциях всегда равно числу поверхностей данного флексатона. Интересно также отметить, что если каждую поверхность флексатона пометить каким-нибудь числом или символом и этот символ поставить на всех треугольниках, принадлежащих данной поверхности, то чередование символов на развернутой полоске будет обладать трехкратной периодичностью. Например, на лицевой и обратной сторонах развертки гексагексафлексагона, изображенного на рис. 2, цифры будут располагаться в такой последовательности:
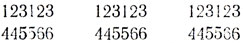
Аналогичное разделение символов на три группы характерно для всех гексагексафлексагонов, но у флексагонов нечетного порядка символы в одной из трех групп расположены в обратном порядке по сравнению с двумя остальными группами.
Из многих сотен писем, полученных мной в связи со статьей о флексагонах, я считаю наиболее забавными два. В свое время они были опубликованы в Scientific American. Вот они.
Уважаемая редакция!
Меня прямо-таки потрясла статья "Флексагоны", опубликованная в декабрьском номере вашего журнала (за 1956 год). Провозившись каких-нибудь шесть или семь часов, я с помощью сотрудников нашей лаборатории в конце концов сумел правильно склеить гексагексафлексагон. С тех пор вся наша лаборатория не перестает удивляться.
Сейчас мы встали перед проблемой. Как-то утром один из наших сотрудников, занимаясь от нечего делать складыванием гексагексафлексагона, не заметил, как кончик его галстука попал внутрь этой игрушки. При каждом последующем перегибании галстук несчастного все больше и больше втягивался внутрь флексагона. После шестого перегибания исчез сам сотрудник.
Разумеется, мы тут же начали лихорадочно перегибать флексагон, но так и не обнаружили никаких следов нашего товарища, зато мы нашли шестнадцатую поверхность гексагексафлексагона.
Возникает вопрос: должна ли вдова исчезнувшего сотрудника получить компенсацию за все время его отсутствия или же мы можем с полным основанием сразу считать его умершим? Ждем вашего совета.
Лаборатории Аллена В. Дюмона
Клифтон, штат Нью-Джерси
Сэр!
Письмо об исчезновении внутри гексагексафлексагонии сотрудника Лабораторий Аллена В. Дюмона, напечатанное в мартовском выпуске вашего журнала, помогло нам решить одну загадку.
Однажды, занимаясь на досуге складыванием гексагексафлексагона самой последней модели, мы заметили, что из него торчит кусочек какой-то пестрой материи. При последующих перегибаниях флексагона из него показался незнакомец, жующий резинку.
К сожалению, он был очень слаб и из-за частичной потери памяти не мог объяснить нам, каким образом оказался внутри флексагона. Наша национальная диета из овсянки, хэггиса* и виски поправила его здоровье. Он стал всеобщим любимцем и откликается на имя Экклз.
* (Хэггис - шотландское национальное блюдо, приготовляемое из овечьей или телячьей требухи, овсяной муки, лука и перца.)
Нас интересует, нужно ли нам вернуть его и если да, то каким способом? К сожалению. Экклза бросает в дрожь при одном лишь виде гексагексафлексагона и он решительно отказывается "складываться".
Королевский колледж науки и техники
Глазго, Шотландия
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'