Фаза III. Собственно число

Глава 8. Сколько горошин надо взять, чтобы их было 5?

В фазе II мы ввели понятия и действия, которые ваш ребенок может использовать для суждений о числе и количестве. До сих пор нужные ему слова вводились незаметно, мимоходом, так что он учился пользоваться ими в очень простых ситуациях в ходе повседневных занятий. Он научился простейшим приемам сопоставления. Он научился подбирать пары и устанавливать сходство не только предметов, их внешних форм и цвета, но также размеров и очень малых чисел. Он научился упорядочивать объекты и называть некоторые из соотношений, лежащих в основе упорядочения. К. этому времени, мы надеемся, у ребенка будет развиваться понимание количества как понятия, и он начнет усваивать, что слова такой же и больше употребимы применительно и к количеству. Он начал учиться счету вслух и знает значения нескольких малых чисел - пусть в ограниченном, но очень важном смысле.

В следующей фазе многие ПУСы являются продолжением предыдущих, но в них меняется ориентация. В фазе II каждое упражнение предлагалось ребенку в форме, которая обязывала его выполнять задания частным образом. Каждое его действие определялось конкретным заданием. Это значит, что его просили или сравнить что-то, или назвать, или расположить в определенном порядке. В фазе III ПУСы усложняются в двух отношениях. Во-первых, предлагаемый материал будет не столь прямолинейным, а во-вторых, вопросы будут формулироваться иначе. Теперь ребенок должен сам выбирать одно из известных ему действий, нужное для решения задачи, поставленной в ПУСе. Он должен усвоить, что некоторые действия являются подходящими только при определенных условиях и не годятся при других обстоятельствах. Например, если его спрашивают, одинаковы ли два ряда бусинок, то он должен усвоить, что сравнение длины рядов может не дать правильного ответа - в одном из рядов бусинки могут располагаться ближе друг к другу. Если ребенок не может определить число бусинок прямым счетом, то единственно надежным путем будет установление попарного соответствия или же счет с помощью бирок.

В предыдущей фазе ребенку было достаточно установить качественную идентичность используемых материалов; теперь же он должен осознать, что изменение только лишь внешней формы объектов не влияет на количество заключенного в них вещества. Воду можно перелить из одного стакана в другой, совершенно другой формы, шарики пластилина раскатать в колбаски, ряды бусинок растянуть, но количества останутся теми же. Количество можно изменить путем добавления или убавления материала. Ребенок должен научиться различать эти два принципиально разных действия - изменение внешнего вида и изменение количества.

Перед ним встанут более тонкие вопросы, и он окажется в более запутанных ситуациях. Ребенок будет иметь дело с вопросами: "Сколько?" и "Одинаковы ли?", причем одинаковые теперь уже не означает, что сравниваемые объекты одинаковы по виду. Это большой шаг вперед. Мы предлагаем ребенку отказаться от испытанных и надежных действий и понятий, которые он медленно усваивал, в пользу новых, более сильных действий и понятий. Некоторое время он может упорствовать и пользоваться старыми способами мышления и решения задач. Позвольте ему быть самостоятельным тогда, когда он сам сочтет нужным.

1. Опираться на то, что он уже знает

1. Овладеть небольшими числами.

Наша первая задача состоит в том, чтобы ребенок постепенно овладел малыми числами, которые он должен научиться воспринимать как нечто отдельное. Он может теперь усвоить, что 2 всегда есть 2, независимо от того, идет ли речь об автомобилях, ногах или карандашах. Поэтому его нужно вывести за рамки тех узких ситуаций, описанных в предыдущей фазе, когда его просили назвать число карандашей на столе. Это достигается путем вовлечения его в игры, в которых он должен перечислить все, что имеет 2 ноги, отметить все домики, у которых 3 окна, все горшки с одним цветком и т. п.

Вы можете составить смешанные группы предметов (из бусинок, камешков, кубиков, ракушек, шариков и т. д.) и попросить его отобрать все блюдца с 2,3,4 или 5 предметами на них. Важно, чтобы ребенок пришел к мысли, что все множества из двух элементов должны, всегда выглядеть сходными в том смысле, что двоичность есть их общее свойство. После того как ребенок освоит эту идею, важно начать говорить о том, содержат ли два множества одинаковое число элементов, или какое-то из них содержит больше, применяя эти термины к множествам (наборам) с большим числом предметов. Если ребенок может с этим справиться, хорошо говорить и о том, в каком наборе меньше предметов, но некоторые дети до 5 лет имеют трудности с этим словом и могут оперировать только со словом больше. Уместны такие игры, как "Назови животное, у которого такое же число (столько же) ног, как у собаки", "животное, у которого больше ног, чем у птицы". Спросите малыша, кому положили больше сосисок, отцу или ему. Используйте подобным образом подходящие ситуации, возникающие в повседневной жизни.

Важно также иногда спрашивать "Сколько?" и заставлять его отвечать правильно, употребляя относительно большие числа. Многие маленькие дети прекрасно справляются с заданием, когда их просят взять 2 карандаша, но вопрос, сколько у них ног или ушей, воспринимают как сигнал, чтобы начать считать вслух до того числа, до которого они могут.

Дэйвид, чуть старше 3 лет, без труда может взять 2 и даже 3 карандаша, но когда его спрашивают, сколько у него глаз, считает до 7, каждый раз касаясь лица при назывании чисел во время счета. Это иллюстрирует интересную переходную стадию счетом вслух и счетом с помощью бирок. Генри (4 г. 1 мес.) может считать вслух до 11. Когда его просят сосчитать у кого-нибудь пальцы на руках, он начинает считать бирками показанным ему способом, но иногда останавливается между 9 и 11. В другом случае, когда ему предложили положить по 5 бусинок в каждую из двух кружек, Генри правильно положил бусинки, но ошибся в счете бирками и решил, что в одну из кружек он положил 6 бусинок. На этом основании он утверждал, что кружка с 6 бирками содержит больше бусинок. Когда бусинку из этой кружки вынули, оставив только 4 бусинки, тогда он сказал, что теперь число бусинок в кружках стало одинаковым.

Мы хотим - и это еще более важно,- чтобы ребенок овладел понятием порядка в ряду чисел в той степени, в которой он может это самостоятельно проверить: 2 больше, чем 1; 3 больше, чем 2. Ребенку не обязательно говорить о "порядке в множестве чисел", он может действовать и без этой терминологии; существенное значение имеет сама идея.

Чтобы указать в наглядной форме соотношение между порядковыми и количественными числительными и заодно помочь развитию ловкости рук у ребенка, вы можете сделать или купить набор счетных палочек и колечек (см. рис. 18).

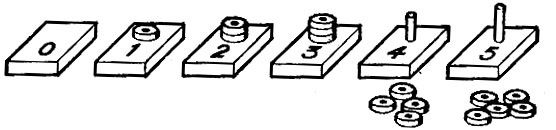
Рис. 18

Высота каждого столбика (палочки) определяет число колечек, которые на него можно надеть. Разноцветная окраска колечек даст возможность ребенку проявить изобретательность если он не будет игнорировать цветовые различия. Пройдет некоторое время, пока он заметит, что все 5 зеленых кружков насаживаются на пятый столбик, так что не остается лишних зеленых кружков и нет свободного места на столбике; что 3 красных кружка как раз заполняют третий столбик и т. д. Затем он может начать выстраивать в ряд столбики по их высоте, и, как ни странно, этот ряд оказывается также соответствующим порядку натуральных чисел и числу колечек на каждом столбике.

Действуя таким образом, ребенок придет к понятию нуля как члена числовой последовательности. Нулевая дощечка не имеет столбика, и на ней нет места для колечка. Насколько мы можем судить, не ранее чем в IX в. н. э. кому-то, вероятно индусу, пришла к голову блестящая мысль ввести специальный символ, обозначающий ничто. Возможно, вавилоняне или даже индейцы майя натолкнули индусов на мысль о призрачном столбике. Во всяком случае, эта простая идея - использовать знак, обозначающий ничто,- была неизвестна древним римлянам и не применялась в Западной Европе примерно до 1000 г. н. э. Как бы то ни было, после введения нуля все наши арифметические вычисления сильно упростились. Десятки пишутся слева от единиц, сотни - слева от десятков, тысячи - слева от сотен и т. д. Именно использование нуля как члена ряда натуральных чисел сделало возможным введение десятичных разрядов: величина, представленная цифрой, зависит от ее места в записи чисел. Эта основополагающая идея рассматривается в главе 12, где мы вводим модную теперь новую математику.

2. Развитие навыка установления попарного соответствия.

Взаимно-однозначное соответствие важно в двух отношениях. Во-первых, это основа ежедневного счета с помощью бирок. Чтобы правильно считать, ребенок должен научиться прикладывать один, и только один, числовой ярлык к каждому объекту по очереди. Во-вторых, попарное соответствие может дать ответ на вопрос, одинаково ли число предметов в двух множествах, без фактического пересчитывания предметов. Это, в частности, важно при больших числах, с которыми ваш ребенок, может быть, еще недостаточно освоился, или в ситуациях, когда некоторое количество объектов нужно распределить поровну между двумя (или более) людьми: "Один - тебе, один - мне".

Теперь для ребенка пришло время учиться собственно счету. Сначала ребенок должен научиться считать предметы, расположенные четко раздельно (чтобы он не мог ошибочно сосчитать один и тот же предмет дважды). Другой хороший прием состоит в том, чтобы брать один предмет за другим, считая их по мере появления и перекладывая затем в другое место (достаточно удаленное, чтобы исключить смешивание кучек). Позднее предложите ребенку сосчитать предметы, расположенные по кругу или образующие произвольные фигуры. На этих ранних стадиях вы можете обнаружить, что с помощью ярлыков ребенок может сосчитать только до 6 или 7, даже если умеет считать вслух до намного больших чисел. Это совершенно обычное явление, и достаточно научить его употреблять такие слова, как столько же и больше в связи со счетом бирками.

Помогите ребенку расширить умение устанавливать попарное соответствие, предложите ему разделить карандаши или шарики между двумя людьми поровну. Попросите найти для вас столько же камешков, сколько кружков изображено на домино. Наконец, испытайте его способность ответить, являются ли одинаковыми (по числу предметов) две группы (содержащие большее число предметов, чем он может сосчитать по ярлыкам), путем установления попарного соответствия. Основное, чему он учится, это то, что те же операции могут быть использованы для установления одинаковости числа или количества.

Весьма примечательно, что Линда (5 л. 2 мес), которая хотя и знает, как разложить предметы в две кружки поровну способом "один в эту кружку, один в ту кружку", но случайно ошиблась (пропустила одну из кружек во время раскладывания), затем, когда ей предложили для проверки сосчитать предметы, сознательно считала неправильно, чтобы доказать, что в обеих кружках находится одинаковое число предметов. Она уже овладела идеями попарного соответствия и счета и знала, что они должны подтверждать друг друга. Для нее это был настоящий фокус, который снова и снова доставлял ей затруднение, и она старалась как-то приспособить факты к тому, что, как она знала, должно было бы быть.

3. Развитие понятия относительного размера.

Ребенок уже познакомился со словами большой, длинный, короткий, высокий, больше, длиннее, толще и т. д., а также словами наибольший, средний и наименьший в самых простых статичных условиях, когда его просили сравнить два или три объекта. Теперь мы хотим расширить применение этих слов.

Как уже отмечалось, эти прилагательные, которые, казалось бы, отражают абсолютный размер, часто в действительности используются для относительного сравнения. Старая загадка "Какую длину имеет длинный кусок бечевки?" показывает наше отношение к трудностям этого типа. Если вы говорите о длинном куске бечевки, то этот кусок является длинным только потому, что другое кусок короче, причем длинный кусок может быть длиной всего в несколько сантиметров. Когда вы говорите о длинной и короткой дорогах, измерения могут проводиться в метрах или, скажем, километрах. То же со словом высокий: высокая банка будет меньше метра, высокий человек - больше 2 м. Иначе говоря, в языке взрослых есть скрытые предположения, которые могут быть логично пояснены, но к которым ребенок должен приспособиться самостоятельно в процессе общения. Указанные слова не обозначают чего-либо фиксированного или абсолютного в том смысле, в каком метр, грамм или час означают фиксированные величины. Некоторый предмет является длинным, или толстым, или высоким только по сравнению с нормальным размером или эталонной группой, встречающейся в повседневной жизни,- это ребенок должен постичь интуитивно. Он может учиться, только слушая, как вы используете эти слова и помогаете ему применять их правильно, не объясняя, конечно, ему логики этих любопытных условностей. Пока вы читаете эту книгу, может быть, вас удивит и заставит задуматься вопрос: "Почему короткая дорога оказывается длиннее длинной бечевки?"

То же самое со словом больше. Ребенок может легко справляться с выбором большего кубика или большей тарелки из двух кубиков или тарелок, но как он должен обращаться с еще большим кубиком? Нужно помочь ему осознать эти специфические особенности. Только таким способом можно его натолкнуть на самостоятельное обдумывание вещей. Точно так же со словами большой, средний и маленький предмет. Что происходит, когда существует еще один предмет среднего размера, чуть меньше первого? Из этого положения взрослые находят выход с помощью таких выражений, как еще больше или второй по величине.

Таким путем вы поможете вашему ребенку увидеть, что эти измерения меняются и сдвигаются и что они не означают ничего абсолютного или фиксированного. В этом заключается важная подготовка к фазе IV, где ребенок будет иметь дело с подвижными измерениями. Важно также начать привлекать внимание ребенка к тому, что предметы могут различаться в двух измерениях одновременно: они могут быть высокими и толстыми, короткими и толстыми, причем эти измерения могут сочетаться, образуя новые категории. Конечно, предметы могут различаться и тремя измерениями, но на этой ступени это для него слишком сложно и трудно.

Другое лингвистическое требование, с которым малыш скоро столкнется, если уже не столкнулся, касается использования слова меньше, применяемого не к дискретным, а к непрерывным материалам.

Особые проблемы возникают при сравнении непрерывных количеств, когда по природе вещей счет невозможен. Эти проблемы детально рассмотрены в фазе IV, Пока мы можем только занять плацдарм на этой территории, начав с оценки величин площадей, которые требуют применения счета, чтобы подкреплять суждения, сделанные просто на глазок.

Площадь является очень непростым понятием. Хотя она и не столь сложна, как объем, но и она выявляет те трудности, которые возникают при оценке количеств, не поддающихся счету или некоторым другим формам измерения. При сравнении двух площадей, скажем поверхностей крышек двух столов, маловероятно, что возникнут трудности, если один стол больше другого и в ширину, и в длину. Очевидно, что это больший стол. Но если нам требуется сравнить длинный узкий стол с квадратным, стороны которого короче длины прямоугольного стола, но длиннее его ширины, то мы встретимся с несколькими проблемами. И одна из них - как лучше сформулировать вопрос. Мы понимаем, что вопрос относится к площади. Для ребенка понятие площади как количества плоского пространства составляет проблему не только потому, что ему трудно усвоить это понятие, но также и потому, что если даже само понятие уже усвоено, сравнение нельзя провести без определенных инструментов, за исключением тех случаев, когда разница между площадями так велика, что ее можно определить на глаз.

Чтобы обойти эту трудность, мы можем использовать площади, предварительно метризованные, т. е. мы можем взять плоские фигуры простой формы, которые заранее разделены на квадратные единицы внутри их границ. Если в этих условиях используются стандартные единицы площади, то становится возможным подсчет, а для небольшого числа единиц, в пределах непосредственного восприятия, счет может оказаться даже ненужным.

Дальнейшие проблемы связаны с ориентацией поверхности. Лежащая планка выглядит иначе, чем стоящая. Более того, вначале дети склонны обращать внимание только на одно измерение, так что высокий тонкий объект они будут считать большим такого же объекта, лежащего на боку. Изменения в ориентации нужно поэтому объединить с другими изменениями, сохраняющими тождественность, которые тесно связаны с понятием сохранения. Ребенок узнает, что плоские фигуры различной формы могут иметь одинаковую площадь, а сосуды различной формы - одинаковый объем.

Как уже упоминалось, существуют два типа преобразований:

1. преобразования, которые просто изменяют внешний вид объекта, оставляя количество неизменным;
2. преобразования, увеличивающие или уменьшающие количество.

Ваш ребенок должен научиться различать эти преобразования, так как в них заключена основная проблема, встающая перед ним, когда он осваивает идею сохранения. Как только что-нибудь прибавляется к некоторой субстанции или отнимается от нее, теряется тождественность субстанции как количества. Это очень глубокая вещь. Как и в предыдущих числовых ПУСах, прежде всего следует начать работу с очень малыми числами. Сначала дайте ему поупражняться с рядом, состоящим только из 3 бусинок. Спросите ребенка, сколько бусинок в ряду, затем растяните ряд и повторите вопрос. Так как он уже знаком с такого рода вопросами из ПУСа 31, то он, вероятнее всего, ответит "три" на оба вопроса. Теперь спросите его, остались ли они такими же. Если он ответит "нет", спросите, почему. Если он ответит "потому что они теперь длиннее", согласитесь с ним и обратите его внимание на то, что бусинок по-прежнему 3, несмотря на то что ряд растянут.

Мы хотим, чтобы ребенок освоил все виды преобразований этого типа. Вернитесь к прежней форме ряда, спросив его, сколько бусинок. Если ему ясно, что тоже число означает тоже количество, продолжайте занятие, убирая одну бусинку или добавляя бусинку к ряду, и повторяйте свои действия до тех пор, пока он не станет надежно различать эти случаи - простое изменение внешнего вида количества и изменение, происходящее от добавления или убавления чего-нибудь.

В разделе 4 следующей главы детально рассмотрены различные типы преобразований. Некоторые из них включают перемещение бусинок или шариков из одной банки в другую. Это научит ребенка пользоваться операцией перемены сосудов. В случае дискретных материалов он сможет считать или субитировать, чтобы определить, изменяется ли количество при этом виде операции. Он узнает, хотя ему об этом и не будут говорить, что перемена места не влияет на перемещаемое количество.

Знание этого обстоятельства приобретает для него огромное значение в фазе IV, когда он будет овладевать понятием сохранения в более полном смысле. Воду или глину, песок речной или сахарный нельзя сосчитать, как бусинки, но, если ребенок уже знает, что переливание из сосуда в сосуд само по себе не изменяет количества, ему будет легко опираться на понятие сохранения, когда он лишится возможности применять счет для оценки количества.