О координате и проекции вектора

В школьном курсе геометрии при определении координат вектора всегда начало направленного отрезка, изображающего вектор, совмещают с началом координат, а в курсе физики это требование не обязательно. Это обстоятельство является следствием того, что вектор в курсе геометрии и физики понимается в несколько различных смыслах.

Несогласованность возникает и по использованию понятий координат и проекций вектора. В курсе геометрии восьмилетней школы вводится только первое из этих понятий, тогда как в курсе механики 8-го класса применяется понятие проекций обоих концов вектора и самого вектора на оси координат, а понятие координаты вектора отсутствует (вводятся лишь координаты точки). Все это вызывает известные трудности в практике преподавания. Для устранения их необходимо разработать единый подход к введению и применению понятий вектора, его координат и проекций. Во второй части обобщается опыт работы авторов и некоторых учителей в школе по согласованному введению понятия вектора на уроках математики и физики.

Теперь рассмотрим связи между понятиями вектора, векторной величины и направленного отрезка.

Ответить на вопрос, является ли данная величина векторной или нет, может, строго говоря, только эксперимент.

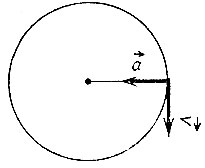
Рис.1

Часто можно встретить высказывания типа: "Так как силы - векторы (векторные величины), то они складываются геометрически". Оно принципиально ошибочно. Здесь следствие и причина меняются местами. Правильнее следует говорить: "Опыт доказывает, что для сил справедливы те же действия и их свойства, что и для векторов, значит, сила - векторная величина".

Интерпретация вектора на основе теоретико-множественной концепции (например, как параллельный перенос) порождает существенную трудность в определении отношения "равно" для векторов. В восьмилетней школе понятие равенства векторов не вводится. Однако в физике часто встречаются ситуации, при анализе которых необходимо говорить о равенстве векторных величин.

Разграничивая понятие вектора и векторной величины, говорить о том, что все действия с векторами справедливы и для векторных величин, некорректно. Такие утверждения нужно понимать правильно. Так как вектор - чисто математическое, абстрактное понятие, непосредственно не связанное с каким-либо физическим объектом, то операции с векторами имеют место для любых векторов и в применении не ограничены. Действия же с векторными величинами ограничены в применении.

Разберем примеры:

а) Шарик на нити движется по окружности в вертикальной плоскости, причем |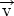| = const. На рисунке 1 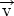- линейная скорость шарика в точке А, а - центростремительное ускорение. С точки зрения математики можно сложить любые два вектора, в том числе 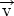и . Если же с и 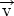связать известный физический смысл, т. е. рассматривать не как некие абстрактные векторы, а как векторные величины, то складывать их бессмысленно.

б) По третьему закону Ньютона два тела действуют друг на друга с силами, равными по своему значению и противоположными по направлению. Математика, отвлекаясь от конкретного содержания, не запрещает складывать векторы 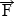₁ и 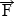₂, С точки зрения

физики это бессмысленно, так как силы приложены к разным телам и поэтому равнодействующей не имеют.

Можно привести еще примеры, которые показывают, что действия с векторными величинами, известные в математике, не охватывают все возможные ситуации, встречающиеся в физике.

Рассмотренные примеры показывают, что векторы и векторные величины не тождественные понятия, если вектор определяется отдельно (например, как параллельный перенос). Векторную величину можно измерить. Как и для скалярных величин, при выбранной единице измерения осуществляется взаимно-однозначное отображение множества Р однородных векторных величин на множество чисел R, т. е. Р→R, В результате измерений какому-либо элементу множества Р ставится в соответствие число (числовое значение величины).

4. Большие возможности практической реализации межпредметных связей математики и физики открываются в связи с изложением вопросов об измерениях величин, а в средней школе в формировании и развитии измерительных умений и навыков.

В связи с этим представляется важным обратить внимание на следующее:

1) Определение процесса измерения. Смысл этого процесса. Соотношение понятий величины и измерения.

2) Единицы измерения величин. Перевод единиц.

3) Методы измерений (прямой и косвенный).

4) Устройство и принцип действия измерительных приборов.

5) Общие правила выполнения измерений. Снятие показаний приборов.

6) Формулы для косвенного измерения величин.

7) Свойства величин, раскрывающиеся в процессе измерений.

8) Приближенный характер измерений. Виды погрешностей. Обработка и запись результатов измерений. Пути повышения точности измерений.

9) Единая трактовка некоторых метрологических понятий: эталон, мера и др.

Сравнивая процесс измерения в математике и физике, легко видеть, что они имеют много общего: 1) для измерения величины сначала выбирают единицу измерения, которая является величиной того же рода, что и измеряемая; 2) осуществляется сам процесс измерения, в результате которого находят отношение (число) измеряемой величины к единице измерения. Это число и называют числовым значением или мерой величины. Таким образом, в процессе измерения в общем случае устанавливается однозначное отображение множества однородных величин на множество действительных чисел.

Однако в целом на проблему измерения имеется две точки зрения. Согласно первой из них рассматриваемое множество объектов упорядочивают, заменяют множеством величин, затем приступают к самому этапу измерений, т, е. строят отображение множества величин на множество действительных чисел. Это отображение должно быть таково, что равным величинам соответствуют равные числа, большей величине - большее число и т. п. Чтобы упорядочить множество объектов измерения для скалярных величин, вводят бинарные отношения "больше", "меньше", "равно" и тернарное отношение "быть суммой". Эти отношения должны удовлетворять определенной группе аксиом. Векторные величины должны подчиняться аксиоматике векторного пространства.

Недостаток этой точки зрения на проблему измерения состоит в трудности заранее упорядочить множество измеряемых объектов, не прибегая к самому процессу измерения.

Согласно второй точке зрения в первую очередь элементы данного множества объектов нужно измерить (без проведения предварительного упорядочивания множества), а затем, если есть необходимость, упорядочить их. Иными словами, в этом случае имеет место непосредственное отображение множества измеряемых объектов (тел, точечное множество, свойство, явление и т. п.) на числовое множество. Это отображение означает, как и в первом случае, сравнение элемента множества объектов с единицей измерения (эталоном) и выяснение отношения (числа) данного элемента к единице измерения.

Очевидно, при второй точке зрения выпадает важное промежуточное звено - величина. При такой логике построения теории измерений величины трактуются как числа: длина, объем, площадь, масса, плотность, скорость, сила и т. п. есть числа.

О понятии величины в этом случае можно говорить лишь после изложения теории измерений.

Первая точка зрения на проблему измерений дает возможность обосновать введение той или иной величины и методов ее измерения. Действительно, вводя отношения сравнения, т. е. упорядочивая множество изучаемых объектов, мы тем самым подводим учащихся к пониманию той или иной величины и одновременно каждый раз выделяем основные признаки понятия величины. Заметим, что согласно второй точке зрения непосредственные измерения (без введения основополагающих отношений) предполагают уже известными эти отношения, что является в некотором смысле противоречием. Действительно, часто при непосредственном измерении мы должны сравнивать элементы множества объектов с единицей измерения (или эталоном), которая может быть больше или меньше этого элемента.

Как первый, так и второй подходы к проблеме измерения могут быть использованы в практике школьного обучения. В целях успешного формирования измерительных умений и навыков курсы математики и физики должны выступать единым фронтом. Причем вопрос математической обработки экспериментальных результатов должен быть одним из основных.