§ 4. Векторное пространство

Понятие векторного пространства является обобщением ряда общих свойств объектов различной природы (векторных величин, классов эквиволентных направленных отрезков, параллельных переносов и др.). Векторное пространство - это множество Р с двумя операциями, удовлетворяющими определенным требованиям. 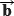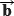Одна из этих операций каждой паре , элементов множества Р ставит в соответствие третий элемент с, который называется суммой элементов и , т. е. + 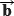= 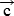. Вторая операция каждому элементу а множества Р и каждому действительному числу m ставит в соответствие элемент m множества Р, называемый произведением элемента а на число m. Обе операции должны удовлетворять следующим требованиям:

1) сложение элементов коммутативно: + = + ;

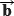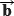2) сложение элементов ассоциативно: ( + ) + = + ( + );

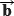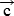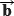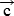3) существует нулевой элемент 0, такой, что + = ;

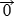4) для каждого элемента существует элемент -, такой, что + (-) = ;

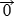5) умножение элемента на число 1 не меняет его: 1 × = ;

6) (m + n) =m + n;

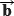7) m ( + ) = m + m;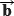

8) mn() = m(n), где m и n - числа.

Элементы векторного пространства называются векторами. Аксиомам векторного пространства удовлетворяют объекты, рассмотренные в § 2: классы эквиполентных направленных отрезков, множество параллельных переносов, множество пар точек, задающих перенос.

Эти объекты характеризуются двумя признаками: направлением и расстоянием. Однако существует много объектов, в которых эти признаки в явном виде не отражены: множество многочленов степени не выше n с действительными коэффициентами, множество квадратных трехчленов, множество линейных функций и др. Тем не менее эти множества образуют векторные пространства, элементы которых можно назвать векторами. Рассмотрим пример.

Множество линейных функций, заданных на множестве R всех действительных чисел формулой y=ax+b, образует векторное пространство. Покажем, что сумма двух линейных функций y₁=a₁x+b₁ и y₂=a₂x+b₂ есть снова функция. Действительно, y=y₁+y₂=(a₁x+b₁)+(a₂x+b₂)=(a₁x+a₂x)+(b₁+b₂)=(a₁+a₂)x+(b₁+b₂). Сложение функций коммутативно: y₁+y₂=(a₁x+b₁)+(a₂x+b₂)=(a₁x+a₂x)+(b₁+b₂) и y₂ + y₁ = (а₂x + b₂) + (а₁x + b₁) = (а₁ + а₂)x + b₁ + b₂, значит, y₁ + y₂ y₂ + y₁ и ассоциативно: (y₁+y₂)+y₃=[(a₁x+b₁)+(a₂x+b₂)]+(a₃x+b₃)=(a₁+a₂+a₃)x+(b₁+b₂+b₃) и y₁+(y₂+y₃)=(a₁x+b₁)+[(a₂x+b₂)+(a₃x+b₃)]=(a₁+a₂+a₃)x+(b₁+b₂+b₃) значит, (y₁ + y₂) + y₃ =y₁ + (y₂ + y₃).

Далее очевидно, что (аx + b) + 0 = ax + b и ах + b + [- (ах + b)] = ax + b - ax - b=0.

Линейную функцию можно умножить на число, в результате получится опять линейная функция: y - m (ax + b) = (ma)x + mb. Нетрудно убедиться, что линейные функции подчиняются остальным аксиомам, к примеру для аксиомы 6) имеем: (m + n) × (ax + b) = m (ax + b) + n(ax + b) = (ma)x + mb + (na)х + nb = [(ma)x + (na)x] + (mb + nb) = [(m + n)а]x + (m + n)b (дистрибутивность относительно сложения чисел). Таким образом, множество линейных функций с операциями сложения и умножения на число и их свойствами является векторным пространством. В таком случае линейную функцию правомерно назвать вектором.

Итак, векторное пространство является связующим понятием между объектами различной природы.

Вектор, как элемент векторного пространства, является понятием не определяемым. Те примеры, которые были рассмотрены выше, представляют собой различные интерпретации (модели) вектора, т. е. любой из рассмотренных объектов является вектором.

Логика изучения векторов зависит от того, вводится ли вектор как элемент векторного пространства или самостоятельно, вне связи с векторным пространством. При первом подходе свойства операций над векторами задаются в виде аксиом, т. е. не доказываются. При втором подходе сначала определяются операции сложения векторов и умножения вектора на число, а свойства этих операций (коммутативность, ассоциативность и др.) должны быть доказаны. Причем если в первом случае и параллельные переносы, и направленные отрезки, и векторные величины были различными интерпретациями общего понятия "вектор" (что позволяет их рассматривать с единой точки зрения как взаимосвязанные понятия), то в случае, когда вектор определяется самостоятельно, все другие понятия должны быть с ним согласованы и иметь свои определения (точные или описательные). В частности, должны быть раскрыты вопросы о том, как связаны и чем отличаются понятия вектора, направленного отрезка и векторной величины. Например, понятие "вектор" и "векторная величина" уже не могут рассматриваться как синонимы, и терминологически не совсем корректно говорить "вектор силы", "вектор скорости" и т. д., так как сила, скорость и другие векторные величины уже не суть векторы (параллельные переносы, направленные отрезки и т. д.).

Все эти вопросы важны в практике преподавания в школе, так как перед учащимися и учителями встают трудности использования знаний о векторах, известные из курса геометрии VII класса, при изучении векторных величин в физике.

Существующая в настоящее время система школьного математического образования не рассматривает концепцию векторного пространства, так как она справедливо считается трудной для учащихся средних классов и требует от них высокого уровня абстрактного мышления. Кроме того, совершенно не разработанной в настоящее время является методика использования понятия векторного пространства в курсе математики средней школы, что и не позволяет пока вводить это понятие в школе.

Все это заставляет иначе взглянуть на понятие вектора, а точнее, рассматривать его как определяемый объект внутри некоторой другой аксиоматики.

В физике и традиционных математических курсах часто вектором называют просто направленный отрезок. В этом случае остается без определения понятие направленного отрезка, что, впрочем, можно считать необязательным, т. е. вводить это понятие чисто иитуитивно, наглядно, как, например, в школьной математике вводится понятие соответствия.

Вектор можно определить и как класс эквиполентных отрезков. Однако такое определение не может быть пока использовано в школе в полной мере, так как понятия эквиполентности, эквивалентности, разбиения, класса, фактор-множества в школьном курсе математики не рассматриваются. Тем не менее некоторые из этих понятий могут быть сформированы (и фактически формируются) на интуитивном уровне.

При трактовке вектора как параллельного переноса направленный отрезок выступает лишь как удобное изображение вектора.

Запись = = 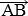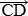означает, что речь идет о различных направленных отрезках 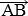и 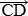, изображающих один и тот же вектор , а не о равенстве векторов. Такая трактовка вектора вызывает некоторые трудности с точки зрения приложений в физике.