§ 14. Как будет быстрее?

Важное практическое значение имеют такие задачи на движение, в которых требуется выяснить, какой из способов передвижения является наиболее выгодным в сложившейся ситуации. Например, по какой реке - с быстрым или медленным течением -можно за меньшее время проплыть туда и обратно, как лучше организовать движение, чтобы максимально эффективно использовать имеющиеся транспортные средства, и т. п.?

Не всегда такие задачи бывают просты. При исследовании ответа на поставленные ниже вопросы советуем вам вдумываться в суть дела, отыскивать причины, оказывающие основное влияние на изучаемые характеристики движения. Заметим, что для нахождения наименьшего значения какой-либо величины, скажем времени движения, необходимо не только указать само это наименьшее значение и способ его достижения, но также и доказать, что меньше полученного значения эта величина быть не может.

По дороге идут два туриста. Один из них делает шаги на 10% короче и в то же время на 10% чаще, чем другой. Кто из туристов идет быстрее?

Вы едете на автомобиле со скоростью 60 ^км/_ч. На сколько нужно увеличить скорость вашего автомобиля, чтобы проезжать один километр пути на полминуты быстрее?

По шоссе со скоростью 80 ^км/_ч движется вереница машин. Расстояние между идущими друг за другом машинами равно примерно 15 м, а средняя длина машины составляет 5 м. Можно ли в целях безопасности движения потребовать, чтобы на более узком участке дороги, скажем на мосту, машины снижали скорость до 20 ^км/_ч?

Попробуйте сообразить в уме, что быстрее: проехать весь путь на велосипеде или одну половину пути проехать на мотоцикле, двигаясь впятеро быстрее, чем на велосипеде, а другую половину пройти пешком, двигаясь вдвое медленнее, чем на велосипеде?

Что быстрее: половину пути пройти пешком, а другую половину проехать на машине или половину затраченного времени идти пешком, а другую половину ехать на машине?

Два селения расположены на одном берегу реки. Из одного селения в другое отправляется посыльный, который должен получить там пакет и возвратиться назад. Посыльный может либо пройти весь путь туда и обратно пешком, либо проплыть этот путь по реке на лодке, собственная скорость которой равна скорости пешехода.

При каком способе передвижения посыльный возвратится раньше?

Два туриста хотят добраться до селения, находящегося от них на расстоянии 30 км. Дело осложняется тем, что у них имеется только один (одноместный) велосипед. Как туристам нужно организовать движение, чтобы как можно быстрее им обоим добраться до селения? Скорость пешехода считайте равной 5 ^км/_ч, а скорость велосипедиста 15 ^км/_ч.

Три туриста хотят добраться до селения, имея только два (одноместных) велосипеда. Как туристам нужно организовать движение, чтобы как можно быстрее всем троим добраться до селения?

Могут ли три туриста, имея один двухместный мотоцикл, преодолеть расстояние 60 км за три часа? Скорость пешехода считайте равной 5 ^км/_ч, а скорость мотоциклиста 50 ^км/_ч.

Путешественник хочет пересечь пустыню по заданному маршруту, имея возможность проходить ежедневно по 20 км и брать с собой в дорогу лишь трехдневный запас продовольствия, причем только в начальной точке маршрута. В конце дневных переходов он может устраивать склады с запасами продовольствия для использования их в будущем.

За какое наименьшее количество дней при этих условиях путешественник сможет пересечь пустыню по маршруту длиной 80 км? Сможет ли он пересечь пустыню за 15 дней, если маршрут имеет длину 100 км?

Решения

14.1. Первый из упомянутых туристов идет медленнее. Действительно, когда второй турист делает 10 своих шагов длины а каждый, первый турист делает 11 своих шагов длины 0,9а каждый. Таким образом, первый турист проходит расстояние 9,9а за то же время, за которое второй проходит большее расстояние 10а.

14.2. Автомобиль, движущийся со скоростью 60 ^км/_ч, проходит один километр пути за одну минуту. Для того чтобы проезжать этот километр на полминуты быстрее, автомобиль должен за ту же минуту проезжать не один, а два километра. Поэтому его скорость должна быть вдвое больше исходной, а значит, ее нужно увеличить на 60 ^км/_ч.

14.3. Вначале скорость вереницы машин равна 80 ^км/_ч, а на каждую машину приходится участок шоссе длиной 15 + 5 = 20 м. Подъезжая к мосту, каждая из машин замедлит свое движение, но каждая следующая машина сделает это несколько позже, а значит, расстояние между машинами на мосту уменьшится. Чтобы подсчитать, на каком расстоянии друг от друга будут ехать машины, заметим, что при изменении их скоростей одна величина все же остается в среднем неизменной, а именно временной интервал между машинами, т. е. время, необходимое каждой следующей машине для того, чтобы занять место предыдущей. Поскольку на мосту скорости машин в ⁸⁰/₂₀ = 4 раза уменьшатся, то и расстояния между ними также уменьшатся в 4 раза и будут равны примерно ²⁰/₄ = 5 метрам. А так как сами машины имеют длину по 5 метров каждая, то это означает, что машины будут ехать вплотную, каковое движение практически не представляется возможным.

Из решения настоящей задачи будущие водители могут сделать для себя полезный вывод: при увеличении скорости движения машины нужно внимательно следить за расстоянием до впереди идущей машины на случай непредвиденного замедления ее скорости.

14.4. Для проезда всего пути на велосипеде потребуется меньше времени, так как столько же времени займет одно лишь прохождение половины пути пешком (с вдвое меньшей скоростью), к чему добавится время, необходимое для проезда половины пути на мотоцикле, положительное, каким бы малым оно не было (даже если скорость мотоцикла будет не в пять, а в любое число раз превышать скорость велосипеда).

14.5. Эта задача так же, как и задача 14.4, может быть решена в уме. Если идти пешком и ехать на машине одинаковое время, то путь, проделанный на машине, будет, конечно, большим, чем путь пройденный пешком. Следовательно, в этом случае на машине будет пройдено более половины всего пути, что, естественно, займет меньше времени, чем если бы на машине была пройдена ровно половина пути.

14.6. Пусть расстояние между селениями обозначено через s, скорость пешехода - через х (она же есть скорость лодки в стоячей воде), а скорость течения реки - через у. Тогда время, затраченное пешеходом на весь путь туда и обратно, равно ^2s/_x, а время, необходимое в сумме для прохождения на лодке расстояния s как по течению, так и против течения реки, равно 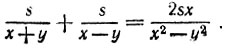Последняя величина больше, чем первая, так как

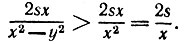
Поэтому посыльный возвратится раньше в случае, если пойдет пешком.

Казалось бы, время возвращения посыльного должно быть одинаковым при передвижении как пешком, так и на лодке: ведь течение реки половину пути относит лодку назад, а другую половину - вперед. Однако положительное действие течения длится по времени меньше, чем отрицательное, а значит, общий эффект от влияния течения реки на время возвращения посыльного будет отрицательным.

14.7. Если один турист проедет на велосипеде половину пути, т. е. 15 км, за один час, оставит велосипед и дальше пойдет пешком в течение трех часов, то он доберется до селения за четыре часа. В этом случае другой турист, наоборот, первые три часа будет идти пешком и, дойдя до велосипеда, оставшееся расстояние до селения проедет на велосипеде, т. е. тоже доберется до селения за четыре часа. Итак, оба туриста, отправившись одновременно, доберутся до селения также одновременно.

Возможны различные способы организации движения туристов, но меньше чем за четыре часа туристы никак не смогут оба добраться до селения (один из них, конечно, может добраться и за два часа, но другой при этом потратит все шесть часов). Это можно объяснить тем, что в общей сложности (в сумме) туристы должны пройти расстояние 30 + 30 = 60 км. Из этих 60 км на велосипеде можно проехать в общей сложности не более 30 км, а остальные 30 км нужно пройти пешком. Таким образом, суммарное время движения туристов не может быть меньше чем 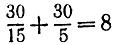часов, а, значит, если нужно, чтобы оба туриста добрались до селения одновременно, то это может произойти не ранее чем через ⁸/₂ = 4 часа.

14.8. Движение можно организовать так. Два туриста отправляются на велосипедах, а третий пешком одновременно с ними. Первый турист проезжает две трети пути до селения, оставляет велосипед и далее идет до селения пешком. Второй турист проезжает треть пути, оставляет велосипед, далее проходит еще треть пути пешком и затем едет на велосипеде, оставленном первым туристом. Наконец, третий турист проходит треть пути пешком, а затем садится на велосипед, оставленный вторым туристом, и едет на нем др селения. Таким образом, каждый турист одну треть пути пройдет пешком и две трети проедет на велосипеде, следовательно, все трое прибудут в селение одновременно.

Докажем, что быстрее туристы никак не смогут все трое добраться до селения. Действительно, в сумме три туриста должны пройти утроенное расстояние до селения, причем на велосипедах можно проехать в общей сложности не более чем удвоенное расстояние до селения, так как велосипедов только два. Поэтому суммарное время движения туристов не может быть меньше, чем время проезда на велосипеде удвоенного пути плюс время прохождения пешком однократного пути. Поделив это суммарное время на троих, мы получим как раз то наименьшее время движения каждого туриста, которое будет реализовано при указанной выше организации движения.

14.9. Могут. Движение можно организовать так. Пусть двое туристов отправляются на мотоцикле, а третий турист идет пешком. Через час один турист слезает с мотоцикла и проходит оставшиеся 10 км за два часа пешком (50 км мотоцикл уже проехал за первый час). Другой же турист возвращается на мотоцикле назад и, встретив третьего туриста, подвозит его до конечного пункта. Докажем, что эта последняя операция, связанная с возвращением назад, займет не более двух часов. В самом деле, через час после начала движения расстояние между мотоциклистом и третьим туристом равно 45 км, а расстояние между третьим туристом и конечным пунктом равно 55 км. Даже если третий турист остановится и будет просто ждать мотоциклиста, и то общее расстояние 45 + 55 = 100 км мотоциклист преодолеет за два часа. Тем более это удастся сделать, если третий турист пойдет навстречу мотоциклисту, сократив тем самым суммарный его пробег.

14.10. Пусть длина маршрута равна 80 км и A, В, С, D, Е - последовательные точки маршрута, отстоящие друг от друга на расстояние 20 км, причем А - начальная, а Е - конечная точка маршрута (рис. 46). Так как с трехдневным запасом продовольствия путешественник может пройти только 60 км, то ему придется хотя бы в одной из точек В, С или D устроить склад. Понятно, что первый раз склад может быть устроен только в точке В, поскольку, если его устроить в точке С или D, то путешественнику уже не хватит запаса продовольствия для возвращения назад в точку А за новой его порцией. Оставить в точке В он может только однодневный запас продовольствия, так как на путь от точки А до точки В и обратно путешественник тратит два дня. Если после этого он снова выйдет из точки А с трехдневным запасом продовольствия, то, дойдя до точки В и забрав находящийся там однодневный запас продовольствия, он дойдет до конечной точки Е. Итак, наименьшее количество дней, необходимое путешественнику для прохождения маршрута в 80 км, равно шести.

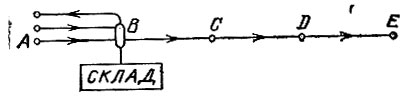
Рис. 46

Если маршрут имеет длину 100 км, то путешественник сможет пройти его за 15 дней следующим образом. За восемь дней он сделает в первой точке В, отстоящей от начальной точки А на 20 км, склад с четырехдневным запасом продовольствия. Затем путешественник заберет в точке А трехдневный запас и придет в точку В, имея там в общей сложности шестидневный запас продовольствия. Из предыдущего рассуждения в решении настоящей задачи нам известно, то за шесть дней путешественник сможет пройти 80 км. Итак, на весь путь ему понадобится 8 + 1 + 6 = 15 дней (попробуйте доказать, что менее 15 дней ему не хватит).

http://www.solnyshco.com комментариев к записи повышение иммунитета у детей.