§ 13. Измерения и вычисления в пути

С какой скоростью идет поезд или машина, какова скорость течения реки, чему равно расстояние между пунктами, не столкнутся ли два движущихся объекта? Такие вопросы часто возникают во время наших путешествий. Но вот ответы на них не всегда удается подобрать "на ходу". Мы предоставляем вам возможность в спокойной обстановке с карандашом и бумагой в руках потренироваться в решении задач подобного рода, чтобы впоследствии не испытывать затруднений в измерениях и вычислениях реальных скоростей, расстояний и промежутков времени.

При решении задач настоящего параграфа в реальных условиях вам понадобится освоить операцию измерения времени с помощью секундомера, имеющегося почти на любых часах. Полезным будет и умение измерять расстояния, скажем, шагами (см. задачу 10.1). В некоторых случаях вам поможет знание стандартных величин, таких как скорость звука, длина рельса и т. д.

Самое главное, без чего нельзя решить ни одну задачу на движение,- это понимание физического смысла движения. Мы будем молчаливо предполагать, что все объекты движутся прямолинейно и равномерно, если только в условии задачи специально не оговорено, что это не так. Важную роль будет играть идея сложения скоростей; например, скорость велосипедиста при движении против ветра будет складываться из собственной скорости велосипедиста и скорости ветра, взятой с отрицательным коэффициентом. Разумеется, такого рода предположения являются в известной степени приближенными (как, впрочем, и сами измерения), однако они позволяют хотя бы грубо оценить интересующую нас величину и исследовать ее зависимость от тех или иных параметров.

Если вы оказались во время грозы в незащищенном месте, то, наверняка, при каждом ударе грома будете испытывать известный трепет от сознания того, что где-то совсем ядом происходит грозное явление природы. Чтобы хоть немного успокоиться в описанных условиях, попробуйте определить расстояние до молнии следующим способом: сосчитайте, сколько секунд проходит между вспышкой молнии и соответствующим ударом грома; тогда, поделив полученное число секунд на 3, вы найдете искомое расстояние, выраженное в километрах. Насколько точен предложенный способ?

Представьте себе, что вы сидите за рулем автомобиля и хотите узнать скорость машины, идущей впереди вас. Как это проще всего сделать?

Находясь в движущемся поезде, вы, конечно, не раз задумывались о том, можно ли определить скорость этого поезда. Предложите какие-нибудь способы измерения скорости, разумеется, осуществимые в условиях поездки. Нельзя ли измерить скорость поезда, лежа на полке и даже не глядя в окно?

Автомобиль с грузом ехал из одного города в другой со скоростью 60 ^км/_ч, а возвращался обратно порожняком со скоростью 100 ^км/_ч. Какова средняя скорость автомобиля?

Не спешите с ответом: средняя скорость неравна ⁶⁰⁺¹⁰⁰/₂ = 80 ^км/_ч!

Поезд длиной 1 км идет со скоростью 60 ^км/_ч. Сосчитайте в уме, сколько времени понадобится поезду для прохождения тоннеля длиной 1 км.

Вы засекли время, за которое поезд прошел мимо телеграфного столба, и время, в течение которого этот поезд проходил по мосту. Затем вы определили длину моста. Как по результатам ваших наблюдений определить скорость и длину поезда?

Из окна поезда, в котором вы едете, видна гора. Можете ли вы, зная скорость поезда (см. задачу 13.3), определить высоту этой горы?

Каким образом можно измерить скорость течения реки?

По реке в обоих направлениях ходят катера, имеющие одинаковую собственную скорость. Как в этих условиях определить скорость течения реки?

Вы собираетесь проплыть на плоту по реке от одной пристани до другой. По расписанию вы узнаете, что пароход между этими пристанями не делает остановок и в одну сторону идет 3 часа, а в другую 4 часа 30 минут. Рассчитайте по этим данным, за сколько часов вы проплывете на плоту расстояние между пристанями.

Велосипедист проезжает 1 км при попутном ветре за 3 минуты, а при движении против того же ветра - за 5 минут. За сколько минут он проезжает 1 км в безветренную погоду?

На горной дороге, соединяющей два селения, нет горизонтальных участков пути. Автобус в гору всегда идет со скоростью 30 ^км/_ч, с горы 60 ^км/_ч, а на проезд туда и обратно он тратит в общей сложности 2 часа (не считая остановок). Найдите длину пути между этими двумя селениями.

Вбежав вверх по эскалатору, вы насчитали 30 ступенек, а затем, сбежав вниз по тому же эскалатору с той же скоростью относительно него, вы насчитали 150 ступенек. Сколько бы ступенек вы насчитали, пробежав в одну сторону по неподвижному эскалатору?

Пароход из порта А в порт В идет 10,5 суток. Ежедневно в полдень одним и тем же маршрутом как из порта А в порт В, так и из порта В в порт А отправляется по пароходу. Сколько пароходов встречает во время плаванья каждый из этих пароходов?

На железнодорожной линии, соединяющей пункты А и расположено несколько станций, причем на весь путь от A до В с учетом промежуточных остановок поезд затрачивает 2 часа 22 минуты. Какое наименьшее количество поездов необходимо иметь для обслуживания этой линии, чтобы с любой станции в любом направлении через каждые 20 минут отправлялся поезд?

На берегу большого круглого водоема расположены последовательно пристани A, В, С, D (рис. 44). От пристани А по направлению к пристани В отправился катер и одновременно с ним от пристани D по направлению к пристани С отправилась моторная лодка. Известно, что катер и лодка прибыли в пункты назначения также одновременно. На каком расстоянии друг от друга прошли бы катер и лодка, если бы они поменялись пунктами назначения?

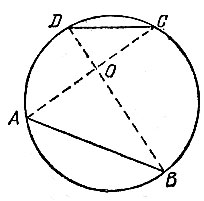
Рис. 44

Два парохода движутся по морю взаимно перпендикулярными курсами к точке О их пересечения со скоростями 30 и 40 ^км/_ч. В начальный момент расстояния от этих пароходов до точки О были равны 100 и 300 км соответственно. Найдите наименьшее расстояние между пароходами во время их движения.

Расстояние между двумя кораблями, движущимися по морю, в 6.00 ч было равно 200 км, в 13.00 ч было 150 км, а в 17.00 ч было 130 км. Каково наименьшее расстояние между этими кораблями?

Решения

13.1. Принципиальная точность предложенного метода очень высока. В отличие от света, распространяющегося практически мгновенно, звук в воздухе движется со скоростью 330 ^м/_с. Это означает, что за время, прошедшее с момента, когда раздался гром, звук прошел расстояние от молнии до наблюдателя. Так как за 3 секунды звук проходит расстояние 990 м, которое в описанных условиях вполне можно принять за 1 км, то число пройденных им километров втрое меньше числа сосчитанных секунд.

13.2. Если вы будете некоторое время ехать на постоянном расстоянии от впереди идущей машины, то ваш спидометр покажет скорость этой машины, совпадающую со скоростью вашего автомобиля.

13.3. Один из способов состоит в том, чтобы измерить время, за которое поезд проходит, скажем, 1 км, и вычислить скорость поезда, поделив расстояние на время и переведя результат в более привычные единицы ^км/_ч. Например, если поезд прошел 1 км за 72 секунды, то его скорость равна

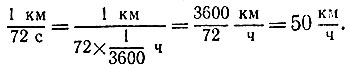
Для определения расстояния в 1 км можно воспользоваться километровыми столбиками, расположенными вдоль почти любой железной дороги.

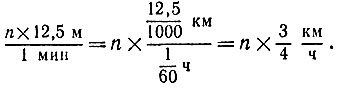
Другой способ основан на том, что, находясь в поезде, можно услышать стук колес поезда о стыки рельсов. Зная длину одного рельса, равную обычно 12,5 м, и сосчитав количество n ударов колес, скажем, за 1 мин, находим скорость поезда:

13.4. Заметим, что время, в течение которого автомобиль двигался со скоростью 60 ^км/_ч, больше, чем время, в течение которого он двигался со скоростью 100 ^км/_ч. Поэтому и "вклад" меньшей скорости в среднюю его скорость больше, чем "вклад" большей скорости, а значит, средняя скорость должна быть меньше 80 ^км/_ч. Более точно, эта мысль подтверждается определением средней скорости как отношения пройденного расстояния к времени движения. Действительно, если обозначить расстояние между городами через st то средняя скорость будет равна

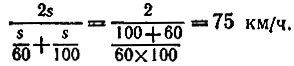
13.5. Так как скорость поезда равна 1 ^км/_мин, то через одну минуту после начала вхождения в тоннель поезд окажется расположенным полностью в тоннеле, а еще через минуту он покинет тоннель. Итого для прохождения тоннеля поезду понадобится две минуты.

13.6. Пусть за время х поезд прошел мимо телеграфного столба и в течение времени у он проходил по мосту длины в. Заметим, что время у прохождения моста можно разбить на время х прохождения всего поезда мимо начальной точки этого моста и время y-х прохождения хвоста поезда по мосту длины s. Поэтому скорость поезда, совпадающая со скоростью его хвоста, равна 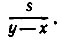Длина же поезда равна расстоянию, которое он проходит за время x, т. е.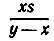

13.7. Заметим, что вид горы в окне поезда можно сравнить с ее фотографией: если зафиксировать положение глаз относительно окна, то на стекле можно произвести необходимые замеры ничуть не менее эффективно, чем на фотографии. Применим метод, который был предложен для определения высоты памятника по снимку в решении задачи 10.4. Будем исходить из того, что пропорции на стекле более или менее соответствуют реальным пропорциям горы. Выберем две точки, расположенные примерно на одной горизонтали у основания горы, и вычислим отношение расстояния между этими точками к высоте горы по результатам измерений на стекле. Найдем реальное расстояние (точнее, его проекцию на прямую, вдоль которой идет железная дорога) между выбранными точками. Это можно сделать так: засечь время, в течение которого некоторая точка на стекле проходит (по мере движения поезда) путь от одной из выбранных точек до другой, а затем умножить это время на скорость поезда. Наконец, пользуясь вычисленной ранее пропорцией, подсчитаем и реальную высоту горы.

Аналогично можно определять из окна самолета размеры, скажем, облаков, пользуясь информацией о скорости самолета, которая обычно объявляется во время полета.

13.8. Бросим какой-либо легкий предмет в реку подальше от берега (на середину) и засечем время, за которое этот предмет проплывет по течению некоторый путь, соответствующий расстоянию между двумя точками берега. Теперь, измерив это расстояние и поделив его на засеченное время, получим скорость течения реки. Можно проделать то же самое несколько раз в разных местах реки и на разном удалении от берега, а после этого найти среднее арифметическое полученных значений скорости.

13.9. Выделим участок реки, имеющий известную длину s, и засечем время движения катера по этому участку в одном и в другом направлении - пусть это будут соответственно значения х и y, причем x<y. Тогда скорость катера по течению реки равна 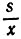, против течения 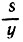, а полу разность этих скоростей 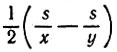равна скорости течения. В самом деле, если u - собственная скорость катера, а v - скорость течения реки, то разность скоростей по течению u + v и против течения u - v равна u + v - u + v = 2v, т. е. удвоенной скорости течения.

13.10. Если обозначить через u и v скорости парохода (в стоячей воде) и течения реки соответственно, то расстояние между пристанями будет равно, с одной стороны, 3(u + v), а с другой стороны, 4,5 (u - v). Поэтому 3(u + v) = 4,5(u - v), откуда u = 5v и s = 3*6v = 18v. Таким образом, плот проплывет это расстояние со скоростью v за 18 часов.

13.11. Скорость велосипедиста при попутном ветре, согласно условию задачи, равна - ¹/₃^км/_мин, а при встречном ветре - ¹/₅^км/_мин. Тогда собственная скорость велосипедиста равна полусумме двух указанных скоростей (см. решение задачи 13.9), а именно величине 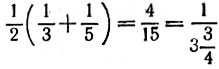^км/_мин откуда получаем, что велосипедист в безветренную погоду проезжает 1 км за 3 минуты 45 секунд (но вовсе не за 4 минуты, как может показаться на первый взгляд!).

13.12. Пусть по пути в одну сторону автобус поднимается в гору на участках одного типа суммарной длины s₁, а спускается с горы на участках другого типа суммарной длины s₂. Тогда по пути в обратную сторону он будет, наоборот, спускаться с горы на участках первого типа и подниматься в гору на участках второго типа. Поэтому на проезд туда и обратно автобус затратит в общей сложности количество часов, равное

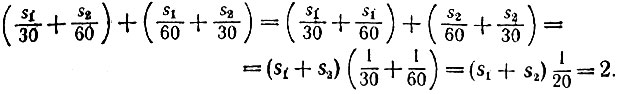
Отсюда получаем, что длина пути s₁ + s₂ между селениями равна 40 км.

13.13. Пусть эскалатор в неподвижном состоянии насчитывает х видимых ступенек. Обозначим через и нашу скорость, измеренную в таких необычных единицах, как ступеньки эскалатора в минуту, а через v скорость самого эскалатора в тех же единицах. Тогда, двигаясь в направлении движения эскалатора, вы находились на нем в течение 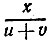минут, а двигаясь в обратном направлении,- в течение 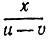минут. Поэтому вы насчитали в первый раз 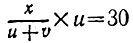ступенек, а во второй раз 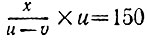ступенек. Складывая равенства

получаем 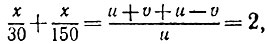откуда

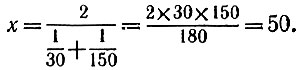
Таким образом, число видимых ступенек эскалатора в данном случае равно 50.

13.14. Данный пароход, вышедший из порта А, встретит во время плавания:

• во-первых, 10 пароходов, которые ранее вышли из порта В и еще находятся в море;
• во-вторых, тот пароход, который вышел из порта В одновременно с данным;
• в-третьих, еще 10 пароходов, которые выйдут из порта В в последующие дни.

Итого данный пароход встретит 21 пароход. Разумеется, то же самое можно сказать и о любом другом из упомянутых пароходов.

13.15. На весь путь из пункта А в пункт В и обратно один поезд затрачивает 4 часа 44 минуты, не считая стоянок на конечных пунктах A и В. За это время из начального пункта А должны отправиться еще 14 поездов, последний из которых должен выйти через 4 часа 40 минут после выхода первого поезда. Очередной поезд из пункта А должен отправиться через 5 часов после выхода первого поезда, и этот рейс может осуществить первый поезд, если он потратит на стоянки в пунктах А и В в общей сложности 16 минут. Таким образом, для обслуживания линии при данных условиях достаточно иметь 15 поездов, а меньшим числом поездов обойтись нельзя.

13.16. Пусть О - точка пересечения хорд АС и BD (рис. 44). Тогда треугольник АОВ подобен треугольнику DOC по двум углам: ∠AOB = ∠DOC (вертикальные углы) и ∠ ABD = ∠ ACD (вписанные углы, опирающиеся на одну дугу). Поэтому имеем равенство

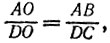
в котором правая часть равна отношению скоростей катера и лодки. Следовательно, катер и лодка проходят расстояния АО и DO соответственно за одинаковое время. Таким образом, если бы они поменялись пунктами назначения, то оказались бы в точке О одновременно, т. е. попросту столкнулись бы.

13.17. Через t ч после начального момента первый корабль будет находиться от точки О на расстоянии |100 - 30t|км, а второй -на расстоянии |300 - 40t|км. По теореме Пифагора для прямоугольного треугольника с вершинами в точках расположения кораблей и в точке О имеем, что квадрат расстояния между кораблями будет равен

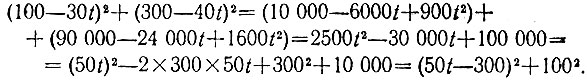
Анализ последнего выражения показывает, что наименьшее значение 100² оно принимает при t = 6, следовательно, наименьшее расстояние между пароходами равно 100 км.

13.18. Рассмотрим движение одного корабля относительно другого и заметим, что оно является равномерным и прямолинейным, поскольку таковым является движение каждого из кораблей в отдельности. Таким образом, без ограничения общности можно считать, что один корабль покоится в некоторой точке A, а другой - точка В - движется по некоторой прямой линии со скоростью v (рис. 45). Опустим перпендикуляр АС на эту прямую и обозначим через а и b расстояния от кораблей до точки С в момент t = 6. Тогда в любой момент t эти расстояния будут равны а и |b - v(t - 6)|, а квадрат расстояния между кораблями будет равен

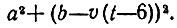
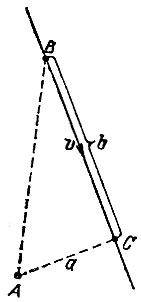
Рис. 45

Подставляя последовательно значения t = 6, t = 13, t = 17, мы получим из условия задачи три уравнения:

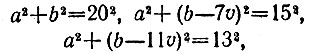
Из них находим (вычитая первое уравнение из двух других)

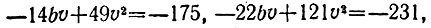
откуда v = 1, b = 16 и а = 12, последнее значение как раз и задает наименьшее расстояние 12 км между кораблями.