§ 2. Не производя деления

Вопрос о том, делится ли данное число n нацело на другое число m, часто возникает в самых разных практических задачах. Один из способов выяснить это состоит в непосредственном делении числа n на число m, однако такой способ далеко не самый легкий. Желание иметь какие-либо критерии, позволяющие устанавливать факт делимости, не прибегая к операции деления, приводит нас к задаче о нахождении наиболее простых признаков делимости.

Некоторые признаки делимости (на 2, на 3, на 5, на 9) хорошо известны. Целью настоящего параграфа является создание более или менее целостной картины, выработка единого взгляда на систему методов, дающих различные признаки делимости. Разумеется, свойства чисел настолько богаты и разнообразны, что их вряд ли можно уложить в одну простую схему, дающую все признаки делимости. Мы постарались отобрать лишь такие свойства, из которых получаются наиболее эффективные, на наш взгляд, результаты.

Для решения приведенных ниже задач могут понадобиться некоторые сведения о целых числах. Напомним, что деление числа n на число m с остатком означает нахождение частного q и остатка r, для которых выполнены условия

Если r = 0, то говорят, что число n делится на m или кратно m. Мы будем разрешать деление не только положительных чисел, но и любых целых чисел вообще - при этом число q, возможно, будет отрицательным или нулем. Будем допускать также и деление с недостатком -r, т. е. представление числа в виде

Полезно знать следующие несложные факты (если они вам не известны, то попробуйте доказать их самостоятельно):

а) если два числа отличаются друг от друга на число, кратное m, то остатки от деления этих чисел на m совпадают, и наоборот;

б) сумма двух чисел имеет тот же остаток от деления на m, что и сумма остатков от деления этих чисел на m;

в) произведение двух чисел имеет тот же остаток от деления на m, что и произведение остатков от деления этих чисел на m;

г) если произведение двух чисел, одно из которых взаимно просто с числом m, делится на m, то второе из этих чисел делится на m, и наоборот;

д) если число делится на каждое из двух взаимно простых чисел, то оно делится и на их произведение.

Число, десятичная запись которого состоит из k цифр n₁, n₂, ..., n_k-1, n_k, идущих справа налево, будем обозначать так: n_kn_k-1...n₂n₁. При этом иногда под k-значным числом будем понимать также числа, имеющие на самом деле менее k цифр, не исключая возможности, что некоторые первые цифры числа являются нулями.

Решив предложенные в этом параграфе задачи, вы сможете конструировать свои, новые признаки делимости, а также научитесь использовать свойства делимости для контроля за правильностью арифметических действий.

Сформулируйте и докажите признак делимости на 5. Как найти остаток от деления числа на 5?

Докажите, что данное число делится на 25 в том и только в том случае, если на 25 делится число, полученное из данного отбрасыванием всех его цифр, кроме двух последних. Укажите, какие в этом случае могут быть две последние цифры числа.

Сформулируйте и докажите признак делимости на 5^k при k = 1, 2, 3, ...

Сформулируйте и докажите признак делимости на 2 и вообще на 2^k при k = 1, 2, 3, ...

Согласно общему признаку делимости на 2^k, чтобы узнать, делится ли данное число на 4, достаточно проверить, делится ли на 4 число, полученное из данного отбрасыванием всех его цифр, кроме двух последних.

Как можно упростить проверку делимости двузначного числа на 4?

Согласно общему признаку делимости на 2к, чтобы узнать, делится ли данное число на 8, достаточно проверить, делится ли на 8 число, полученное из данного отбрасыванием всех его цифр, кроме трех последних.

Как можно упростить проверку делимости трехзначного числа на 8?

Докажите, что любое число при делении как на 3, так и на 9 дает тот же остаток, что и сумма его цифр.

Согласно утверждению задачи 2.7, данное число делится на 3 в том и только в том случае, если на 3 делится сумма его цифр.

Как можно упростить проверку делимости суммы цифр числа на 3, не находя самой этой суммы?

Согласно утверждению задачи 2.7, данное число делится на 9 в том и только в том случае, если на 9 делится сумма его цифр.

Как можно упростить проверку делимости суммы цифр числа на 9, не находя самой этой суммы?

Докажите, что если признак делимости на число m (большее 1) не зависит от порядка цифр делимого, то само число m может быть равно только 3 или 9.

Вы сложили несколько чисел и хотите проверить правильность своих вычислений. Для этого можно поступить следующим образом: найти остаток от деления на 9 суммы цифр полученного ответа, затем найти остаток от деления на 9 общей суммы цифр всех слагаемых. Если указанные два остатка не совпадут, то в вычислениях имеется ошибка. Дайте объяснение предложенному способу проверки сложения.

Придумайте аналогичный способ проверки вычисления алгебраической суммы, т. е. суммы нескольких целых чисел разных знаков.

Вы перемножили несколько чисел и хотите проверить правильность своих вычислений. Для этого можно поступить следующим образом: найти остаток от деления на 9 суммы цифр полученного ответа, затем перемножить остатки от деления на 9 суммы цифр каждого из сомножителей и найти остаток от деления на 9 этого произведения, Если указанные два остатка не совпадут, то в вычислениях имеется ошибка.

Дайте объяснение предложенному способу проверки умножения. Придумайте аналогичный способ проверки деления (возможно, с остатком).

В задачах 2.11 и 2.12 приведены способы проверки вычислений, которые позволяют усомниться в правильности произведенных выкладок в случае несовпадения некоторых остатков от деления на 9.

Можно ли утверждать, что если указанные остатки совпали, то вычисления не содержат ошибок?

Можно ли это утверждать при условии, что вы ручаетесь за правильность всех цифр полученного в ответе числа, кроме, быть может, одной цифры?

Вы пришли в магазин и хотите купить 8 одинаковых авторучек, несколько карандашей по 4 копейки, линейку за 9 копеек, 2 общие тетради по 18 копеек и 12 тонких тетрадей. Продавец подсчитал общую стоимость товаров и попросил вас уплатить в кассу 5 рублей 27 копеек.

Как, по-вашему, не ошибся ли продавец?

Сформулируйте признаки делимости на 6, 12, 15, 18, 24, 36, 45. Достаточно ли для проверки делимости числа на 24 установить его одновременную делимость на 4 и на 6?

Для получения признака делимости на m найдем заранее остатки m₁, m₂, m₃,... от деления на m чисел 10¹, 10², 10³,..., соответственно. Для любого числа 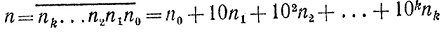определим число

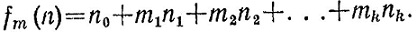
Докажите, что числа n и f_m (n) дают одинаковые остатки при делении на m и могут делиться на m только одновременно. Проверьте, что нахождение остатка m_k+1 при k = 1, 2, 3,... можно осуществить проще, если заметить, что он равен остатку от деления на m числа 10m_k, (вместо числа 10^k+1).

Проверьте, что сформулированные выше признаки делимости на 2, 3, 5 и 9 (см. задачи 2.4, 2.8, 2.1 и 2.9) представляют собой частные случаи признака Паскаля.

Получите из признака Паскаля признаки делимости на 4 и на 8. Сравните их с предложенными ранее в задачах 2.5 и 2.6.

Для практического применения признака делимости на m, сформулированного в задаче 2.16, бывает удобнее некоторые из остатков m₁, m₂, m₃,... от деления на m чисел 10¹, 10², 10³,..., Заменить соответствующими недостатками (особенный аффект от такой замены достигается в тех случаях когда недостатки близки к нулю).

Проверьте, что в результата указанной замены признак Паскаля сохранит силу.

С помощью модификации признака Паскаля (см. задачу 2.19) придумайте способ, как найти остаток от деления данного числа на 11, не производя самого деления.

Докажите, что данное число делится на 11 в том и только в том случае, если сумма его цифр, стоящих на четных местах, совпадает с суммой его цифр, стоящих на нечетных местах, или отличается от нее на число, кратное 11.

По аналогии со способами, предложенными в задачах 2.11 и 2.12, придумайте способы проверки сложения и умножения, основанные на признаке делимости на 11 (см. задачу 2.20).

Докажите, что если возможная ошибка затрагивает только одну цифру полученного в ответе числа, то наличие ошибки можно установить с помощью одного лишь признака делимости на 11.

Пользуясь модификацией признака Паскаля (см. задачу 2.19), сформулируйте признак делимости на 7.

Когда степени десятки дают при делении на m большие остатки и недостатки, эффективность признака Паскаля (см. задачи 2.16 и 2.19) оказывается невелика, поскольку подсчет значения f_m (n) в этом случае столь же трудоемок, что и непосредственное деление числа n на m. В такой ситуации существенную роль может сыграть обнаружение степени десятки, дающей маленький по модулю остаток или недостаток при делении на m, что позволяет разбить все цифры делимого на группы и тем самым действительно облегчить проверку делимости многозначных чисел.

Пользуясь тем, что число 10³ дает при делении на 37 остаток 1, получите следующий признак делимости на 37: если разбить все цифры числа n на тройки, начиная справа (в последней "тройке" может оказаться менее трех цифр, но тогда ее недостающие цифры будем считать нулями), и сложить эти тройки как трехзначные числа, то полученная сумма будет иметь тот же остаток от деления на 37, что и число n.

Придумайте способ, как упростить проверку делимости трехзначного числа на 37.

Пользуясь описанной в задаче 2.23 идеей разбиения цифр на группы, предложите признаки делимости на 7, 11, 13, сводящиеся к проверке делимости некоторого трехзначного числа на 7, 11, 13 соответственно.

Докажите, что число 10n + n₀ делится на 10m - 1 только одновременно с числом n + n₀m. С помощью этого утверждения получите признак делимости на 19.

Докажите, что число 10n + n₀ делится на 10m + 1 только одновременно с числом n - n₀m. С помощью этого утверждения получите признак делимости на 31.

Докажите, что число 10n + n₀ делится на 10m + 3 только одновременно с числом n + n₀(3m + 1). с помощью этого утверждения получите признак делимости на 13.

Докажите, что число 10n + n₀ делится на 10m - 3 только одновременно с числом n - n₀(3m - 1). С помощью этого утверждения получите признак делимости на 17.

Решения

2.1. Число делится на 5 в том и только в том случае, если его последняя цифра равна 0 или 5. Действительно, если последняя цифра числа n равна n₀, то само число n имеет вид 10n₁ + n₀. Так как число 10n₁ делится на 5, то остаток от деления числа n на 5 совпадает с остатком от деления на 5 цифры n₀. Поэтому остаток от деления числа на 5 равен нулю в том и только в том случае, если его последняя цифра делится на 5, т. е. равна 0 или 5.

2.2. Запишем данное число n в виде 100n₁ + n₀, где n₀ - двузначное число, образованное двумя последними цифрами числа n. Так как число 100n₁ делится на 25, то остаток от деления числа n на 25 равен остатку от деления на 25 числа n₀. Следовательно, число n делится на 25 в том и только в том случае, если остаток от деления числа n₀ на 25 равен 0, т. е. если две последние цифры числа n образуют одну из четырех комбинаций 00, 25, 50 или 75.

2.3. Число n делится на 5^k в том и только в том случае, если на 5^k делится число n₀, полученное из числа n отбрасыванием всех его цифр, кроме k последних. Действительно, запишем число n в виде 10^kn₁ + n₀. Тогда число 10^kn₁ делится на 5^k, а значит, остатки от деления чисел n и n₀ на 5^k совпадают и, стало быть, могут равняться 0 только временно.

2.4. Число n делится на 2^k в том и только в том случае, если на 2^k делится число n₀, полученное из числа n отбрасыванием всех его цифр, кроме к последних. Данное утверждение следует из представления числа n в виде 10^kn₁ + n₀ и того факта, что число 10^kn₁ делится на 2^k.

2.5. Проще всего в данном двузначном числе выделить наибольшее возможное четное число десятков (ведь любое число, кратное 20, кратно и 4), в результате чего останется число, меньшее 20, для которого проверка делимости на 4 уже не представляет труда. Например, число 76 = 60 + 16 делится на 4, а число 94 = 80 + 14 не делится.

2.6. Заметим, что любое четное число сотен делится на 8, а нечетное дает при делении на 8 остаток 4 и недостаток - 4. Поэтому, отбросив цифру сотен данного трехзначного числа, достаточно проверить, делится ли на 8 оставшееся двузначное число в чистом виде, если цифра сотен была четной, либо предварительно увеличенное или уменьшенное на 4, если цифра сотен была нечетной. Кроме того, для упрощения проверки делимости на 8 двузначного числа можно выделить в нем наибольшее возможное число десятков, кратное 4, в результате чего останется число, меньшее 40, для которого проверка делимости на 8 уже не представляет труда. Например, число 692 не делится на 8, так как 92 = 80 + 12 не делится на 8, а число 568 делится на 8, так как 68 - 4 = 64 делится на 8.

2.7. Пусть данное число n имеет вид

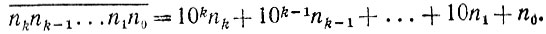
Поскольку 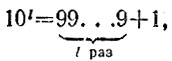то получаем

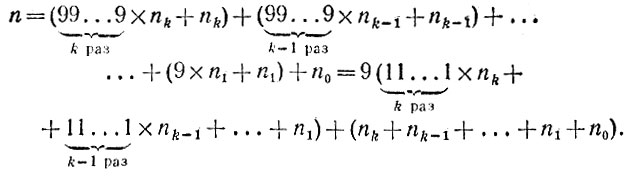
В полученном представлении числа n первое выражение делится как на 3, так и на 9, поэтому остатки от деления числа n и суммы всех его цифр n_k + n_k-1 + ... + n₁ + n₀ как на 3, так и на 9 совпадают.

2.8. Для упрощения проверки делимости суммы цифр данного числа на 3 можно заменять цифры их остатками или недостатками от деления на 3. Например, сумма цифр числа 2 795 438 дает тот же остаток при делении на 3, что и сумма 2 + 1 + 0 - 1 + 1 + 0 - 1 = 2.

2.9. Для упрощения проверки делимости суммы цифр данного числа на 9 можно отбрасывать те цифры, которые в сумме дают 9 или 18. Например, сумма цифр числа 7 543 782 861 дает тот же остаток при делении на 9, что и число 6, поскольку сумма всех остальных цифр (7 + 2) + (5 + 4) + (3 + 7 + 8) + (8 + 1) кратна 9.

2.10. Пусть число m k-значное. Тогда среди чисел от 10^k+1 до 10^k+1 + m хотя бы одно число делится на m. Это число имеет вид 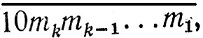, а так как признак делимости на m не зависит от порядка цифр делимого, то числа и 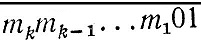также кратны m. Поэтому число m является делителем разности этих чисел, равной 9, а значит, либо m = 3, либо m = 9 (случай m = 1 исключен в условии задачи).

2.11. Описанная в задаче проверка сложения основана на том, что если при подсчете суммы нескольких чисел не было сделано ошибки, то эта сумма должна давать тот же остаток при делении на какое-либо число m, что и сумма остатков от деления слагаемых на m. При этом нахождение остатков от деления на m = 9 по сумме цифр не требует серьезных усилий, что и нашло отражение в предложенном способе. Если складывались числа разного знака, то сумма всех положительных слагаемых должна давать тот же остаток при делении на m, что и сумма всех отрицательных слагаемых вместе с полученным в ответе числом. Для нахождения этих остатков при m = 9 достаточно заменить сами числа суммами их цифр.

2.12. Описанная в задаче проверка умножения основана на том, что если при подсчете произведения нескольких чисел не было сделано ошибки, то это произведение должно давать тот же остаток при делении на m (в задаче взято m = 9), что и произведение остатков от деления сомножителей на m. Проверка деления числа а на число b, в результате которого получены частное q и остаток r, сводится к проверке равенства

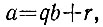
т. е. двух операций сразу: умножения и сложения. Это можно сделать, сравнив остатки от деления на m числа а и числа qb + r, в котором каждое из чисел q, b и r можно заменить остатком от деления на m. Если остатки не совпадут, то в вычислениях имеется ошибка.

2.13. Совпадение остатков от деления двух чисел на 9 не дает возможности утверждать равенство самих этих чисел: например, числа 49 и 40 имеют одинаковые остатки, но не совпадают друг с другом. Поэтому описанные в задачах 2.11 и 2.12 способы проверки вычислений не могут дать гарантии от ошибок. Та же пара чисел показывает, что даже в случае правильности всех цифр ответа, кроме, быть может, одной, этих проверок, вообще говоря, не достаточно (исключение составляет случай, когда в ответе нет ни одной цифры 0 и 9, поскольку тогда любое изменение одной цифры ответа влечет за собой изменение его остатка от деления на 9).

2.14. Если бы линейка стоила на 1 копейку дешевле, то общая стоимость товаров, выраженная в копейках, была бы кратна 4, так как в этом случае стоимость каждого вида перечисленных в условии предметов делилась бы на 4. Поскольку названа сумма 5 рублей 27 копеек, то число 27 - 1 = 26 должно делиться на 4 (см. задачу 2.5), что неверно. Таким образом, сумма подсчитана с ошибкой.

2.15. Представим данные числа в виде 6 = 2*3, 12 = 4*3, 15 = 3*5, 18 = 2*9, 24 = 8*3, 36 = 4*9, 45 = 9*5 и воспользуемся следующим утверждением: делимость на число m = pq, представляющее собой произведение взаимно простых чисел р и q, равносильна одновременной делимости на р и на q. Взаимная простота чисел р и q играет существенную роль, поскольку без этого требования утверждение было бы неверно. Например, несмотря на справедливость разложения 24 = 4*6, из делимости числа 12 на 4 и на 6 не следует его делимость на 24. В то же время делимость какого-либо числа на 8 и на 3 влечет за собой его делимость на 24.

2.16. Пусть q₁, q₂, q₃, ... - частные от деления на m чисел 10¹, 10², 10³, ... соответственно с остатками m₁, m₂, m₃, ... Тогда справедливо представление

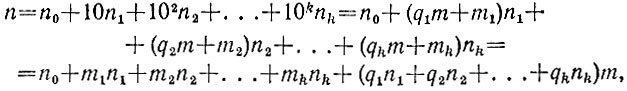
из которого следует, что числа n и

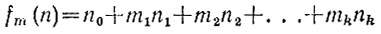
дают одинаковые остатки при делении на m. Кроме того, если при последовательном вычислении остатков m₁, m₂, m₃, ... уже найден остаток m_k, то остаток от деления на m числа

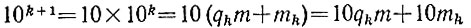
равен остатку от деления на m слагаемого 10m_k в последней сумме.

2.17. Полагая в признаке Паскаля m = 2, m = 3, m = 5 и m = 9, получаем для (k+1)-значного числа п следующие числа:

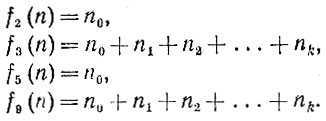
Эти числа определяют в точности те же признаки делимости, что и сформулированные в задачах 2.4, 2.8, 2.1, 2.9.

2.18. Полагая в признаке Паскаля m = 4 и m = 8, получаем для k-значного числа n следующие числа:

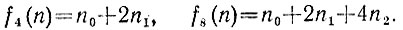
Получаемые в результате признаки делимости на 4 и на 8 несколько отличаются от приведенных в задачах 2.5 и 2.6, однако вряд ли могут рассматриваться как более простые, поскольку, на наш взгляд, требуют чуть больше вычислений.

2.19. Доказательство модификации признака Паскаля, по существу, ничем не отличается от доказательства, приведенного в решении задачи 2.16. Разница состоит лишь в том, что деление каких-то из чисел 10¹, 10², 10³, ... на m нужно провести не с остатком, а с недостатком, т. е. в соответствующих формулах

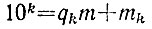
положительные числа m_k взять на m меньшими прежних (отрицательными), a q_k - на 1 большими прежних.

2.20. Производя в признаке Паскаля деление степеней десятки на 11 попеременно то с остатком, то с недостатком, имеем

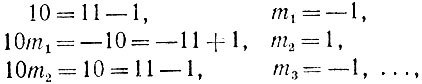
откуда получаем, что число 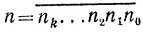дает тот же остаток при делении на 11, что и число

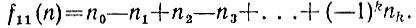
Поэтому для делимости числа n на 11 необходимо и достаточно, чтобы суммы n₀ + n₂ + ... и n₁ + n₃ + ... отличались друг от друга на число, кратное 11.

2.21. Подставляя значение m = 11 в утверждения, сформулированные в решениях задач 2.11 и 2.12, и используя признак делимости на 11, получаем способы проверки сложения и умножения. Если у числа n, представляющего собой истинный ответ, заменить одну цифру на неверную, то число f₁₁(n) обязательно изменится на некоторое число, меньшее 11 (даже меньшее 10), а значит, будет давать другой, уже неверный остаток от деления на 11. Поэтому, сравнив его с верным остатком, можно обнаружить ошибку. Более того, если известно, в какой именно цифре числа n возможна-ошибка, эту цифру можно однозначно восстановить.

2.22. Действуя согласно модифицированному признаку Паскаля, при m = 7 имеем

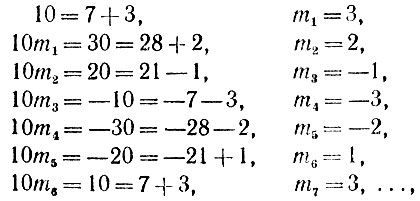
откуда получаем, что число 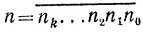дает тот же остаток при делении на 7, что и число

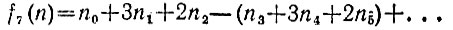
2.23. Пусть все цифры числа n разбиты на тройки, образующие трехзначные числа n₀, n₁, n₂, ..., n_k (начиная справа). Тогда число

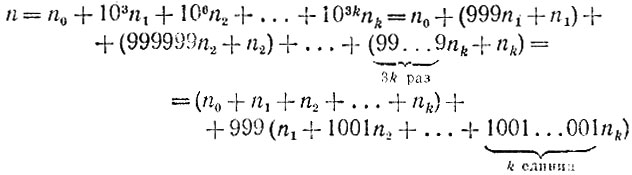
дает при делении на 37 тот же остаток, что и сумма n₀ + n₁ + n₂ + ... + n_k, поскольку в полученном представлении числа n второе выражение делится на 999 = 37*27. Если указанная сумма является более чем трехзначным числом, то к ней можно применить те же рассуждения, что и к исходному числу n, и этот процесс можно продолжать до тех пор, пока не получится трехзначное число. Наконец, любое трехзначное число 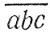сводится к двузначному переходом к разности чисел 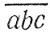и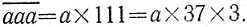

2.24. Учитывая равенство 1001 = 7*11*13, получаем, что недостаток m₁ при делении числа 103 (на любое из чисел 7, 11, 13) равен -1. Остаток m₂ от деления числа 10³ равен остатку от деления числа 10³m₁ = -1000 = -1001 + 1, т. е. равен 1. Недостаток m₃ от деления числа 10⁶, равен недостатку от деления числа 10³m₂ = 1000 = 1001 - 1, т.е. равен -1, и т. д. Поэтому если все цифры числа n разбиты на тройки, образующие трехзначные числа n₀, n₁, n₂, n₃, ..., n_k (начиная справа), то число

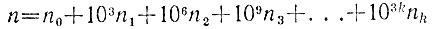
дает при делении на любое из чисел 7, 11, 13 тот же остаток, что и число

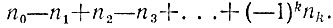
Такие же рассуждения можно применить к указанной сумме еще и еще раз до тех пор, пока не получится трехзначное число (возможно, отрицательное). Остаток от деления этого числа на 7, 11, 13 будет таким же, как и у исходного числа n.

2.25. Заметим, что число 10m - 1 не имеет общих делителей с числом 10, так как око не делится ни на 2, ни на 5. Поэтому число n + n₀m делится на 10m - 1 тогда и только тогда, когда на 10m - 1 делится число

т. е. когда на 10m - 1 делится первое выражение 10n + n₀ в полученном представлении. Полагая в доказанном утверждении m = 2, получаем, что число 10n + n₀ делится на 19 только одновременно с числом n + 2n₀. Таким образом, мы имеем следующий признак делимости на 19. В данном числе 10n + n₀ отбросим последнюю цифру n₀ и, удвоив ее, прибавим к числу я, составленному из остальных цифр исходного числа. Проделав эту процедуру несколько раз, придем к не более чем двузначному числу, которое будет делиться на 19 в том и только в том случае, если на 19 делилось исходное число. Например, для числа 3 086 379 получаем последовательность чисел 308 655, 30 875, 3097, 323, 38, последнее из которых, а значит, и исходное кратно 19.

2.26. Так как число 10m + 1 взаимно просто с числом 10, то число n - n₀m делится на 10m + 1 только одновременно с числом

т. е. одновременно с числом 10n + n₀. Полагая в доказанном утверждении m = 3, получаем следующий признак делимости на 31. В данном числе 10n + n₀ отбросим последнюю цифру n₀ и, утроив ее, вычтем из числа n, составленного из остальных цифр исходного числа. Повторяя эту процедуру, мы придем к не более чем двузначному числу (возможно, отрицательному), которое будет делиться на 31 только одновременно с исходным числом. Например, для числа 2 886 379 имеем последовательность чисел 288 610, 28 861, 2883, 279, 0, последнее из которых, а значит, и исходное кратно 31.

2.27. Число 10m + 3 не имеет общих делителей с числом 10, так как оно не делится ни на 2, ни на 5. Поэтому число n + n₀(3m + 1) делится на 10m + 3 только одновременно с числом

т. е. одновременно с числом 10n + n₀. Полагая m = 1, получаем признак делимости на 13, согласно которому, отбросив в данном числе последнюю цифру n₀ и прибавив учетверенную (3m + 1 = 4) эту цифру к числу n, составленному из остальных цифр исходного числа, получим число, которое будет делиться на 13 только одновременно с исходным числом. Учитывая признак делимости на 13, описанный в задаче 2.24, мы рассмотрим указанную схему лишь в применении к трехзначным числам. Например, для числа 481 последовательно получаем числа 52, 13, последнее из которых, а значит, и исходное кратно 13.

2.28. Так как число 10m - 3 взаимно просто с числом 10, то число n - n₀(3m - 1) делится на 10m - 3 только одновременно с числом

т. е. одновременно с числом 10n + n₀. Полагая m = 2, получаем признак делимости на 17, согласно которому, отбросив в данном числе последнюю цифру n₀ и вычтя упятеренную (3m - 1 = 5) эту цифру из числа n, составленного из остальных цифр исходного числа, мы получим число, которое будет делиться на 17 только одновременно с исходным числом. Например, применяя эту процедуру несколько раз к числу 1067 481, последовательно получим числа 106 743, 10 659, 1020, 102,0, последнее из которых, а значит, и исходное, делится на 17.