
Два великих "Д"
Все громче поют ступеньки, все явственней хруст накрахмаленных юбок. Сейчас скрипнет тяжелая створка, и в комнату войдет она, девочка, испуганно льнувшая к материнским коленям в тот тревожный овернский вечер: Жильберта Паскаль, нет Жильберта Перье, теперь уже и сама счастливая мать одного, а то и двух младенцев. Вот она у порога. Вот поворачивается медная, жарко начищенная дверная ручка...
Трах! Что такое? Комната исчезает, и глаза филоматиков с размаху упираются в кровлю интендантского дома. Несносный бес! Дразнит он их, что ли? Если так пойдет дальше, об автографе Паскаля можно забыть.
Изложив этот свой мрачный прогноз, Мате погружается в гробовое молчание, где и пребывает довольно долго, вопреки адским стараниям Асмодея извлечь его оттуда и восстановить дипломатические отношения. Измученный бес совсем было отчаялся в успехе, но тут у него мелькает счастливая мысль.
- Наидрагоценнейший, наиобразованнейший, наивеликодушнейший мсье Мате! - сладко поет он. - Окажите милость бедному черту. Я, как вы знаете, не профессиональный математик. У меня другая специальность... кха, кха! Так вот, не объясните ли вы подробнее, в чем смысл расхождений между двумя великими "Д"? Я хочу сказать, между Декартом и Дезаргом.
- Де, де! То есть да, да! - присоединяется Фило. - Я тоже не очень в этом разобрался.
- Что ж тут разбираться? - хмурится Мате (как и предполагал Асмодей, он, конечно, не устоял перед соблазном поболтать о математике).- Вы же слышали: Дезарг признавал геометрию в чистом виде, Декарт алгебраизировал ее.
- Но какой из двух методов лучше? - допытывается Фило.
- Гм... Ну, если говорить о методе Декарта, то это прежде всего метод совершенно универсальный. Пользуясь им, большинство геометрических задач можно решить с помощью элементарной алгебры. А лет эдак через тридцать, когда появится дифференциальное и интегральное исчисление, возможности аналитической геометрии Декарта станут и того больше...
- Э, нет! - протестует Фило. - Вы уклоняетесь от прямого ответа. Помнится, вас спрашивали, чей метод лучше? Декарта или Дезарга?
- Хуже, лучше... Все это понятия относительные. Что лучше: пароход или самолет?
- Вы меня спрашиваете? - уточняет Фило. - Лично я предпочитаю такси.
- Такси - городской транспорт, а я говорю о междугородном.
- Ну, тогда все зависит от обстоятельств. Если едешь в очередной отпуск, нет ничего приятнее речного теплохода. Если же в срочную командировку - тут уж необходим самолет.
- Видите, - говорит Мате, - все, стало быть, зависит от сферы применения. То же и с методами двух "Д". Удивительно красивый, хоть и сложноватый, способ Дезарга имеет неоспоримые преимущества при решении задач практических: в землемерии, в инженерном деле... Кстати сказать, Дезарг и сам отличный военный инженер.
- Как же, как же! - сейчас же вклинивается бес. - Участник знаменитой осады Ла Рошели*.
* (Ла Рошель - город во Франции. С XVI века - оплот гугенотов. В 1628 году осажден и взят королевскими войсками под началом кардинала Ришелье.)
- Вот я и говорю, - продолжает Мате, будто не слыша, - в инженерном деле без чертежей не обойтись. Подсуньте токарю алгебраическое уравнение вместо вычерченной во всех проекциях детали - он вас так поблагодарит, что не обрадуетесь! В этом случае метод Дезарга, усовершенствованный в восемнадцатом веке другим французским ученым, Мбнжем, не то что лучший, а просто-напросто единственно возможный. Если же говорить о теоретической или так называемой чистой математике - здесь уже уместнее способ Декарта.
- Ко-ко-ко! - вкрадчиво кудахчет черт. - Как говорится, Декарту и карты в руки!
Но Мате и бровью не ведет.
- Допустим, - говорит он, - нам дан воображаемый треугольник, и мы должны выяснить все, что с ним связано: площадь, размеры сторон, углов, биссектрис, высот, медиан, радиуса вписанного и описанного кругов, в свою очередь - их площади, а также длины их окружностей - словом, всю подноготную! Так вот, методом Декарта все это можно вычислить без единого чертежа, зная всего лишь координаты трех вершин, то есть шесть чисел.
Фило потрясен. Этот Декарт - настоящий фокусник! Выходит на сцену почти с пустыми руками, не имея ничего, кроме трех точек, а через несколько минут все кругом завалено биссектрисами, медианами и всякими там вписанными и описанными окружностями... Ну, а Дезарг? Как вычислял эти штуковины он?
Два великих 'Д'
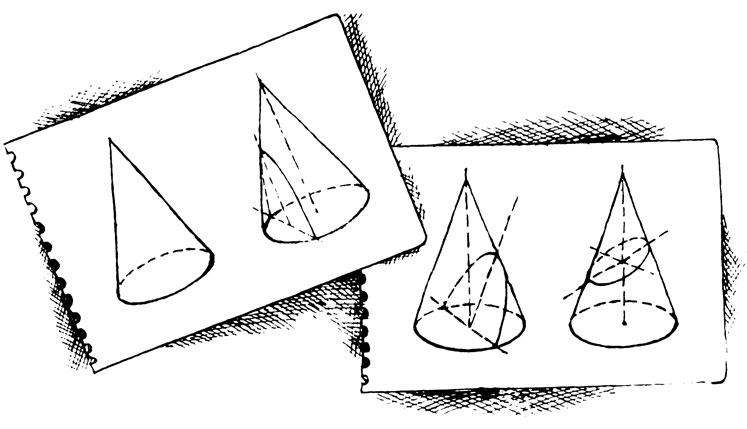
Оказывается, никак. Он вообще ничего не вычислял - только чертил. Проектировал разные геометрические тела и фигуры на всевозможные поверхности и изучал свойства проекций (оттого-то геометрия его и называется проективной). Возьмет, например, конус, проведет через его вершину различные плоскости, спроектирует на них круговое сечение конуса и исследует, что у него получилось.
Но Фило уже вошел во вкус, и общие слова его не устраивают. Он непременно хочет знать, что именно получилось у Дезарга, и услыхав, что это окружность, эллипс, парабола и гипербола, впадает в тихое умиление. Подумать только! То самое, что они проходили на исфаханском базаре!
- По-моему, мы там проходили мимо верблюда, - острит Мате.
Но Фило не до шуток. Неужели Мате не помнит? Они брали бумажный фунтик, то есть конус, и рассекали его воображаемыми плоскостями. При этом у них, совсем как у Дезарга, тоже получались окружность, эллипс, парабола и гипербола.
- Вся штука в том, что Дезарг добывал их другим способом: с помощью проекций. Понимаете?
- Вполне! Кстати, что такое проекция?
Мате закатывает глаза с видом мученика. Не знать, что такое проекция! Бывает же... Что ж, придется объяснять. Но вот вопрос: где? Сказать по правде, ему еще не доводилось чертить, кувыркаясь в воздухе.
- Знаете что? Давайте посидим на той крыше! - вдохновенно предлагает Фило. - Она вроде бы не такая покатая.
- Удачнейший выбор, мсье! - живо откликается бес, который и сам не прочь отдохнуть. - Крыша руанской судебной палаты. Самое подходящее место, чтобы судить о чем бы то ни было, в том числе о достоинствах метода Дезарга. Ко-ко...
Через минуту они уже сидят на твердой черепичной почве, для удобства покрытой асмодеевым плащом.
- Может, позавтракаем? - осторожно заикается Фило.
- Вы, кажется, проекциями интересовались, - обрывает его Мате и лезет за своим блокнотом. - Начнем с проекции, которая называется центральной.
Он набрасывает контур некой произвольной фигуры, на некотором расстоянии от нее обозначает плоскость...
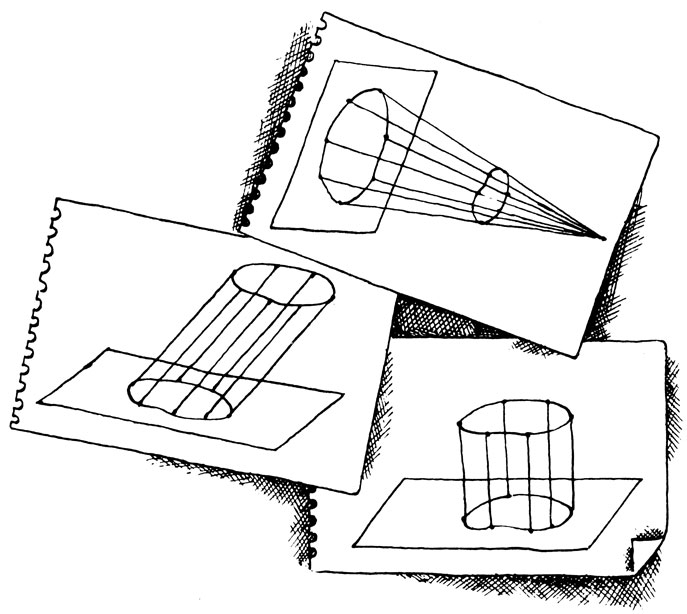
- Допустим, нам надо спроектировать вот эту фигуру на эту вот плоскость. Выберем точку вне заданной фигуры - назовем ее центром проекций - и проведем из нее лучи через точки контура до пересечения с плоскостью. Точки пересечения объединим одной линией - и проекция готова.
- Как просто! - удивляется Фило. - К тому же очень похоже на то, что мысленно делает художник, когда хочет изобразить предмет в перспективе.
- Всегда говорил, что искусству без науки не прожить, - походя ввертывает Мате. - Но давайте все же не отвлекаться! Следующая разновидность - проектирование параллельное. В этом случае лучи проводятся не из одного центра, а из каждой точки проектируемого контура.
Фило тычет в чертеж пухлым, по-детски оттопыренным пальцем.
- А почему ваши лучи косые?
- Так мне хочется! Имею полное право проводить лучи в любом направлении, с тем условием, чтобы все они были параллельны друг другу. Если же я проведу их не наклонно, а перпендикулярно к плоскости проекций, - это уже будет проекция ортогональная. Самая, пожалуй, необходимая из всех, потому что именно она используется в начертательной геометрии.
Фило понимающе кивает. Начерталка! У его соседа-студента от одного этого слова нервный тик делается.
Мате признает, что предмет и в самом деле свирепый. Но, увы, без него, так же, впрочем, как и без сопромата, нет настоящего инженера-конструктора!
- Наивосхитительнейший мсье Мате, - жалобно взмаливается бес, делая еще одну отчаянную попытку вернуть расположение разобиженного математика, - не могли бы вы познакомить меня хоть с одной из работ Дезарга? Я так давно об этом мечтаю!
Два великих 'Д'
- Хм... - Мате с досадой отмечает, что злость его на Асмодея испаряется с катастрофической быстротой. - Как-нибудь в другой раз. Впрочем, если вам так уж хочется... - Он решительно хлопает себя по колену. - Ну да ладно, хватит дуться! Вот вам одна, зато чрезвычайно важная, теорема проективной геометрии. Она так и называется: теорема Дезарга.
Два великих 'Д'
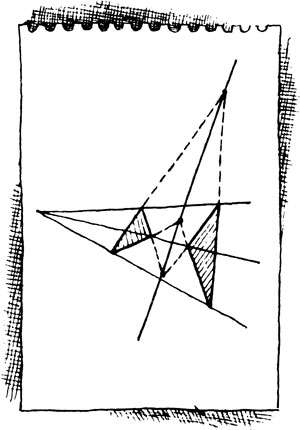
Он вычерчивает небольшой треугольник, поясняя, что размеры его сторон в данном случае никакого значения не имеют, ставит где-то слева от него точку и проводит из нее три луча так, что каждый из них проходит через одну из вершин треугольника.
- Центральное проектирование, - глубокомысленно определяет Фило.
- Не совсем так, - морщится Мате. - Вернее даже, совсем не так. Ну да сейчас не в том дело... Строим второй треугольник, тоже с тем расчетом, чтобы каждая из трех его вершин оказалась на одном из трех лучей... Незачем говорить, что таких треугольников можно нагородить сколько угодно. А теперь продолжим в одном и в другом треугольнике те стороны, концы которых лежат на общих лучах, до тех пор, пока они не пересекутся. Точки пересечения обозначим пожирнее и увидим, что все они, эти точки, лежат на одной прямой.
Бес изучает чертеж с неподдельным интересом. Так вот она какая, теорема Дезарга! Очень, очень оригинальна... Теперь бы еще разузнать доказательство - и более счастливого черта не сыщешь во всей преисподней!
По правде говоря, тонкий намек его ни к чему, ибо если сам Асмодей жаждет получить объяснения, то Мате просто умирает от желания дать их. Он уже готовится произнести свое излюбленное "итак", но Фило, который как раз в это время на собственном опыте постигает справедливость пословицы "Голод не тетка", зажимает ему рот ладонью.
- Только не теперь! Вы что, хотите, чтобы я съел себя самого?
Вид у него такой воинственный, что Мате нехотя уступает. В конце концов, для доказательств есть у них домашние итоги. Хотя кое-что надо бы подытожить сейчас: они так увлеклись разговором о двух великих "Д", что совсем забыли о великом "П"!
- О Паскале, что ли? - нетерпеливо расшифровывает Фило. - По-моему, тут и так все ясно! Паскаль - ученик и последователь Дезарга.
Но Мате столь куцый вывод явно не устраивает. Последователи, говорит он, бывают разные. Одни рабски повторяют кем-то найденное, другие - творят заново. В данном случае не то главное, что Паскаль, совсем еще, в сущности, мальчик, в совершенстве овладел сложными приемами Дезарга, а то, что он проявил себя зрелым ученым и обогатил метод учителя. Доказательство тому - "Опыт о конических сечениях", юношеский трактат Паскаля. Он невелик - всего 53 строки. Но изложенные в нем теоремы заставили говорить о себе всю ученую Францию! А одна из них - теорема о шестивершиннике (Дезарг назвал ее "великой паскалевой") - навсегда останется в числе главных теорем проективной геометрии.
- Ага! - азартно уличает Фило. - Вот когда вы раскрыли свои карты! Вы, как и Паскаль, тоже сторонник Дезарга. И не вздумайте отпираться! Очень уж горячо вы о нем говорите.
Колючие глазки Мате разглядывают его с подчеркнутым любопытством. Ну и упрямец! Умри, а скажи ему, кто лучше: Декарт или Дезарг. Но что же делать, если оба хороши!
- Вот и прекрасно! - весьма непоследовательно сдается Фило. - А теперь - завтракать, завтракать и в третий раз завтракать!
Он достает откуда-то из-за пазухи нечто завернутое в белоснежную салфетку и жестом первоклассного официанта отгибает туго накрахмаленные уголки.
- Прошу!
Мате подозрительно косится на содержимое свертка. Неужто паштет Генриха Второго? В таком случае, завтрак не для него. О, он отнюдь не привередлив, скорее напротив. Но питаться паштетом двадцатилетней давности?! Слуга покорный!
Асмодей, впрочем, убеждает его, что межвременные перелеты на свежести продуктов не отражаются, и мгновение спустя воздушное трио уплетает так, что за ушами трещит.
- Эх, хорош был завтрак! - говорит Фило, мечтательно орудуя зубочисткой. - К нему бы еще подходящий десерт...
- Могу предложить мою собственную теорему, - невозмутимо отзывается Мате.
Два великих 'Д'
Фило довольно ядовито замечает, что имел в виду десерт, а не диссертацию. Но Мате говорит, что диссертация куда полезнее: от нее по крайней мере не толстеют.
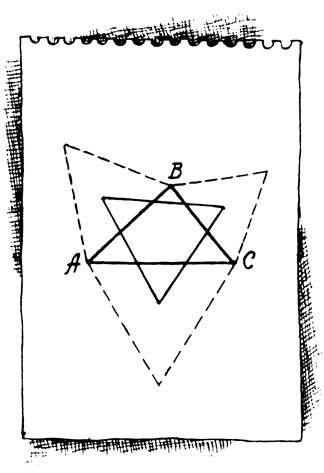
Он вычерчивает треугольник ("Совершенно произвольный, заметьте!"). На каждой из его сторон, снаружи ("А можно и внутри, значения не имеет..."), строит еще по одному треугольнику - теперь уже равностороннему. Отмечает карандашом центры тяжести во всех трех, заново построенных, и соединяет их прямыми.
- Вот и все! Обратите, пожалуйста, внимание на то, что последний, пятый треугольник получился тоже равносторонний.
- Случайность? - предполагает Фило.
- Закономерность.
- Ну, это еще надо доказать...
- Вот и доказывайте. Кто ж вам мешает?
- Один?! - пугается Фило. - Без вашей помощи?
- А то как же! Само собой, тут вам не обойтись без наводящих сведений. Кое-что, так и быть, подброшу. Прежде всего необходимо использовать теорему Пифагора, далее - уметь находить центр тяжести треугольника и вычислять расстояние между двумя точками по их координатам. И, наконец, знать координаты вершин исходного треугольника.
- Милль реконнессанс... тысяча благодарностей, мсье! - рассыпается бес. - Теорема Пифагора - это как раз по мне. Несколько хуже, правда, обстоит дело с расстоянием между двумя точками. Это уж, по-моему, из аналитической геометрии.
- Сущие пустяки! - отмахивается Мате. - Обозначьте координаты точек: Х1, Y1 и Х2, Y2. А расстояние между ними - буквой d. Тогда, опять-таки по теореме Пифагора,
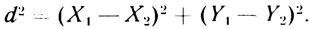
- Учту. Непременно учту, - подобострастно склоняет голову Асмодей. - Не будет ли еще каких-нибудь ценных указаний? ЦУ, как говорят москвичи двадцатого века...
- Хорошо, что напомнили! Советую рассмотреть два частных случая, когда первоначальный треугольник вырождается, а проще сказать - превращается в отрезок прямой. Это происходит либо тогда, когда одна из сторон "треугольника" равна сумме двух других, либо когда она равна нулю. Ну вот, на сей раз действительно все!
Черт стремительно вскакивает и отвешивает один из самых своих изысканных, самых глубоких поклонов.
- Примите уверения в моей бесконечной признательности, наивосхитительнейший мсье Мате! Поверьте, это был лучший десерт в моей жизни. Во всяком случае за последнее тысячелетие...
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'