3. Применения теории Уитни

Поскольку гладкие отображения встречаются повсеместно, повсюду должны встречаться и их особенности. А поскольку теория Уитни дает значительную информацию об особенностях отображений общего положения, можно попытаться использовать эту информацию для изучения большого количества разнообразных явлений и процессов во всех областях естествознания. В этой простой идее и состоит вся сущность теории катастроф.

В случае, когда отображение, о котором идет речь, достаточно хорошо известно, имеется в виду более или менее прямое применение математической теории особенностей к различным явлениям природы. Такое применение действительно приводит к полезным результатам, например в теории упругости и в геометрической оптике (теория особенностей каустик и волновых фронтов, о которых мы еще будем говорить дальше).

Однако в большинстве работ по теории катастроф речь идет о куда более спорной ситуации, когда не только неизвестно изучаемое отображение, но и само его существование весьма проблематично.

Приложения теории особенностей в этих ситуациях носят характер спекуляций: чтобы дать о них представление, мы воспроизводим принадлежащий английскому математику К. Зиману пример спекулятивного применения теории Уитни к исследованию деятельности творческой личности.

Будем характеризовать творческую личность (например, ученого) тремя параметрами, называемыми "техника", "увлеченность", "достижения". По-видимому, между этими параметрами должна быть зависимость. Тем самым возникает поверхность в трехмерном пространстве с координатами (Т, У, Д).

Спроектируем эту поверхность на плоскость (Т, У) вдоль оси Д. Для поверхности общего положения особенности - складки и сборки (по теореме Уитни). Утверждается, что сборка, расположенная так, как это изображено на рис. 6, удовлетворительно описывает наблюдаемые явления.

Действительно, посмотрим, как в этих предположениях будут меняться достижения ученого в зависимости от его техники и увлеченности. Если увлеченность невелика, то достижения монотонно и довольно медленно растут с техникой. Если увлеченность достаточно велика, то наступают качественно новые явления. В этом случае достижения с ростом техники могут расти скачком (такой скачок будет, например, если техника и увлеченность меняются вдоль кривой 1 на рис. 6 в точке 2). Область высоких достижений, в которую мы при этом попадаем, обозначена на рис. 6 словом "гении".

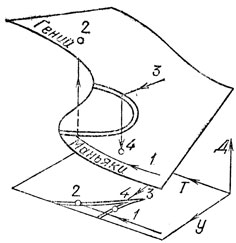
Рис. 6. Модель 'ученый' в пространстве 'техника - увлеченность - достижения'

С другой стороны, рост увлеченности, не подкрепленный соответствующим ростом техники, приводит к катастрофе (на кривой 3 в точке 4, рис. 6), при которой достижения скачком падают, и мы попадаем в область, обозначенную на рис. 6 словом "маньяки". Поучительно, что скачки из состояния "гений" в состояние "маньяк" и обратно происходят на разных линиях, так что при достаточно большой увлеченности гений и маньяк могут иметь равные увлеченности и техники, различаясь лишь достижениями (и предысторией).

Недостатки описанной модели и множества аналогичных ей спекуляций в теории катастроф слишком очевидны, чтобы о них говорить подробно. Отмечу только, что работы по теории катастроф отличает резкое, катастрофическое снижение уровня требований к строгости, а также к новизне публикуемых результатов. Если первое можно понять как реакцию на традиционный в математике поток строгих, но малоинтересных, эпигонских работ, то небрежное отношение катастрофистов к своим предшественникам (которым и принадлежит большинство конкретных результатов) вряд ли можно оправдать. Причина в обоих случаях скорее социальная, чем научная^*.

^*("Я так думаю, голубушка, что декадентство это самое не что иное, как просто к купечеству подход". - В. М. Дорошевич. Рассказы и очерки (М., 1966. С. 295).)