
Беседа 9. Классификация математических понятий
Среди умений, которым учит математика и которым всем вам нужно учиться, большое значение имеет умение классифицировать понятия.
Дело в том, что математика, как и многие другие науки, изучает не единичные предметы или явления, а массовые. Так, когда вы изучаете треугольники, то изучаете свойства любых треугольников, а их бесконечное множество. Вообще объем любого математического понятия, как правило, бесконечен.
Для того чтобы различать объекты математических понятий, изучить их свойства, обычно эти понятия делят на виды, классы. Ведь, кроме общих свойств, любое математическое понятие обладает еще многими важными свойствами, присущими не всем объектам этого понятия, а лишь объектам некоторого вида. Так, прямоугольные треугольники, кроме общих свойств любых треугольников, обладают многими свойствами, весьма важными для практики, например теоремой Пифагора, соотношениями между углами и сторонами и т. д.
В процессе многовекового изучения математических понятий, в процессе их многочисленных применений в жизни, в других науках из их объема были выделены какие-то особые виды, имеющие наиболее интересные свойства, которые чаще всего встречаются и применяются в практике. Так, различных четырехугольников существует бесконечно много, но в практике, в технике наибольшее применение имеют лишь определенные их виды: квадраты, прямоугольники, параллелограммы, ромбы, трапеции.
Деление объема некоторого понятия на части и есть классификация этого понятия. Более точно под классификацией понимают распределение объектов какого-либо понятия на взаимосвязанные классы (виды, типы) по наиболее существенным признакам (свойствам). Признак (свойство), по которому про-изводится классификация (деление) понятия на виды (классы), называется основанием классификации.
Правильно построенная классификация понятия отражает наиболее существенные свойства и связи между объектами понятия, помогает лучше ориентироваться в множестве этих объектов, дает возможность устанавливать такие свойства этих объектов, которые наиболее важны для применения этого понятия в других науках и житейской практике.
Классификация понятия производится по одному или нескольким наиболее существенным основаниям.
Так, треугольники можно классифицировать по величине углов. Получаем такие виды: остроугольные (все углы острые), прямоугольные (один угол прямой, остальные острые), тупо-угольные (один угол тупой, остальные острые). Если же за основание деления треугольников принять соотношения между сторонами, то получаем такие виды: разносторонние, равнобедренные и правильные (равносторонние).
Сложнее, когда приходится классифицировать понятие по нескольким основаниям. Так, если выпуклые четырехугольники классифицировать по параллельности сторон, то по существу нам нужно разделить все выпуклые четырехугольники одновременно по двум признакам: 1) одна пара противоположных сторон параллельна или нет; 2) вторая пара противоположных сторон параллельна или нет. Получаем в результате три вида выпуклых четырехугольников: 1) четырехугольники с не параллельными сторонами; 2) четырехугольники с одной парой параллельных сторон - трапеции; 3) четырехугольники с двумя парами параллельных сторон - параллелограммы.
Весьма часто производят классификацию понятия поэтапно: сначала по одному основанию, затем некоторые виды делят на подвиды по другому основанию и т. д. Примером может служить классификация четырехугольников. На первом этапе их делят по признаку выпуклости. Затем выпуклые четырехугольники делят по признаку параллельности противоположных, сторон. В свою очередь параллелограммы делят по признаку наличия прямых углов и т. д.
При проведении классификации необходимо соблюдать определенные правила. Укажем главные из них.
- В качестве основания классификации можно брать лишь общий признак всех объектов данного понятия. Так, например, нельзя в качестве основания классификации алгебраических выражений брать признак расположения членов по степеням какой-то переменной. Этот признак не является общим для всех алгебраических выражений, например для дробных выражений или одночленов он не имеет смысла. Этим признаком обладают лишь многочлены, поэтому многочлены можно классифицировать по наивысшей степени главной переменной.
- Основанием для классификации надо брать существенные свойства (признаки) понятий. Рассмотрим опять понятие алгебраического выражения. Одним из свойств этого понятия является то, что переменные, входящие в алгебраическое выражение, обозначаются какими-то буквами. Это свойство является общим, но не является существенным, ибо от того, какой буквой обозначена та или иная переменная, характер выражения не зависит. Так, алгебраические выражения х+у и а+b - это по сути дела одно и то же выражение. Поэтому классифицировать выражения по признаку обозначения переменных буквами не следует. Другое дело, если за основание классификации алгебраических выражений взять признак вида действий, с помощью которых переменные соединены, т. е. действия, которые совершаются над переменными. Этот общий признак весьма существенный, и классификация по этому признаку будет правильной и полезной.
- На каждом этапе классификации можно применять лишь одно какое-то основание. Нельзя одновременно классифицировать понятие по двум различным признакам. Например, нельзя классифицировать треугольники сразу и по величине и по соотношению между сторонами, ибо в результате мы получим классы треугольников, которые имеют общие элементы (например, остроугольные и равнобедренные или тупоугольные и равнобедренные и т. д.). Здесь нарушено следующее требование к классификации: в результате классификации на каждом этапе получаемые классы (виды) не должны пересекаться.
- В то же время классификация по какому-либо основанию должна быть исчерпывающей и каждый объект понятия должен попасть в результате классификации в один и только один класс.
Поэтому разделение всех целых чисел на положительные и отрицательные неверно, ибо целое число нуль при этом не попало ни в один из классов. Надо говорить так: целые числа делятся на три класса - положительные, отрицательные и число нуль.
Часто при классификации понятий явно выделяются лишь некоторые классы, а остальные только подразумеваются. Так, например, при изучении алгебраических выражений обычно выделяют лишь такие их виды: одночлены, многочлены, дробные выражения, иррациональные. Но эти виды не исчерпывают всех видов алгебраических выражений, поэтому такая классификация является неполной.
Полная правильная классификация алгебраических выражений может быть произведена следующим образом.
На первой ступени классификации алгебраических выражений они делятся на два класса: рациональные и нерациональные. На второй ступени рациональные выражения делятся на целые и дробные. На третьей ступени целые выражения делятся на одночлены, многочлены и сложные целые выражения.
Эту классификацию можно представить в виде следующей
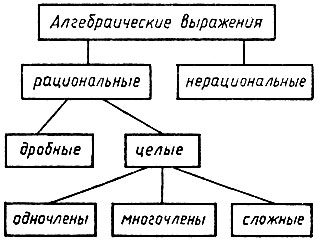
Задание 7
7.1. Почему нельзя классифицировать рациональные числа по их четности?
7.2. Установите, правильно ли произведено деление понятия:
а) Величины могут быть равными и неравными.
б) Функции бывают возрастающие и убывающие.
в) Равнобедренные треугольники могут быть остроугольными, прямоугольными и тупоугольными.
г) Прямоугольники бывают квадраты и ромбы.
7.3. Произведите деление понятия "геометрическая фигура" по свойству занимать часть плоскости и приведите примеры каждого вида.
7.4. Постройте возможные схемы классификации рациональных чисел.
7.5. Постройте схему классификации следующих понятий:
а) четырехугольник;
б) два угла.
7.6. Проведите классификацию следующих понятий:
а) треугольник и окружность;
б) углы в окружности;
в) две окружности;
г) прямая и окружность;
д) квадратные уравнения;
е) система двух уравнений первой степени с двумя неизвестными.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'