Беседа 4. Математические объекты

Чтобы ответить на вопрос, чему учиться в математике, надо разобраться в том, что она - математика - собой представляет, в чем ее особенности, что и как она изучает и из каких элементов (объектов) она состоит. Конечно, все эти вопросы очень сложные, и мы подробно в них разобраться не сумеем, но получить хотя бы некоторое представление обо всем этом нам необходимо, ибо иначе просто невозможно решить, чему же учиться в математике.

Математика, как и другие науки, изучает окружающий нас мир, природные и общественные явления, но изучает лишь особые стороны этих явлений.

Представьте себе, что нужно рассчитать, сколько надо купить краски, чтобы покрасить потолок комнаты, если известно, что на окраску 1 м² уходит 120 г краски, или сколько нужно купить кафельных плиток для облицовки стены, если известно, что плитка имеет форму квадрата со стороной 15 см. Во всех этих случаях совершенно безразлично, какого цвета этот потолок или стена, из какого материала они построены и т. д. Важно лишь знать их форму и размеры. В этом случае говорят, что мы отвлекаемся (абстрагируемся) от всех свойств рассматриваемого предмета и выделяем лишь его форму и размер. В результате такого абстрагирования получаем математический объект - геометрическую фигуру.

В других случаях, кроме формы и размера, учитывают еще взаимное расположение частей фигуры.

Такие математические объекты, как числа, образуются путем выделения при рассмотрении различных совокупностей (множеств) однородных предметов таких общих свойств, как количество предметов в совокупности или их порядок следования, абстрагируясь от всех других свойств этих предметов (их неодинаковости, материала, цвета, величины и т. д.).

Вообще любые математические объекты - это результат выделения из предметов и явлений окружающего мира особых количественных и пространственных свойств и отношений и абстрагирования от всех других свойств. Следовательно, математические объекты реально не существуют, нет в окружающем нас мире геометрических точек, фигур, чисел и т. д. Все они созданы человеческим умом в процессе исторического развития людей и существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык. Поэтому говорят, что математические объекты - это идеальные объекты, отражающие (описывающие) реальные объекты.

Обратите внимание еще на одну особенность математических объектов. При их образовании мы не только отвлекаемся от многих свойств соответствующих предметов, но и приписываем им такие свойства, которыми никакие реальные предметы не обладают. Так, например, образуя такой математический объект, как прямая линия, мы в соответствующих предметах (край линейки, стола, луч света, нить и т. д.) не только абстрагируемся от всех их свойств, кроме свойства протяженности, но и приписываем такое свойство, как неограниченная протяженность в обоих направлениях, хотя никакой из указанных реальных предметов таким свойством не обладает. Точно так же никакая совокупность реальных предметов не является бесконечной, а вот множество натуральных чисел бесконечное, или никакой предмет не является бесконечно раздробленным, а вот число - размер этого предмета, мы считаем бесконечно раздробляемым, т. е. число можно делить на какое угодно большое число частей, и т. д.

Итак, математика изучает особые идеальные математические объекты, которые образуются путем сложной мыслительной деятельности людей в процессе познания количественных свойств и отношений, а также пространственных свойств и форм предметов и явлений окружающего мира.

Поэтому первое, чему надо учиться в математике,- это умению в процессе изучения каких-то предметов или явлений для решения задач по определению количественной стороны или пространственных соотношений этих предметов или явлений образовывать, создавать математические объекты. Рассмотрим в качестве примера такую задачу.

Задача.Для того чтобы укрепить железную дымовую трубу, было решено на высоте 20 м от ее основания прикрепить растяжки из стального каната, которые закрепить к четырем бетонным тумбам, находящимся на расстоянии 15 м от основания трубы. Сколько каната для этого потребуется? (Рис. 2.)

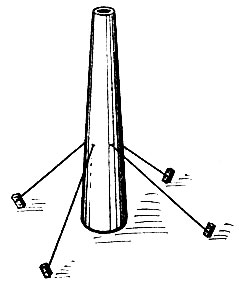
Рис. 2

Решение. Примем дымовую трубу за отрезок прямой, перпендикулярной поверхности земли, а бетонные тумбы - за точки на поверхности земли. Так как для нахождения длины всего потребного каната для четырех растяжек достаточно найти длину одной из них, то получаем такую геометрическую задачу: "Найти длину гипотенузы прямоугольного треугольника, катеты которого равны 20 и 15 метрам".

В этом примере реальные объекты - труба, бетонные тумбы, канаты - мы заменили математическими объектами - отрезками прямых, точками, для чего пришлось абстрагироваться (отвлечься, не учитывать) от таких особенностей этих реальных объектов, как конусность и толщина трубы, размеры тумб, высота их над поверхностью земли и т. д. Иными словами, реальное явление, описанное в приведенной задаче, мы заменили идеализированным явлением - геометрической задачей, а поэтому наше решение является приближенным. Однако точность здесь вполне достаточная для практики (ошибка может быть в пределах нескольких сантиметров).

Вообще надо помнить, что математическое решение любой практической задачи всегда является приближенным.

Для того чтобы закрепить полученные знания и проверить себя, как вы их усвоили, выполните следующее задание.

2.1. Какие геометрические фигуры выступают в качестве идеальных образов (моделей) реальных предметов в следующих практических задачах:

а)Найти площадь пятикопеечной монеты.

б) Найти длину обруча.

в) Найти площадь комнаты.

От каких свойств реальных предметов мы при этом абстрагируемся, а какие учитываем?

2.2. За билетами в театр стоит очередь. Какие математические объекты характеризуют положение (место) каждого человека в этой очереди? Какие практические задачи можно решить с помощью этих математических объектов?

2.3. Велосипедист выехал из города А в 9 ч утра и прибыл в город В, отстоящий от А на расстоянии 60 км, в 12 ч дня. Отдохнув в В 2 ч, он поехал дальше в город С, отстоящий от В на 72 км, и прибыл туда в 6 ч вечера.

Как можно наиболее просто и наглядно математически описать событие поездки велосипедиста из А в С? Какие практические задачи можно решить, имея это математическое описание? Какие математические объекты при этом использованы?