3. Функция Эйлера φ(n). Еще раз о теореме Ферма

Говорят, что два целых числа а и b - взаимно простые, если их общий наибольший делитель равен 1:

(а, b) = 1.

Например, числа 24 и 35 взаимно простые, но числа 12 и 18 не взаимно простые.

Если а и b - взаимно простые, то можно подобрать такие целые числа k и l, что

Это следует из свойства (а, b), отмеченного на стр. 70.

Упражнение. Докажите теорему: если произведение ab делится на r, причем r и а - взаимно простые, то b делится на r. (Указание. Если r и а - взаимно простые, то можно найти такие целые числа k и l, что

Затем умножьте обе части равенства на b.) Эта теорема обобщает лемму со стр. 71, так как простое число р в том и только в том случае является взаимно простым с а, если а не делится на р.

Пусть n - произвольное целое положительное число; обозначим через φ(n) число таких целых чисел в пределах от 1 до n, которые являются взаимно простыми с числом n. Выражение φ (n), впервые введенное Эйлером, представляет собой очень важную теоретико-числовую функцию. Легко подсчитать значения φ (n) для нескольких первых значений n:

и т. д.

Заметим, что φ (р) = р - 1, если р - простое число; в самом деле, у числа р нет делителей, кроме 1 и р, и потому все числа 1,2,..., р-1 являются взаимно простыми с р. Если n - составное, причем его разложение на простые множители имеет вид

где числа р обозначают различные простые множители, причем каждое из них возводится в некоторую степень, то тогда

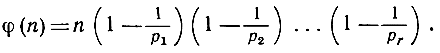
Например, из разложения 12 = 2²*3 следует

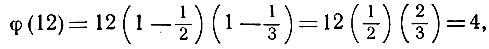
что легко проверить непосредственно. Доказательство приведенной теоремы совершенно элементарно, но мы его не приводим.

Упражнение. Пользуясь функцией Эйлера φ(n), обобщить теорему Ферма, приведенную на стр. 61. Обобщенная теорема формулируется следующим образом: если n - целое число и а - взаимно простое с n, то

а^φ(n) ≡ 1 (mod n).