2. Применение в биологических исследованиях электронных вычислительных машин

1. Чем может помочь биологу вычислительная машина

Характерная черта современных биологических, в частности, физиологических исследований - это обилие экспериментальных данных. Нередко исследователь буквально тонет в этих данных, тратя дни и недели на обработку результатов, полученных за сравнительно непродолжительный опыт. Естественно, что экспериментатор с надеждой обращает свой взор к быстродействующим вычислительным машинам, надеясь получить помощь отсюда.

Для этих надежд есть достаточные основания. Однако для того чтобы эти надежды оправдались, важно четко представлять себе, что вычислительная машина «умеет» и чего она «не умеет». Неправильное представление о возможной роли вычислительной техники в тех или иных исследованиях приводит иной раз вот к каким ситуациям. Приходит биолог к математику (желательно, такому, который располагает вычислительной машиной) и говорит, что у него накопилась масса экспериментального материала, который надо было бы «математически обработать».

- Хорошо, а как именно вы хотите его обрабатывать?

- Ну, это уж ваше дело, на то вы и математики.

- А в чем состоит ваша задача, на какой вопрос вы хотите получить ответ?

И вот, при дальнейшем разговоре нередко выясняется, что четкой постановки задачи собственно и нет, а есть лишь надежда, что при той или иной обработке экспериментальных данных «выплывут» какие-то связи и закономерности. И в этих случаях приходится объяснять следующее. Да, вычислительные машины могут многое. Они неизмеримо увеличивают наши вычислительные возможности. Они могут хранить и оперативно использовать большие запасы информации. Но вычислительные машины не смогут дать нам никаких заслуживающих внимания результатов, если у нас нет четко поставленной задачи. К вычислительной математике со всей ее современной техникой полностью применимы слова по поводу математики вообще, сказанные Гексли (их часто приводил акад. А. Н. Крылов). Математика, говорил он, подобна мельнице: если в нее насыпать зерно, то получится мука, а если насыпать трухи, то только труха и получится.

Для того чтобы пояснить реальные возможности использования вычислительных машин в биологических исследованиях, скажем несколько слов о самих этих машинах, не входя, конечно, в детали их устройства и эксплуатации.

2. Несколько слов о вычислительной технике

В вычислительной технике сложилось деление машин на специализированные и универсальные. Специализированными называют машины, предназначенные для выполнения какой-то определенной совокупности операций - например, анализа частот, составляющих некоторый колебательный процесс, решения уравнений или систем уравнений определенного вида и т. д. Такие специализированные машины, как правило, не слишком сложны и громоздки, не требуют для своего обслуживания высококвалифицированного инженерного персонала, а потому и достаточно доступны. С другой стороны, в этих машинах уже зафиксирован соответствующий способ обработки информации, и переход на какие-то новые методы или задачи требует и новых машин.

Гораздо более широкими возможностями обладают универсальные вычислительные машины, в первую очередь универсальные цифровые вычислительные машины (УЦВМ). В принципе на такой машине реализуется любой процесс, который может быть представлен как последовательность элементарных логических или математических операций. Мы не будем здесь описывать принципы устройства УЦВМ, а обратим внимание лишь на следующее.

Универсальные вычислительные машины применяются сейчас в самых разных областях - для решения собственно математических задач, в вопросах управления производством, при анализе текста (например, при расшифровке древних письмен) и т. д. Однако для этих разнородных задач используются одни и те же машины, а разнообразие задач, которые машина может решать,- это на самом деле разнообразие тех программ работы, которые такой машине могут быть заданы. В частности, с помощью соответствующих программ на УЦВМ можно реализовать самые различные методы обработки данных биологического эксперимента - как уже существующие, так и те, которые еще будут придуманы.

Современные электронные вычислительные машины работают со скоростью до нескольких миллионов операций в секунду. Поэтому они в состоянии обрабатывать огромное количество самой разнообразной информации, в том числе и биологической. Однако на пути между биологическим экспериментом и цифровой вычислительной машиной стоит одно существенное препятствие, которое можно назвать «отсутствием общего языка». Вот что это значит. Цифровая вычислительная машина способна воспринимать и перерабатывать информацию, записанную в цифровом виде, в определенной системе. (Для подавляющего большинства машин такой системой служит так называемая двоичная система, в которой каждое число представляется некоторой последовательностью нулей и единиц). В то же время те данные, которые получаются непосредственно из физиологического эксперимента, вовсе не выражены в числах. Например, введя микроэлектрод в нервную клетку, мы можем регистрировать изменения электрического потенциала клетки. Однако эта величина - потенциал клетки - не может быть непосредственно введена в вычислительную машину: предварительно ее значения в различные моменты времени должны быть выражены цифрами, так как только цифры представляют собой тот «язык», который «понимает» УЦВМ. Если этот процесс перевода физиологических данных в цифры проделывать вручную, то мы сразу же потеряем все преимущества, связанные с применением быстродействующих вычислительных машин, так как такой перевод будет занимать массу времени. Следовательно, его нужно автоматизировать. Существуют специальные устройства - так называемые аналого-цифровые преобразователи, ? осуществляющие такое преобразование автоматически. Такие устройства позволяют быстро и с достаточной точностью переводить непрерывно меняющиеся величины (скажем, изменения потенциала клетки) в последовательность цифр, которые может воспринимать машина.

3. Обработка данных в ходе эксперимента

Выполнив ту или иную экспериментальную работу, физиолог, конечно, не хочет ждать месяцы для получения результатов обработки данных этого опыта. Конечно, гораздо лучше получить эти результаты, скажем, на следующий день. Однако и это не предел мечтаний. Лучше всего иметь результаты опыта в обработанном виде сразу же, пока опыт еще не закончился. Тогда в зависимости от уже полученных результатов можно как-то изменить или ход опыта или метод обработки, продолжить накопление данных, если они оказываются недостаточно убедительными, и т. д. Если же обработка данных опыта начинается лишь после его окончания, то сам опыт ведется в известной мере «вслепую». Поэтому каждый экспериментатор хочет видеть результаты опыта сразу же, как говорят, в реальном времени, т. е. так, чтобы информация не накапливалась, а обрабатывалась без задержки, по мере ее поступления. В настоящее время такие методы обработки данных физиологического эксперимента вполне реальны и даже получили довольно широкое распространение^*.

^* (Обработка данных непосредственно в ходе самого эксперимента с минимальной задержкой важна, конечно, не только в физиологических исследованиях, но и во многих других областях - при исследовании химических реакций, технологических процессов и т. д., однако рассмотрение всех этих интересных и важных проблем выходит за рамки нашей темы.)

При таком использовании вычислительной техники установка, на которой производится тог или иной физиологический эксперимент (скажем, регистрируется изменение электрической активности отдельной нервной клетки), соединяется через такие необходимые вспомогательные приспособления, как усилители, аналого-цифровой преобразователь и т. п., с УЦВМ. Соответствующим образом усиленные и преобразованные в цифровой код сигналы от изучаемого объекта поступают прямо в вычислительную машину и тут же ею обрабатываются. Для того чтобы экспериментатор мог видеть результаты такой обработки быстрее и отчетливее, эти результаты лучше не печатать в цифровом виде на бумажной ленте (как это обычно делается в вычислительных машинах), а представлять в каком-либо более наглядном виде, например в виде графиков или таблиц на светящемся экране. При тех скоростях, с которыми работают современные вычислительные машины, и при условии, что программа обработки данных не слишком сложна, экспериментатор видит результаты своего эксперимента практически без всякой задержки. Такой метод применения вычислительной техники называется использованием машины «в реальном времени» или «в линии эксперимента». Приведем описание одной конкретной физиологической работы, в которой использование вычислительной машины «в реальном времени» во много раз ускоряет и облегчает работу экспериментатора.

Рис. 1. Запись электрической активности одиночного нейрона (схема)

Изучается реакция одиночного нейрона слухового нерва кошки на звуковые раздражения различной силы, высоты тона и продолжительности. Как спонтанная, так и вызванная активность такого волокна представляет собой последовательность отдельных, очень коротких импульсов - «спайков» (см. рис. 1). Расстояния между соседними спайками (межспайковые интервалы) не постоянны, а в значительной мере случайны. Распределение длин этих интервалов можно охарактеризовать с помощью так называемой гистограммы, т. е. кривой, построенной так, что площадь, заключенная между прямыми t=t₁ и t=t₂ представляет собой относительную долю интервалов, длина которых заключена между t₁ и t₂. Раздражение существенно меняет вид гистограммы (см. рис. 2, а и 2, б), причем для каждого нейрона слухового нерва можно подобрать параметры звукового раздражения так, чтобы это изменение было наибольшим. Построение такого рода гистограмм вручную-долгое и утомительное дело.

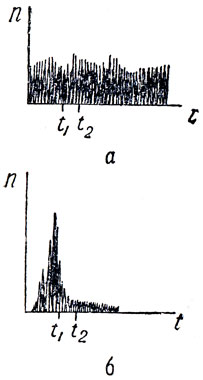
Рис. 2. Гистограмма межспайковых интервалов одиночного нейрона: а – при отсутствии раздражения, б – при звуковом раздражении

Современная вычислительная техника позволяет вести описанный выше эксперимент следующим образом. С микроэлектрода, введенного в нейрон, импульсы подаются на соответствующее аналого-цифровое устройство, переводящее промежутки между соседними импульсами в цифровой код (в двоичной системе счисления). Далее эти данные поступают в вычислительную машину, которая по соответствующей программе строит гистограмму. Эта гистограмма, которая, естественно, меняется по мере накопления материала, водится на светящийся экран так, что экспериментатор ее все время видит. Если экспериментатор хочет зафиксировать построенную гистограмму, то он включает нажатием кнопки связанный с машиной фотоаппарат и получает фотографию этой гистограммы

4. Вычислительная машина - участник эксперимента

Пока что мы говорили только о передаче машине функций обработки экспериментального материала. Однако, располагая в физиологической лаборатории современной вычислительной техникой, естественно попытаться сделать еще один шаг и возложить на УЦВМ не только обязанности по обработке результатов эксперимента, но и некоторые функции самого экспериментатора. Именно машина может в зависимости от уже полученных результатов направлять дальнейший ход эксперимента тем или иным путем, скажем, включать или выключать некоторый стимулятор и т. п. Важно подчеркнуть, что машина способна «принимать решение» или «давать команду» несравненно быстрее, чем это может делать человек, и, следовательно, реагировать на тот или иной результат гораздо оперативнее, чем сам экспериментатор.

Изложенная нами идея активного участия вычислительной машины, как управляющего органа, в биологическом эксперименте уже была с успехом реализована в некоторых лабораториях.

Выше были высказаны некоторые общие соображения о применении вычислительных машин в биологических исследованиях. Сейчас мы кратко опишем несколько конкретных работ такого рода, в которых применение вычислительной техники имело существенное, а иногда и решающее значение. Таких работ сейчас уже достаточно много, поэтому перечислить их было бы невозможно. Мы остановимся лишь на некоторых примерах, выбор которых в значительной мере случаен.

5. Анализ биоэлектрических потенциалов головного мозга

В лаборатории проф. М. Н. Ливанова была проделана следующая работа. С помощью специальной многоканальной системы производится одновременная запись биопотенциалов с большого числа (до 100) участков коры головного мозга и исследуется степень зависимости между данными, полученными с разных точек, например при выработке условного рефлекса (эксперимент проделывается на кроликах). Техника этой работы такова. По каждому из каналов через определенные (достаточно малые) промежутки времени измеряется величина потенциала. Значения этого потенциала, измеренные для двух соседних моментов времени, сравниваются между собой, и пишется знак +, - или 0, в зависимости от того, происходит ли возрастание потенциала, его убывание, или же этот потенциал остается неизменным (в пределах принятой точности измерения). Таким образом, в каждой точке весь процесс изменения биопотенциала представляется в упрощенной форме как последовательность плюсов, минусов и нулей. Эти данные могут быть введены в вычислительную машину, которая подсчитывает коэффициент синхронизации (= процент совпадений) между любыми двумя такими последовательностями. Такая обработка позволила получить интересные данные об электрической активности мозга в процессе формирования условного рефлекса. Общая картина такова: до начала выработки условного рефлекса синхронизация различных участков мозга незначительна; в процессе выработки рефлекса эта синхронизация резко возрастает, а после полной отработки рефлекса снова существенно падает.

Несколько иное исследование было поставлено для биопотенциалов головного мозга человека. При этом с помощью сходной методики, т. е. записи биопотенциалов от отдельных участков коры, было обнаружено, что если человеку предложить мысленно решать некоторую задачу (например, перемножить два двузначных числа), то в процессе ее решения происходит резкое изменение (и увеличение) синхронизации активности различных участков коры больших полушарий.

Хотя в описанных выше экспериментах получаемые данные сильно упрощались и значительная часть информации просто отбрасывалась (в каждой точке учитывалось лишь направление изменения потенциала, но не величина этого изменения), обработка даже таких упрощенных данных вручную представляла бы большие трудности. В первоначальных экспериментах подготовка исходных данных для обработки (сопоставление каждой точке последовательности плюсов, минусов и нулей) производилась вручную, что, конечно, сильно снижало тот выигрыш, который давала автоматизация самой обработки. В дальнейшем эти работы были автоматизированы полностью.

6. Определение первичной структуры белка

Как известно, каждая белковая молекула представляет собой последовательность аминокислот, соединенных друг с другом в цепь. Число различных аминокислот равно 20. Различные белковые молекулы содержат сотни и даже тысячи аминокислот. Точная последовательность аминокислот известна сейчас лишь для немногих белков - инсулина, гемоглобина и некоторых других. Для анализа этих белков был использован следующий метод. С помощью соответствующих химических воздействий белковую молекулу разрывали на части. Затем устанавливали (химическими методами) последовательность аминокислот в этих фрагментах и, наконец, с помощью соответствующего комбинаторного анализа, реализуемого на вычислительной машине, восстанавливали всю последовательность аминокислот в молекуле. Идею этого последнего этапа работы можно пояснить на таком элементарном примере. Допустим, что у нас имеется цепочка, состоящая всего лишь из семи аминокислот, которые мы обозначим буквами А, В, С, D, Е, F и G, и имеется два набора фрагментов - один полный (т. е, составляющий в сумме всю нашу молекулу):

и другой неполный:

Комбинируя эти два набора, легко заметить, что наша молекула должна представлять собой одну из следующих двух последовательностей:

Иначе говоря, отрезок

определяется однозначно, а положение элемента G требует дальнейшего уточнения (скажем, путем получения фрагмента вида FG). В рассмотренном примере анализ возможных комбинаций не представил никакого труда. Однако в случае, когда речь идет о цепочках, содержащих сотни элементов, задача восстановления ее структуры по фрагментам становится весьма сложной и требует применения мощной вычислительной техники. Часто эта задача усложняется тем, что для отдельных фрагментов оказывается известным лишь их состав, но не порядок следования элементов, или же в определении этого порядка могут быть ошибки. Конечно, трудность задачи определения структуры белка заключается не только в сложности соответствующего комбинаторного анализа. Первую и весьма существенную трудность здесь представляет сама экспериментальная биохимическая работа по получению и анализу белковых фрагментов,

7. Изучение нормального и патологического тремора

Вернемся снова к некоторым физиологическим применениям вычислительной техники. Если человек вытянет перед собой руку, то она никогда не будет абсолютно неподвижна: рука совершает непроизвольные мелкие колебания. То же самое имеет место и для всех других элементов нашего двигательного аппарата - в каждом суставе мы не можем сохранить абсолютную неподвижность, а обязательно будут происходить колебания вокруг некоторого среднего положения. Это явление называется тремором. У здорового человека тремор невелик - угловые смещения составляют минуты или доли минут. Однако при различных заболеваниях тремор может резко возрастать. Одно из наиболее типичных заболеваний такого рода - так называемая болезнь Паркинсона, при которой тремор в тяжелых случаях возрастает настолько, что человек теряет работоспособность и возможность передвигаться без посторонней помощи. Более внимательное рассмотрение показывает, что при болезни Паркинсона не только увеличивается амплитуда тремора, но и меняется его частотный состав (спектр): если нормальный тремор представляет собой в основном смесь колебаний низкой (около 1 гц), средней (3-4 гц) и высокой частоты (7-8 гц), то в треморе паркинсоника основная составляющая - колебания с частотой около 5 гц, а другие частоты почти полностью отсутствуют. При болезни Паркинсона в тяжелых случаях применяется хирургическое лечение. Операция - так называемая таламэктомия - состоит в разрушении некоторого определенного участка головного мозга. Это достаточно тяжелая операция в некоторых случаях приносит стойкое улучшение, однако в других случаях положительный эффект (т. е. снижение амплитуды тремора до нормы), наступающий сразу после операции, через 2-3 недели исчезает, и возникает примерно такой же тремор, какой был до операции. Проведенный частотный анализ обнаружил следующий факт: стойкий эффект получался в тех случаях, когда после операции тремор становился нормальным не только по амплитуде, но и по частотному составу. Если же амплитуда тремора падала до нормы, но его спектральный состав оставался характерным для паркинсоника, то эффект операции сравнительно быстро исчезал.

Контроль частотного состава спектра можно вести во время самой операции, следя, таким образом, за ее эффективностью и внося в нее соответствующие коррективы (окажем, увеличивая ту область, которая подвергается разрушению). Представляется весьма интересной следующая гипотеза: может быть, достаточно тщательное исследование тремора больного-паркинсоника перед операцией даст какие-то возможности предсказать заранее эффективность оперативного вмешательства? К сожалению, пока еще нет убедительных данных, которые позволили бы ответить на этот вопрос положительно.

Исследование тремора здорового человека также представляет определенный интерес. Так, например, оказалось, что если человеку дать определенную задачу, скажем, удерживать острие карандаша против определенной точки, то тремор имеет несколько иной характер, чем если рука просто находится в покое,- в первом случае высокочастотная компонента заметно больше, чем во втором. Это дает основание считать, что изучение тремора может дать ряд сведений о работе двигательного аппарата человека при выполнении различных задач, требующих точной координации, например при стрельбе.

Для работы по изучению тремора были использованы датчики, превращающие механические отклонения от некоторого среднего положения в электрические, и аналого-цифровой преобразователь, переводящий изменения электрического потенциала в цифровой код. Проведение последующих расчетов (корреляционный и спектральный анализы) сравнительно не сложно. Вместе с тем такая обработка данных позволяет значительно точнее оценить возникающую картину, чем это может сделать визуально самый опытный экспериментатор, рассматривая запись тремора на осциллографе. Важно, что при этом мы не только устанавливаем качественные различия в треморе, но и вычисляем его количественные характеристики.

8. Изучение типов спонтанной и вызванной активности нервных клеток

Нервные клетки, входящие в состав тех или иных структур, образующих центральную нервную систему, могут сильно отличаться друг от друга по своим размерам, строению синаптических связей с другими клетками, количеству и форме ответвлений (дендритов) и т. д. Примером структуры, в пределах которой имеются существенно различные между собой типы клеток, может служить кора мозжечка. Она состоит из так называемых клеток Пуркинье, имеющих сравнительно большие размеры и сложную систему дендритов, мелких зернистых клеток и т. д. Хотя различия в строении этих клеток достаточно отчетливы, функции отдельных типов клеток далеко не ясны. Поэтому представляется интересным изучить возможные для этих клеток типы активности как спонтанной (т. е. самопроизвольной), так и вызванной внешними воздействиями, скажем, раздражением определенного участка тела, и выяснить, отличаются ли клетки с разной структурой и по своим функциям или нет.

Такого типа работы проводятся как в Москве, так и в ряде зарубежных лабораторий. Выполнение подобных исследований требует обработки весьма большого экспериментального материала - в первую очередь составления гистограмм для распределении межспайковых интервалов, т. е. примерно такой же техники, как и упоминавшееся выше изучение реакций отдельных нейронов слухового нерва на акустические раздражения. В последнее время здесь был получен ряд результатов, обнаруживших у различных типов клеток определенные, характерные для них особенности функциональной активности.

9. Математический анализ электрокардиограмм

Приведем еще один пример, на этот раз относящийся к использованию вычислительной техники в целях медицинской диагностики. За последние десятилетия в диагностике различных сердечных заболеваний (инфаркт, стенокардия и т. д.) весьма важную роль стал играть анализ кардиограмм, т. е. кривых, характеризующих электрическую активность сердца. Схематический вид нормальной электрокардиограммы изображен на рис. 3. Сущность процессов, отражаемых кардиограммой, состоит в следующем. Ритмические сокращения работающего сердца связаны с распространением по его объему волны электрического возбуждения. Поэтому сердце создает вокруг себя периодически меняющееся электрическое поле. Кардиограмма и представляет собой запись изменения этого поля. Практически это делается так. Прикладывая электроды к определенным точкам на теле человека, мы записываем соответствующие проекции вектора, характеризующего электрическое поле сердца. Для того чтобы получить более полную информацию об этом поле в целом, делается запись в нескольких точках или, как говорят медики, берется несколько «отведений». Обычно в медицинской практике берется 12 отведений.

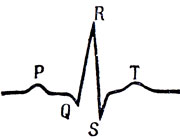
Рис. 3 Схематическое изображение электрокардиограммы (один цикл работы сердца).P,Q,R,S,T ? обозначение «зубцов» (характерных точек) электрокардиограммы

Различные отклонения вида кардиограммы от нормы позволяют врачу-кардиологу судить о тех или иных сердечных заболеваниях, например о наличии инфаркта и его локализации в сердечной мышце. В принципе это выглядит просто, но на самом деле все гораздо сложнее. Прежде всего само понятие «нормальной» кардиограммы достаточно неопределенно. Вид кардиограммы зависит от мелких различий в расположений сердца у разных людей и от многих других факторов, вовсе не связанных с наличием какого-либо заболевания. Поэтому кардиограмма используется для диагностических целей обязательно в сочетании с другими признаками (наличие болей в области сердца, сдвиги в составе крови и т. д.) и во всяком случае требует от человека, делающего по кардиограмме те или иные заключения, высокой квалификации и большого опыта.

Хотя кардиограмма не может служить единственным основанием для тех или иных медицинских заключений, содержащаяся в ней информация о состоянии сердечной мышцы достаточно велика. Особенно важно то, что те или иные изменения в кардиограмме могут быть предвестниками заболеваний сердца (скажем, того же инфаркта), т. е. служить для целей профилактики. Поэтому систематическое кардиографическое обследование широких слоев населения, особенно в среднем и пожилом возрасте, представляет важную задачу. Но нельзя же безгранично увеличивать необходимые для этого медицинские штаты. Естественно, возникает стремление автоматизировать обработку кардиограмм, переложив эту задачу на быстродействующую вычислительную технику. Задача анализа кардиограмм с помощью универсальных вычислительных машин интересна и с теоретической точки зрения, поскольку здесь возникают достаточно сложные математические вопросы.

В решении этой задачи возможны различные подходы. Медицинская практика установила ряд параметров в кардиограмме, существенных для диагностики. К ним относятся: соотношения между высотами зубцов, расстояния между зубцами и т. д. Существуют машинные программы, определяющие эти параметры. Однако определение этих параметров - вовсе не самоцель. Самое важное - по найденным значениям этих параметров поставить диагноз. Поэтому возможны два варианта использования УЦВМ в кардиографии. Во-первых, можно ограничить задачу машины тем, чтобы она находила и представляла в удобном для клинициста виде значения параметров, нужных для постановки диагноза, а само установление диагноза по этим данным считать делом врача. При этом за машиной остаются такие вспомогательные, но важные функции, как, например, выявление ошибочных или искаженных данных, отсеивание случайных внешних помех и т. д.

Другой подход состоит в том, чтобы, введя в машину данные о том, как те или иные отклонения кардиограммы от нормы связаны с различными сердечными заболеваниями, возложить на машину и саму постановку диагноза. Решение такой задачи представляется, конечно, весьма нелегким делом, однако здесь уже намечены некоторые подходы и получены первые обнадеживающие результаты. Не имея возможности излагать здесь детали, ограничимся лишь следующим.

Предположим, что нам нужно научить кого-либо различать фигуры разных типов, скажем, эллипсы, треугольники и квадраты. Можно этого добиться следующим образом. Сперва возьмем какой-то материал для обучения, т. е. некоторое количество образцов каждого из трех типов, будем их показывать по очереди и каждый раз говорить, что это такое. Ясно, что вскоре обучаемый сможет различать любые квадраты, треугольники и эллипсы. Едва ли каждое лицо, умеющее отличать квадрат от эллипса, может точно сформулировать рецепт, по которому он это делает, но, по-видимому, процесс состоит в том, что человек фиксирует у себя в памяти (может быть, бессознательно) некоторые характерные признаки показываемых ему фигур (скажем, у эллипса отсутствуют прямолинейные участки, квадрат составлен из четырех прямолинейных отрезков и т. д.) и затем пользуется этими признаками.

Такое обучение путем предъявления образцов и отбора на этих образцах характерных признаков возможно не только для человека, но и для вычислительной машины. Эта идея может быть положена в основу классификации кардиограмм и установления диагноза, хотя, конечно, задача о классификации кардиограмм несравненно сложнее, чем задача различения разных геометрических фигур. К вопросу об обучении машины распознаванию образов мы еще вернемся.