
2. Группы
Прежде чем дать определение группы, рассмотрим один важный пример.
Будем исходить из понятия взаимно однозначного отображения множества на себя. В случае конечного множества такое отображение называют обычно подстановкой. Пусть множество М состоит из чисел 1, 2, 3: М = {1, 2, 3}. Чтобы задать какую-либо подстановку множества М, достаточно указать для каждого из чисел 1, 2, 3 то число, в которое оно отображается этой подстановкой. Удобнее всего сделать это, использовав таблицу из двух строк, - в первой строке выписываются (в любом порядке) числа 1, 2, 3, а во второй под каждым из них пишется соответствующее ему при данной подстановке число. Скажем, обе таблицы
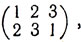
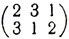
задают одну и ту же подстановку: число 1 переходит в число 2, 2 - в 3, 3 - в 1. Нетрудно указать все различные подстановки множества М; их будет шесть:
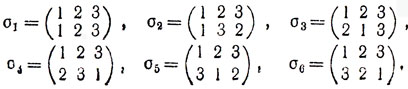
Определим теперь на множестве S = {σ1, σ2, ..., σ6} всех подстановок операцию умножения (или композицию) подстановок. Именно, произведением подстановок σi и σj будем называть подстановку σk, получающуюся в результате последовательного выполнения сначала подстановки σi, а затем σj (записывается: σiσj = σk). Например,
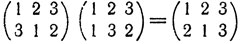
(первая подстановка переводит число 1 в число 3, после чего вторая подстановка переводит число 2 в число 3, так что в результате последовательного выполнения подстановок число 1 перейдет в число 2 и т, д.). Читатель может проверить, что
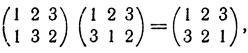
и тем самым убедиться, что произведение двух подстановок зависит, вообще говоря, от порядка сомножителей.
Множество S с определенной выше операцией умножения называют группой подстановок множества М.
Операция умножения на S обладает следующими свойствами. Во-первых, эта операция ассоциативна: для любых σi, σj, σk
(σi σj) σk = σi (σj σk).
Во-вторых, тождественная подстановка
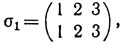
переводящая каждый элемент в себя, играет роль единицы в обычном умножении, а именно, для любой подстановки σi
σ1 σi = σi σ1 = σi.
Наконец, вместе с каждой подстановкой σi множество S содержит обратную ей подстановку σj, которая переводит число а в число b тогда и только тогда, когда σi переводит число b в число а. При этом, понятно, каждое из произведений σiσj и σjσi будет тождественной подстановкой:
σiσj = σjσi = σi.
Эти три свойства сохранятся, если распространить определение умножения подстановок множества {1, 2, 3} на случай подстановок любого конечного множества.
Более того, выяснилось, что имеются самые разнообразные системы объектов с операцией, обладающей указанными свойствами.
Это привело к следующему (общему) определению группы *).
*) (В виде, близком к современному, определение группы было впервые сформулировано английским математиком А. Кэли в 1854 году.)
Множество G, на котором определено умножение элементов, называется группой, если выполняются три аксиомы:
1. Умножение ассоциативно: для любых элементов а, b, с из G
a(bc) = (ab)c.
2. В множестве G существует такой единичный элемент е, что
еа = ае = а.
3. Для каждого элемента а множества G существует в G такой обратный элемент а-1, что
аа-1 = а-1а = е.
Обращаем внимание читателя на то, что в приведенном определении говорится об умножении элементов и используется связанная с обычным умножением терминология и символика. Этой "мультипликативной" терминологии мы и будем в дальнейшем придерживаться. Однако термин "умножение" нельзя понимать буквально; речь идет о любой операции, удовлетворяющей данным аксиомам. В частности, в ряде случаев естественнее называть операцию сложением и соответственно переформулировать аксиомы группы, пользуясь терминологией, связанной со сложением ("аддитивной" терминологией):
1. Сложение ассоциативно: для любых элементов а, b, с из G
(a + b) + c = a + (b + c).
2. Существует такой нулевой элемент 0, что для любого элемента а из G
а + 0 = 0 + а = а.
3. Для каждого элемента а существует такой противоположный элемент (-а), что
а + (-а) = (-a) + a = 0.
Группа подстановок, определенная выше, является, как мы видим, одним из примеров группы. Вообще взаимно однозначные преобразования любого множества образуют группу относительно операции умножения преобразований (эти группы сыграли основную роль в формировании общего понятия группы).
Читатель обнаружит далее, что многие примеры групп ему уже известны. Перечислим некоторые из них:
1. Множество всех ненулевых действительных чисел относительно операции умножения - "мультипликативная группа действительных чисел" R*.
2. Множество всех целых чисел относительно операции сложения - "аддитивная группа целых чисел" Z.
3. Множество всех векторов в пространстве относительно операции сложения векторов.
4. Множество всех многочленов с действительными коэффициентами относительно операции сложения многочленов.
Группы в примерах 1-4 имеют бесконечно много элементов, а группа S - конечная (6 элементов). Число элементов конечной группы называется ее порядком.
Из аксиом группы можно вывести, что в группе существует только один единичный элемент. Можно доказать также и единственность обратного элемента для всякого элемента группы.
Пример группы подстановок показывает, что умножение в группе может быть некоммутативным. Те группы, для которых операция коммутативна, так и называются коммутативными (примеры 1-4).
Если некоторое подмножество Н группы G само образует группу относительно операции, определенной в G, то подмножество Н называют подгруппой группы G.
Например, подмножества H1 = {σ1, σ2} и H2 = {σ1, σ4, σ5} группы S являются подгруппами этой группы. Подмножество четных целых чисел есть подгруппа аддитивной группы Z всех целых чисел, а подмножество нечетных чисел не будет подгруппой этой группы (сложение на Z не задает операцию на этом подмножестве, так как сумма двух нечетных чисел есть число четное).
Имеет место следующая теорема.
Для того чтобы подмножество Н являлось подгруппой группы G, необходимо и достаточно, чтобы выполнялись два условия:
1) произведение любых элементов h1, h2 из подмножества Н также является элементом из Н (h1h2 ∈ H);
2) если h ∈ H, то и обратный к нему элемент принадлежит H(h-1 ∈ H).
Наиболее просты так называемые циклические подгруппы, которыми обладает любая группа G. Со всяким элементом g ∈ G можно связать "порожденную" им циклическую подгруппу, которая, по существу, представляет собой наименьшую из подгрупп, содержащую данный элемент. Чтобы определить ее, введем понятие степени элемента g, полагая g0 = e и для любого натурального k
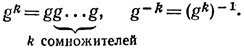
При таком определении степени выполняются хорошо знакомые нам правила действий со степенями: для любых целых чисел m и n
gmgn = gm+n, (gm)n = gmn.
Ясно, что всякая подгруппа, содержащая элемент g, должна содержать любые его степени. С другой стороны, уже само множество степеней образует, как нетрудно убедиться, группу.
Указанную группу называют циклической подгруппой, порожденной элементом g; ее обозначают символом (g), а сам элемент g называется образующим элементом этой группы.
Может случиться, что для некоторого элемента g циклическая подгруппа (g) совпадает со всей группой G, и тогда группа G также называется циклической. Например, аддитивная группа целых чисел есть циклическая группа с образующим элементом 1 (или -1), а ее подгруппа четных чисел - циклическая с образующим элементом 2. Являясь наиболее простыми, циклические группы служат важным инструментом для изучения групп, имеющих более сложное строение.
Между группой и любой ее подгруппой существует определенная связь, которую можно охарактеризовать с помощью понятия смежного класса по подгруппе.
Пусть H - подгруппа группы G и g ∈ G - произвольный элемент группы G (мы не требуем, чтобы он обязательно принадлежал подгруппе). Множество всевозможных произведений gh, где h - любой элемент подгруппы Н, называется смежным классом (точнее, левым смежным классом) по подгруппе H, а элемент g - его представителем, Обозначая левый смежный класс через gH, имеем, следовательно,
gH = {gh | h ∈ H}.
Аналогично определяются правые смежные классы Hg. Если группа G - коммутативная, то Hg = gH.
Для смежных классов, безразлично, левых или правых, справедливы два основных факта.
1. В случае конечной подгруппы H число элементов в любом смежном классе одно и то же и совпадает с порядком подгруппы.
2. Любые два смежных класса g1H и g2H либо совпадают, либо вовсе не имеют общих элементов.
Для иллюстрации понятия смежного класса рассмотрим следующий пример. Пусть Z - аддитивная группа целых чисел, а H - ее подгруппа, состоящая из чисел, кратных пяти. Тогда можно "выписать" следующие смежные классы:
H + 0 = {..., -10, -5, 0, 5, 10, ...},
H + 1 = {..., -9, -4, 1, 6, 11, ...},
H + 2 = {..., -8, -3, 2, 7, 12, ...},
H + 3 = {..., -7, -2, 3, 8, 13, ...},
H + 4 = {..., -6, -1, 4, 9, 14, ...}.
Читатель сразу же заметит, что это классы вычетов 0‾, 1‾, 2‾, 3‾, 4‾ по модулю 5. Легко видеть, что всякий смежный класс Н + n совпадает с одним из этих пяти, и что классы эти не пересекаются, Непосредственно видно также, что
Z = (H + 0) ∪ (H + 1) ∪ (H + 2) ∪ (H + 3) ∪ (H + 4).
Оказывается, то же самое верно для любой группы: если Hg1, Hg2, ..., Hgr - все различные (правые) смежные классы группы G по подгруппе H, то
G = Hg1 ∪ Hg2 ∪ ... ∪ Hgr.
В случае, когда G и H - конечные группы порядков m и n, из последнего равенства вытекает, что m = n · r. Мы пришли к следующей теореме Лагранжа *):
Порядок любой подгруппы конечной группы является делителем порядка группы.
*) (Лагранж (1736-1813) - великий французский математик; его труды по математическому анализу, механике и теории чисел имеют важнейшее значение для развития этих дисциплин. Лагранж - один из создателей дифференциального исчисления, классической теории дифференциальных уравнений и вариационного исчисления.)
Мы привели здесь простейшие определения и факты теории групп. За дальнейшими сведениями читатель может обратиться, например, к книгам [8], [9].
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'