Задачи и дополнения

1. Построить таблицу синдромов и соответствующих лидеров для (7,3)-кода с порождающей матрицей

2. Доказать, что алгоритм синдромного декодирования позволяет исправить любое количество ошибок, не превосходящее

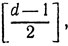
где d - кодовое расстояние.

Указание. Достаточно проверить, что все векторы веса

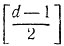
и меньше попадают в различные смежные классы и, следовательно, являются лидерами в своих смежных классах.

3. Код с проверочной матрицей

используется для исправления всех одиночных ошибок. Определить, какие еще ошибки могут быть в данном случае исправлены или обнаружены при декодировании по синдрому.

4. Проверить, что для обычного (нерасширенного) кода Хемминга лидеры ненулевых смежных классов исчерпываются всеми векторами веса 1. Верно ли это для расширенного кода Хемминга?