Игры на необычных досках

Шахматная игра создавалась на протяжении многих веков, и ее правила неоднократно менялись. С точки зрения математики различия в правилах игры, ходах фигур и форме доски не имеют принципиального значения.

Известно немало одних только национальных разновидностей шахмат. Самой древней шахматной игрой считается чатуранга, пришедшая из Индии и затем превратившаяся в шатрандж у арабов и шатранг у персов. До сих пор играют в японские шахматы (шоги), китайские (цюнь ки), корейские (тьян-кеун), армянские (гама), монгольские (шатар) и т. д. Эти игры (список их можно продолжить) больше относятся к истории шахмат, чем к математике, и не приводятся в книге.

Ниже мы рассмотрим ряд необычных шахматных игр, которые содержат те или иные математические элементы или носят занимательный характер. Прежде всего отметим, что игры могут отличаться от настоящих шахмат, во-первых, своей необычной доской, во-вторых, необычными фигурами и, в-третьих, необычными правилами игры. Разумееется, возможно присутствие двух "необычностей" или даже всех трех одновременно.

В этом разделе речь идет в основном об играх, которые получаются при изменении формы доски. Другие разновидности необычных шахматных игр рассматриваются в следующем разделе. Наконец, в третьем разделе рассказывается об играх, в которых преобладают математические элементы.

В нашей книге мы предпочитаем рассказывать о популярных играх, а не заниматься их классификацией с точки зрения математической теории игр. Но все-таки некоторыми научными терминами, пожалуй, стоит воспользоваться.

Шахматы, шашки и большинство их разновидностей относятся к разряду стратегических конечных игр с полной информацией. В этом смысле они ничем не отличаются от простейшей игры в крестики-нолики на доске 3*3. Структура таких игр теоретически абсолютно ясна. В каждом положении (позиции) у обеих сторон имеется конечное число ходов. Вся совокупность последовательностей ходов образует так называемое дерево игры. В любой позиции существует лучший ход, быть может не единственный. Последовательность лучших ходов за обе стороны (некоторая ветка на дереве) приводит воображаемую партию к однозначному результату, и поэтому исход игры в любом положении, в том числе в начале игры, является предопределенным. Но если в простейших крестиках-ноликах партия при наилучших ходах обеих сторон заканчивается вничью, то в других играх, прежде всего в обычных шахматах, вопрос о том, в чью пользу начальная позиция, по-видимому, навсегда останется открытым.

Процедура, которая дает оптимальную траекторию на дереве игры, называется минимаксной. Она лежит в основе многих переборных задач, возникающих не только при исследовании игр, но и при решении важных практических проблем, связанных с большим перебором вариантов. Сами эти проблемы изучаются в кибернетике, например в ее разделе "искусственный интеллект". Популярные игры, главным образом классические шахматы, служат удобной моделью для научных исследований, и поэтому их часто можно встретить в литературе по кибернетике.

Успешное решение переборных задач возможно только с помощью мощных компьютеров и современных методов программирования. Не случайно описание игр и их математический анализ можно найти и в книгах по программированию. Особой популярностью пользуются шахматы.

Минишахматы и максишахматы.Самый простой способ получить новую шахматную игру - изменить размеры доски, уменьшить или увеличить их. Игру в минишахматы М. Гарднер предлагает тем, кто желает сыграть в шахматы во время небольшого перерыва на работе. Доска 5*5 является минимальной, на которой умещаются все шахматные фигуры. Начальная расстановка такая: белые -Kpa1, Фb1, Ле1, Cc1, Kdl, пп а2, b2, с2, d2, e2; черные - Кра5, Фb5, Ле5, Сс5, Kd5, пп а4, b4, с4, d4, e4. Ходы обычные, лишь пешкам запрещено переступать сразу на два поля вперед. Любопытно, что даже при таких размерах доски весьма сложно определить, ничейна начальная позиция или одна из сторон должна победить.

При увеличении размеров доски никаких ограничений, разумеется, не существует. Можно рассматривать различные математические и шахматные игры и задачи на прямоугольных досках m*n, квадратных n*n и даже на бесконечных досках. Желающих сыграть на таких досках немного, эти игры используются, как правило, для придумывания интересных математических задач о маршрутах фигур, об их расстановках и перестановках на доске.

Если говорить о реальных шахматных играх, то среди прямоугольных досок рекорд принадлежит доске 16*12. Именно такие максишахматы предложил в свое время чемпион мира Хосе-Рауль Капабланка с целью преодолеть казавшуюся ему неотвратимой "ничейную смерть" шахмат. Игра на этой максидоске ведется удвоенным комплектом фигур, причем начальный ход пешки возможен сразу на четыре поля (со второй горизонтали на шестую для белых или с одиннадцатой на седьмую для черных). Для победы достаточно заматовать любого из королей противника.

Матч Капабланки с венгерским гроссмейстером Мароци в максишахматы, состоявшийся в 1929 году, закончился победой автора игры со счетом 3:1. Партии продолжались более ста ходов и тянулись часов по десять. Как показала жизнь, опасности "ничейной смерти" не существует, и изобретение Капабланки распространения не получило.

Среди досок большого размера можно упомянуть доску 12*12 для игры в так называемые великие шахматы, колыбелью которых была Индия. Каждый игрок имел по 12 фигур и 12 пешек, причем фигуры носили экзотические названия - крокодилы, жирафы, львы, единороги.

Известный завоеватель Тамерлан, страстный любитель шахматной игры, считал недостаточными обыкновенные размеры доски. Для шахмат его личной системы, которые именовались образцовыми, была изготовлена специальная доска 11*10; одиннадцать видов фигур (генерал, верблюд, рыцарь и др.) располагались на ней в три ряда.

Шахматы на параллельных досках. Идея "параллельных миров", часто используемая писателями-фантастами, не ускользнула и от внимания шахматных композиторов-фантастов. Игра ведется одновременно на двух досках, расположенных одна над другой. На каждой плоскости ходы обычные, но фигуры могут перемещаться и в пространстве с одной доски на другую. На рис. 15 показано, как король, ладья, слон, конь и пешка переходят с нижней плоскости (1) на верхнюю (2). Ферзь в пространстве ходит как король, пешке разрешается менять плоскость только при взятии. Желающие сыграть партию могут ограничиться одной доской, а фигуры, отправляющиеся на вторую плоскость, ставить на прозрачные стаканы или подставки, лежащие на исходной доске. Надеемся, впрочем, что геометрическое воображение позволит вам разобраться в рассматриваемых задачах без использования специальных приспособлений.

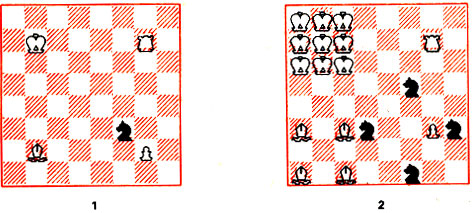
Рис. 15

В задаче на рис. 16 белые начинают и дают мат в 2 хода. 1. Лh7(1) - h8 (1). Единственный способ выждать события. Король черных неподвижен, и они могут ходить только конем или пешкой. Если отступает конь (на любую плоскость), то снимается удар с поля h5 и решает 2. Лh8(1) - h5(1)*! - ладью поддерживает белый конь. На 1... h4 (2) - h3 (2) следует 2. h2 (1) - h4 (1)*!, что было безопасно сразу ввиду взятия на проходе.

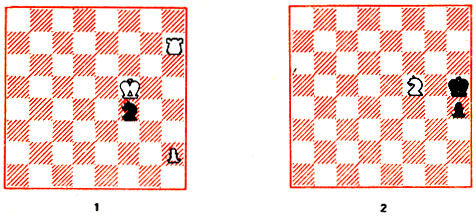
Рис. 16

Для решения задачи на рис. 17 - белые начинают и дают мат в 4 хода - надо внимательно осмотреть пространство. Приведем основной вариант. 1. Ке5 (2) - с5 (1) ! с угрозой 2. Кс5 (1) - b3 (1)*. Если 1...b6 (1):с5 (1),то 2. Kpcl (2) - с2 (1) Ла7 (1) - а7 (2). Ладья выходит из засады, но тут же на другую плоскость перебегает белая ладья. 3. Лb2 (2) - b2 (1) Ла7 (2) - а2 (2) 4. Лb2 (1) - b1 (1)*, или 3... Кра1(1) - а2(2) 4. Лb2 (1) - а2 (1)*. Проанализируем для примера заключительное положение во втором варианте. Черного короля на а2 (2) с нижней плоскости матует ладья а2 (1). Действительно, сама ладья находится под присмотром коня с2 (2), а поля b1, b2, b3 (обеих плоскостей) под контролем белого короля.

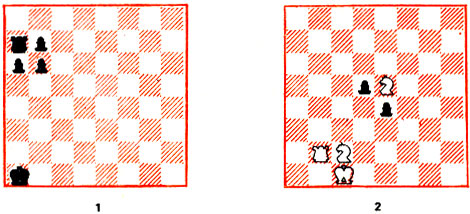
Рис. 17

Цилиндрические и тороидальные шахматы. Большинство рассматриваемых нами досок являются плоскими. Целый класс необычных досок получается, когда в "игру" вступает математика. При помощи различных геометрических или топологических преобразований стандартной доски нетрудно соорудить доски самой фантастической формы. Можно играть на цилиндрической и сферической доске, тороидальной, конусоидальной и даже на листе Мебиуса (обычная доска перекручивается на полоборота и склеиваются ее края). Шарообразная шахматная доска однажды как экспозиция участвовала на выставке авангардистов-художников.

Конечно, найдется немного желающих сыграть на перечисленных досках, однако некоторые их них весьма популярны среди шахматных композиторов-фантастов. При составлении и решении задач на таких досках не обязательно вооружаться ножницами и клеем, необходимые геометрические преобразования можно проводить мысленно.

Особой популярностью пользуются цилиндрические шахматы. Из обычной доски сооружаются две цилиндрические - вертикальная и горизонтальная. Первая получается приклеиванием вертикальных краев обычной доски, вторая - горизонтальных (рис. 18а, б). На цилиндрических досках получается не все, что возможно на обычной. Например, король и ладья, как правило, не в состоянии заматовать одинокого короля противника. С другой стороны, здесь открываются совершенно необычные возможности.

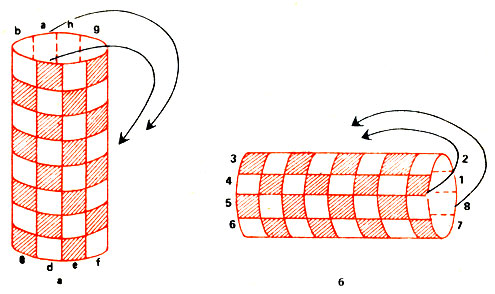
Рис. 18

В задаче на рис. 19 два задания. Белые ставят мат в два хода: а) на обычной доске; б) на вертикальной цилиндрической. В первом случае все просто - 1.Л: а6 Kpc1 2 Ла1*. Но на цилиндре после 1. Ла5:а6 теряется ладья - 1...h7:a6! (вертикали "а" и "h" приклеены!). Если же ладья уйдет с а5, то черные продвинут пешку, и мата нет. Решает 1. Ла5 - а5! - ладья совершает "круг почета" и возвращается на исходное место! На вынужденное 1... Kpb1 - c1 следует 2. Ла5 - a1*.

Рис. 19

В задаче на рис. 20 уже три задания. Белые ставят мат в один ход на трех досках: а) обычной; б) вертикальной цилиндрической; в) горизонтальной цилиндрической.

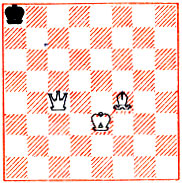
Рис. 20

Все три решения различны: а) на обычной доске решает 1. Фа6*, но не 1. Фа1 (h1) + Kpb7 (a7) 1; б) на вертикальном цилиндре линии "а" и "h" приклеены и 1. Фа6+ опровергается при помощи 1... Кра8 - h8! Матует здесь 1. Фс4 - а2 - h1*! Ферзь взял под контроль сразу четыре поля в районе черного короля (включая угловое) - а8, h7 по диагонали h1 - а8 и h7 по вертикали "h". Любопытно, что с более близкого расстояния отнять столько полей у короля, не становясь ферзем под бой, невозможно - ни на цилиндрической доске, ни тем более на обычной. Еще два поля для отступления черного короля - а7, b8 держит слон по диагонали c1 - h6 - а7 - b8. Итак, мы убедились, что на доске действительно матовая позиция. Легко проверить, что другие шахи ферзем не матуют: 1. Фе4 (с8, h7, g8) + Kph8 (h7, h7, b7)!

Заметим, что на шахматном цилиндре все диагонали одинаковые, то есть содержат (как вертикали и горизонтали) по восемь полей, причем геометрически каждая диагональ сворачивается в виток спирали. Так, на вертикальной цилиндрической доске на концах одного из таких витков оказываются поля а8 и h1, на концах другого - b8 и a1, третьего - с8 и b1 и т. д.

в) На горизонтальном цилиндре приклеены первая и восьмая линии и на 1. Фа6 + у короля есть ответ 1... Кра8 - b1! К цели ведет только 1. Фс4 - f1 - g8 - h7*! Вновь ферзь отнял у короля четыре поля: а8, b1 по диагонали h7 - b1 - а8 и а7, b7 по седьмой горизонтали. Поля Ь8, al держит слон по диагонали h2 - b8 - a1. Другие шахи ферзем не матуют - король уходит на а7 или b7.

Итак, в задаче всего четыре фигуры, а сколько занятных геометрических мотивов! Кстати, если на поле Ь7 добавить черного коня, то на обычной доске решение такое же - 1. Фа6*, а на цилиндрических маты уже иные; на вертикальном цилиндре 1. Фg8*, а на горизонтальном 1. Фа2*, причем пикантность матов в том, что они двойные, и перекрытия 1.... Kd8 (h8) и 1... Ка5 (а1) не спасают.

Рис. 21

Любопытная задача с таким же материалом на рис. 21. Белые начинают и дают мат в... 0 ходов. Это задание наверняка удивит читателя, а между тем мат ставится, причем сразу двумя способами. Для того чтобы добиться столь необычной цели, белые, как и требуется, не дотрагиваются ни до одной из своих фигур, но зато... сворачивают доску в цилиндр.

На любой из досок - горизонтальной или вертикальной - черный король сразу оказывается заматованным. Пусть приклеены друг к другу первая и последняя горизонтали. Тогда поле a1 присоединяется слева к диагонали b8 - h2, и поля b8, с7 попадают под наблюдение слона. Кроме того, в одну сливаются диагонали а6 - с8 и d1 - h5 (а6 и h5 - края новой диагонали), и в результате ферзь нападает на черного короля, отнимая у него и поле b7. Ну а поля d7, d8 недоступны королю на любой доске. Мат!

На вертикальном цилиндре поле a1 вновь присоединяется к диагонали b8 - h2, но снизу, а диагонали d1 - h5 и а6 - с8 опять сливаются (теперь края новой диагонали - d1 и с8). И снова черный король попадает в матовую сеть.

Многим знакома "задача о 8 ферзях", которой занимался великий математик К. Гаусс: сколькими способами можно расставить на шахматной доске восемь ферзей так, чтобы они не угрожали друг другу?

Оказывается, что если на обычной доске имеются 92 искомые расстановки, то на цилиндре уже нет ни одной! Докажем это для вертикальной цилиндрической доски. Возьмем обычную доску, помня, что ее края приклеены. Это означает, в частности, что поля с d1 до а4 и с h5 до е8 образуют одну диагональ. Запишем на каждом поле доски три цифры, совпадающие соответственно с номером вертикали, горизонтали и диагонали (параллельной а8 - h1), проходящих через это поле (рис. 22).

Рис. 22

Если восемь ферзей не угрожают друг другу, то на восьми полях, занимаемых ими, все первые цифры различны и, значит, образуют полный набор чисел 1, 2,..., 8. То же утверждение справедливо для вторых и третьих цифр. Значит, сумма всех 24 цифр, стоящих на полях с ферзями, равна (1+...+ 8)*3 = 108. Так как сумма цифр каждого поля делится на 8, то и найденная сумма должна делиться на 8, однако 108 на 8 не делится - противоречие!

Тороидальная доска получается в результате двойного склеивания краев обычной доски (см. стрелки на рис. 18, а, б). На такой доске одинокого короля не могут заматовать даже ферзь с королем - здесь просто нет ни одной матовой позиции.

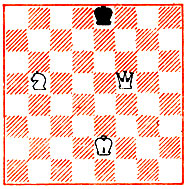
Рис. 23

На рис. 23 изображена одна из задач на тороидальной шахматной доске. Белые начинают и дают мат в 4 хода. После 1. Фf5 - h7! в распоряжении черных имеется два ответа: а) 1... Kpe8 - f8 (поля d1, e1 и f1 контролирует белый король с е2 - на торе действуют правила горизонтального цилиндра!) 2. Фh7 - g6 Kpf8 - e7 3. Kpe2 - e1 Kpe7 - d7 (поля d8 и f8 держит белый король с e1) 4. Фg6 - e8*!; b) 1... Kpe8 - d8 2. Фh7-c7 + Kpd8 - e8 3. Kb5 - h6! (конь идет по тору, как по вертикальному цилиндру!) 3... Kpe8 - f8 4. Фс7 - е1*! (поля f7 и g8 около черного короля держит белый конь, а остальные - ферзь).

Проективные шахматы. В проективные шахматы играют на проективной доске. Правила игры основаны на таких свойствах прямых линий, которые изучаются в проективной геометрии, где предполагается, что любое семейство параллельных прямых пересекается в так называемой бесконечно удаленной точке. В соответствии с этим доска для проективных шахмат получается из бесконечной доски (которая простирается по всей плоскости) добавлением четырех бесконечно удаленных полей: Р_Г - пересечение горизонталей, Р_В - пересечение вертикалей, P_Д1 - пересечение диагоналей, параллельных a1-h8, Р_Д2 - пересечение диагоналей, параллельных a8-h1.

На проективной доске сохраняются многие правила обычных шахмат, а основное изменение состоит в том, что дальнобойная фигура может переместиться на бесконечно удаленное поле (с учетом ее способа передвижения) и оттуда вернуться на конечное поле доски.

Рис. 24

Рассмотрим одну задачу на проективной шахматной доске (рис. 24). Белые начинают и дают мат в два хода. Первый ход решения 1. Kph2 -g 1! Теперь у черного короля несколько ответов. Если он идет на е4, то мат дает ферзь, удаляясь в бесконечность через а5: Фс5 - Р_Г*. Действительно, с поля Р_Г ферзь нападает на черного короля и держит все поля вокруг него: е3, f3 - через h3, d4, e4, f4 - через h4; d5, e5, f5 - через а5. Ход 2. Фс5 - Р_Г матует и при 1... Kpf4 - f3. Поля е4, f4, g4 в этом случае ферзь держит через b4; еЗ, f3, g3 - через h3, a e2, f2, g2 - через h2 (белый король предусмотрительно ушел с b2).

При отступлении черного короля на линию "g", а также при 1... d3-d2 матует 2. Фс5 - Р_Д1* (ферзь уходит в бесконечность по диагонали с5-а3). Например, после 1... Kpf4 - g5 2. Фс5 - Р_Д1* поля f4, g5, h6 ферзь держит через c1; поле f6 - через al; поле f5 - через h7; поля g4, h5 - через d1; и поле b4 - через e1.

Осталось рассмотреть ходы черных коней. На любой ход коня b6 следует 2. Фс5 - Р_Д2*, а на любой ход коня с7 - 2. Фс5 - Р_В* (в первом случае ферзь уходит в бесконечность через а7, во втором - через с8).

Для задачи-двухходовки важно не только наличие решения, но и его единственность. Нетрудно убедиться, что при других вступлениях белым уже не удастся поставить мат на втором ходу. Так, после 1. Фс5 - Р_Г+ черный король скрывается на g5, а после 1. Фс5 - Р_Д1 на е4, с поля Р_Д2 ферзь даже не дает шаха, а хода Фс5 - Р_В и вовсе нет (вертикаль "с" загорожена с обеих сторон). Любопытно, что в решении задачи использовались все четыре бесконечно удаленных поля проективной шахматной доски.

Объемные шахматы. Поля досок, которые мы рассматривали до сих пор, определялись двумя координатами, то есть использовалась обычная шахматная нотация (лишь в игре на параллельных досках обозначения были чуть сложнее). Иначе обстоит дело в объемных (пространственных) шахматах. В них играют на трехмерной доске, представляющей собой параллелепипед m*n*k (в частности, куб n*n*n), единичные кубики которого образуют "поля" доски. Эти поля записываются уже тремя координатами. Возьмем, например, объемную доску 4*4*4, содержащую, как и обычная, 64 поля, но только объемных (64 кубика). Если четыре горизонтальных слоя такой доски занумеровать числами 1, 2, 3, 4, то ее левый ближний столбец содержит поля a11, а12, а13, а14 и т. д. Перемещению вдоль слоя объемной доски соответствует ход на обычной доске, но фигуры могут перескакивать также из одного слоя в другой. Так, ферзь с поля a11 в состоянии двигаться не только обычными маршрутами до полей а41 и h11, но может попасть и на верх доски - на поле а14 или пройти по ее большой диагонали a11-h44. Конь на объемной доске тоже ходит буквой Г: на одно поле в одном слое и на два в перпендикулярном.

Мы уже говорили о задаче "о восьми ферзях", которой интересовался К. Гаусс. Еще одной математической задачей на шахматной доске - "о ходе коня" увлекался другой великий математик Л. Эйлер. Требуется обойти конем все поля обычной шахматной доски так, чтобы ни одно из них не посетить дважды. Известно много методов обхода доски указанным образом, в том числе предложенных Эйлером, однако общее число маршрутов до сих пор не установлено (доказано, что оно превышает 30 миллионов!).

Следующая задача обобщает классическую задачу о ходе коня. Обойти конем все поля объемной шахматной доски 4X4X4, посетив каждое из них по одному разу.

Рис. 25

Найти маршрут коня на объемной доске равносильно тому, чтобы последовательно занумеровать все ее поля-кубики числами от 1 до 64 так, чтобы каждые два поля с соседними номерами были связаны ходом коня. На рис. 25 представлены проекции четырех горизонтальных слоев объемной доски на плоскую доску 4*4 (слои имеют номера 1, 2, 3, 4). Нетрудно убедиться, что, отправляясь от поля b33 (с номером 1) и двигаясь конем в указанной последовательности, мы обойдем все поля доски 4*4*4.

Гексагональные шахматы. Нестандартные доски редко используются для серьезной игры, это, скорее, инструмент для композиторов-фантастов. Но есть и одно исключение - гексагональные, или иначе, шестигранные, шахматы. Доска, как и ее поля, имеют вид шестиугольника, и фигуры получают намного больше простора. Изобретены два варианта игры, один - советским геологом И. Шафраном, другой - польским инженером В. Глинским. Польские шахматы получили довольно широкое распространение в мире. Расскажем сначала о них.

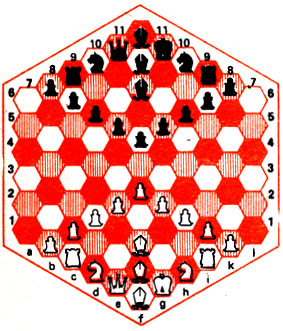
Рис. 26

Гексагональная доска состоит из 91 поля трех цветов - белого, черного и серого; на ней 11 вертикалей от "а" до "l" (кроме "j")> поля каждой нумеруются снизу вверх (рис. 26). На крайних вертикалях по 6 полей, на центральной - 11. Роль горизонталей выполняют диагонали, слева от линии "f" параллельные а1 - f1, а справа параллельные f1 - 11. В дополнение к обычному комплекту фигур каждая сторона получает по одному слону - серопольному и одной пешке. Начальное расположение показано на рис. 26, а ходы фигурна рис. 27. Король, как и полагается, ходит на все соседние поля - не только непосредственно примыкающие к данному, но и на ближайшие к нему того же цвета. Таким образом, с f3 он может пойти на одно из 12 полей, указанных стрелками. Столько же полей и в распоряжении коня, стоящего на f8. Ладья и слон перемещаются на любое число полей в одном из шести направлений (разных для этих фигур). Ферзь, объединяющий ходы ладьи и слона, движется в тех же 12 направлениях, что и король, но на произвольное число полей. Конечно, ближе к границе доски число ходов для всех фигур уменьшается. Пешки ходят на одно поле по вертикали (в начальном положении на два), бьют наискосок: с b5 на а5 и с6 (рис. 27). Сохраняется и взятие на проходе - в ответ на с2 - с4 черная пешка d3 может побить белую d3:c3. Достигая последнего поля вертикали, пешка превращается в любую фигуру. Рокировок нет, так как короли находятся в достаточной безопасности, а ладья за два хода подключается к атаке или защите. Все остальные правила, в том числе цель игры - поставить мат неприятельскому королю, не меняются.

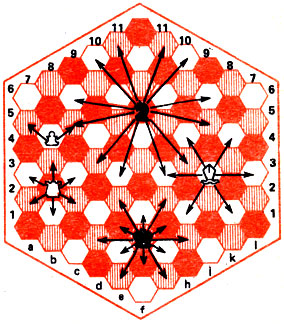
Рис. 27

Доска для шахмат Шафрана изображена на рис. 28, она получается из польского варианта отбрасыванием линий f1-11, f2-16 и двух правых вертикалей k1-k7 и 11-16; число полей сокращается до 70. Начальная расстановка (рис. 28) напоминает обычные шахматы, а фигуры ходят, как на рис. 27, лишь пешка бьет под углом 60º: с b5 на а6 и с7. Пешки трех центральных вертикалей могут сделать первый ход сразу на три поля вперед, остальные - только на два. В данной игре возможны рокировки - короткая, если ладья приближается к королю, и он переступает через нее, и длинная, если король подходит к ладье, и она перепрыгивает через него.

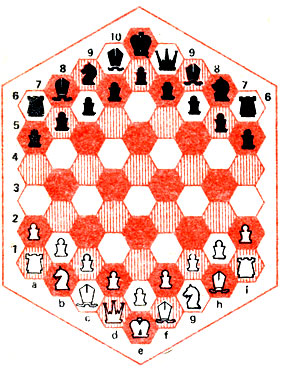
Рис. 28

В польских шахматах доска представляет собой правильный шестиугольник, и, возможно, такая геометрическая четкость помогла Глинскому "обыграть" Шафрана в популярности игры. В шахматах Шафрана партия может закончиться уже на третьем ходу: 1. Кb1 - с4 Kc8 - d6 2. Фd1 - е3 b6-b5 (черные хотят прогнать неприятельского коня, но их ждет горькое разочарование) 3. Kc4 - d7*! В шахматах Глинского возможен только "детский", 4-ходовый мат: 1. Фе1 - с3 Фе10 - с6 2. Kh1 - i3 Kh9 - i6 3. Ki3 - g6 е7-е6 4. Фс3: f9*, или 3... Ki6 - g5 4. е4-е5 Фс6:f3*. Забавно, что в этой игре шах дается уже на первом ходу: 1. Kpg1 - g2 Cf10 - d6+.

В классических шахматах дебюты исследованы глубоко, самостоятельное творчество нередко начинается только после 15-20 ходов. Теория шестигранных шахмат почти не разработана, к тому же разнообразие ходов и вариантов столь велико, что предугадать ответ противника труднее, чем в обычных шахматах. Увеличились размеры доски и как следствие подвижность фигур, у любителей тактики теперь больше возможностей для комбинаций.

Немного хроники. В 1953 году польские шахматы демонстрировались на Всемирной выставке в Париже. В 1980-м в Лондоне состоялся первый чемпионат Европы. Тогда же был организован и всесоюзный клуб "6 граней", который с 1982 года проводит соревнования. В 1984-м в Венгрии прошел второй чемпионат Европы, в котором участвовали 26 игроков из 7 стран. Победителям первого первенства поляку М. Мацковяку и второго - венгру Л. Рудольфу присвоено звание международного гроссмейстера по гексагональным шахматам.

Геометрия шестигранной доски весьма своеобразна. Так, вертикаль "f" является ее осью симметрии, а поле f6 - центральным полем (на стандартной доске центр состоит из четырех полей - d4, d5, e4, e5). Хотя доска больше, чем обычная, но путь коня между произвольными двумя полями занимает не более четырех ходов (на доске 8*8 конь с a1 до h8 добирается за 6 ходов). Любая фигура на гексагональной доске может сделать ход, сохраняя контроль над прежними полями. Особенно интересно проявляется это свойство у коня. Например, находясь на g9, он атакует поле е7, но, перескочив на d9 или h6, продолжает контролировать его. Получается, что конь в состоянии пройти по треугольнику, выигрывая темп у партнера. В обычных шахматах коня для такой цели использовать невозможно.

Вот еще некоторые отличия польских шахмат от традиционных. Один король на гексагональной доске в состоянии запатовать неприятельского короля, если тот находится в углу. Например, белый король f3 полностью сковывает действия черного короля П. Из этого следует, что король f1 и любая фигура могут дать мат одинокому неприятельскому королю. С другой стороны, загнать короля в угол нелегко даже двумя легкими фигурами, для победы необходима третья. Зато ферзь без всякой поддержки может поставить мат, скажем, с того же поля f3 королю f1.

Рассмотрим три задачи на польской гексагональной доске.

В задаче на рис. 29 белые начинают и дают мат в 4 хода.

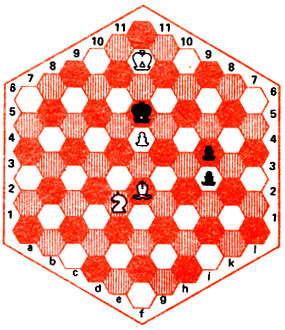
Рис. 29

В обычных шахматах конь, совершающий ход, теряет контроль над полями, которые только что были в его распоряжении. Иное дело в гексагональных...

В данной позиции черный король запатован: поля е6 и g6 держит белый слон, е7 и g7 - пешка, е8, е9, f7, g7, g8 - король, сама пешка f7 находится под защитой коня. Но ведь белым надо ходить...

1. Ке4 - с5! Конь сдвинулся с места, но не выпустил из-под контроля пешку f7,- хитрый прием, уже упомянутый 1 выше. 1... i4-i3 2. Kc5 - d8! Вновь пешка под защитой коня. 1 Не годится 2. Ке4? из-за 2... i4! и мата нет, но не 2... i2. 3. Kh4 и 4. Ki6*.

2... i3-i2 3. Kd8 - g9 i2 - i1Ф 4. Kg9 - i6*! Конь сделал 1 четыре подряд хода, но пешка все время находилась под его защитой!

В задаче на рис. 30 белые начинают и дают мат в 2 хода. На первый взгляд у черного короля достаточная свобода, и за два хода его не пленить...

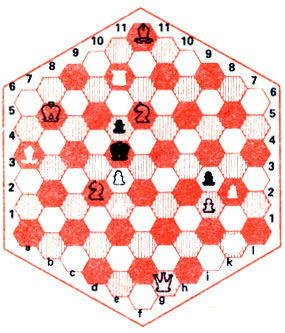
Рис. 30

1. Cf11-11! Неожиданное перемещение слона из угла в угол шестиугольной доски решает дело. Черные в цугцванге. Любой ход их короля ведет к красивому мату ферзем в центре доски. 1... Kpe6:d4 2. Фg1-c2*. Пригодился слон, который взял под прицел поле с2. 1... Kpe6:f8 2. Фg1-g9*. Поле g7 тоже контролируется слоном, притаившимся вдали от места основных событий. 1... Kpe6-f5 2. Фg1-g3*. И поле g3 в зоне действия слона. 1... Kpe6-d6 2. Фg1-с6*. В последнем варианте белого ферзя поддерживает король.

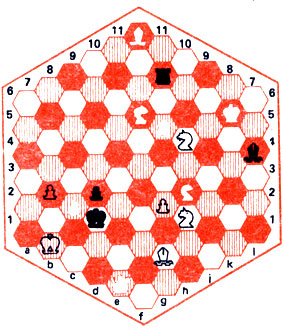
Рис. 31

И на рис. 31 белые начинают и дают мат в 2 хода. Эта задача иллюстрирует геометрическую тему Новотного (перекрытие), довольно распространенную в обычной шахматной композиции. Разница лишь в иных линиях действия фигур.

1. g4-g6! Пешка стартует сразу на два поля вперед. Попутно возникает еще один задачный элемент - освобождение поля для другой фигуры. Теперь пешка оказалась в точке пересечения линий g1-g10 и а4-14, находящихся соответственно в распоряжении ладьи и слона. 1... Ch4:g6. Траектория ладьи перекрыта и 2. Kh6-g4*. 1... Лg9:g6. Траектория слона перекрыта (линия а4-14 ле принадлежит компетенции ладьи) и 2. Kh6-e6*.

Шахматы для нескольких игроков. Почти все игры, рассматриваемые в книге, в том числе шахматы, по терминологии математической теории игр представляют собой игру двух лиц, то есть в них играют два человека. В упомянутых до сих пор разновидностях шахмат предполагалось наличие двух участников, однако известно немало шахматных игр, в которые могут одновременно играть три или четыре игрока. Так, в одном из вариантов шахмат "на троих" доска представляет собой шестиугольник с 96 полями, а фигуры трех, цветов - белые, черные и красные. Выигрывает тот, кто берет королей обоих соперников. Игра построена таким образом, что позволяет двоим партнерам объединяться против более сильного.

Интересно, что в своем первоначальном виде шахматы были предназначены для четырех игроков. Речь идет о старинной игре чатуранга, в которую играли двое на двое (желтые и красные боролись с черными и зелеными). Вряд ли стоит описывать правила чатуранги, поскольку в наше время эта игра имеет лишь исторический интерес.

Четверо шахматистов сражались когда-то и в "королевскую игру", доска для которой имела форму креста и состояла из системы линий, пересекающихся по, вертикалям, горизонталям и диагоналям. Сейчас королевская игра совсем забыта, а название сохранилось в виде синонима для обыкновенных шахмат.

Из игры с четырьмя участниками шахматы постепенно превратились в игру для двух человек. Хотя современные шахматы завоевали всеобщее признание, игра для четверых полностью не забыта. В так называемые четверные шахматы играют на 160-клеточной доске, которая получается из доски 8*8 добавлением к каждому краю трех горизонталей - на двух крайних из них расставляются фигуры стандартным образом, всего четыре обычных комплекта. Играют двое на двое, причем члены одной команды сидят напротив друг друга или рядом. Известны различные виды четверных шахмат, они отличаются не только расположением участников около доски, но и правилами игры, территорией, на которой разрешено действовать, цветом фигур. Любопытно, что в одном варианте игры заматованный король снимается с доски, в другом остается на ней и может быть разматован союзником. Четверные шахматы официально признаны в нашей стране, и по ним даже было проведено несколько чемпионатов столицы.

Если у вас собралась шахматная компания из четырех человек, все жаждут играть, а ничего, кроме одной, самой обыкновенной доски под рукой нет, не отчаивайтесь. Играйте двое на двое обычную партию, но ходы делайте по очереди, через одного. Это очень веселая игра, и не беда, если один из двух членов команды задумает интересную идею, а другой сразу же ее погубит.

Итак, для четырех игроков придумано много шахматных игр. Однако рекорд числа действующих лиц принадлежит "астрономическим шахматам", распространенным в глубокой древности. В них играли семь человек на круглой доске, а фигурами были планеты и звезды (Луна, Солнце, Венера, Марс и т. д.).