Быки и коровы

Эта логическая, комбинаторная игра, придуманная сравнительно недавно, в 70-е годы, завоевала огромную популярность во многих странах. Ее наиболее распространенный вариант выпускается в виде комплекта под названием "Mastermind" (мастермайнд, буквальный перевод - "выдающийся ум"). Но начнем наш рассказ с "быков и коров".

Играют двое. Каждый задумывает четырехзначное число с разными цифрами, которое должен отгадать партнер (на первом месте может стоять и 0). Ход заключается в том, что отгадывающий называет определенное число, также четырехзначное с разными цифрами. Если задуманное и названное числа имеют общие цифры, стоящие на одних и тех же местах, то такую ситуацию называют "быком" (далее обозначается "б"). Если общие цифры есть, но стоят они на разных местах, то это "корова" (обозначается "к").

В ответ на ход партнера загадчик сравнивает свое число с названным и сообщает общее число "быков" и "коров". Например, если задумано 5239, а названо 2735, то ответ будет "1 бык 2 коровы" (16 2к). Цифра 3 имеется в обоих числах и стоит на одинаковых местах (16), цифры 2 и 5 общие, но стоят на разных местах (2к), цифры 7 и 9 не являются общими.

Сделав ход и получив ответ, отгадчик извлекает некоторую информацию о задуманном числе и в конце концов определяет его. Игра заканчивается в тот момент, когда на очередной свой ход он получает ответ 46, то есть задуманное число найдено. Выигрывает тот, кто быстрее отгадает число противника.

Приведем один пример. Ходы и ответы на них будем записывать в табл. 1.

Таблица 1

Предположим, что партнер задумал число 3594, которое нам нужно отгадать. Наш первый ход 1568 дал ответ 16. Это означает, что в задуманном числе имеется всего одна цифра из названных, причем стоящая на своем месте. Постараемся отгадать ее, не привлекая пока - чтобы не запутаться - другие цифры. Сделаем второй ход 1586. Ответ 16 говорит о том, что на своем месте стоит цифра 1 или 5. Теперь следует третий ход 1658, и ответ 1к показывает, , что в задуманном числе на втором месте стоит 5, а цифр 1, 6, 8 в нем нет. Ходом 2570 постараемся выяснить наличие цифр 2, 7 и 0. Ответ 16 весьма удачен - этих цифр в искомом числе нет. Итак, ясно, что задуманное число состоит из цифр 3, 4, 5, 9, причем на втором месте - 5. Сделаем следующий ход 4539. Ответ 16 3к означает, что задумано одно из чисел - 3594 или 9543. Если первая цифра 3, то 9 может быть только третьей, а если первая 9, то 3 - только четвертой. Ход 3594 и ответ 46 привел нас к цели; ответ 16 3к означал бы, что задумано число 9543, в этом случае партия продлилась бы на ход дольше.

Чем отличаются "быки и коровы" от мастермайнда? В комплекте мастермайнда роль цифр выполняют колышки шести цветов (красные, желтые, синие, зеленые, белые, черные), они вставляются в отверстия доски, которая выглядит примерно так, как показано на рис. 1. Задуманный набор кодовых колышков - цифр (вверху доски) шифровальщик загораживает специальными воротами, и он не виден расшифровщику. Для каждого хода также предусмотрены четыре отверстия, а еще четыре отверстия, размером поменьше, расположены слева - для ответа на него. Ход состоит в том, что отгадчик вставляет в отверстия четыре цветных колышка, а загадчик в ответ выставляет маленькие ключевые колышки двух цветов (черные и белые) в отверстие слева от хода (в любом порядке). Черные колышки выполняют роль "быков", а белые "коров". Если угаданы не все цвета, то некоторые отверстия остаются пустыми.

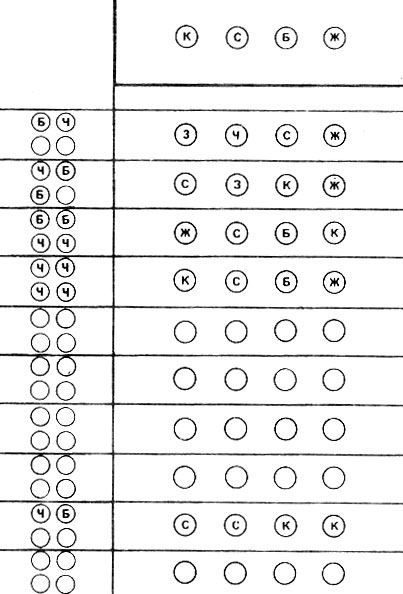
Рис. 1

В примере на рис. 1 избран шифр ксбж. При первом ходе зчсж произошло одно полное совпадение (ж) и один цвет (с) оказался не на своем месте. Таким образом, ответ бч (по-старому 16 1к). На втором ходу ответ чбб, на третьем - ббчч (определены все четыре цвета), на четвертом - чччч. Игра закончена. Партия длилась четыре хода. Вообще, как мы видим, доска рассчитана на десять ходов - (только совсем неопытные игроки не укладываются в эти рамки).

В переводе мастермайнда на язык "быков и коров" мы получаем, что задуманное число и числа-ходы разрешается образовывать только из шести цифр (шесть цветов колышков). Правда, цвета колышков в шифре и ходах могут повторяться (в отличие от "быков и коров", где все цифры разные). Так, на рис. 1 в девятой строке сделан ход сскк. Ответ на него чб (синий цвет на своем месте, красный не на своем). Оба цвета считаются только один раз. При шифре ккбж и том же ходе сскк красный цвет считался бы уже дважды, и ответ бб.

Сформулируем более точно, как дается ответ на каждый ход в мастермайнде. Сначала сравниваются цвета первых колышков шифра и хода. Если они совпадают, ставится черный кодовый колышек ("бык"), а первые колышки шифра и хода исключаются из рассмотрения. Если они разные, сравниваются цвета первого колышка шифра и второго колышка хода. При совпадении ставится белый кодовый колышек ("корова"), а первый колышек шифра и второй хода исключаются из рассмотрения. Если цвета разные, сравниваются цвета первого колышка шифра и третьего колышка хода и т. д. Когда первый колышек шифра будет исключен из рассмотрения (либо сам по себе, либо при одном из совпадений цветов - вместе с соответствующим колышком хода), точно так же последовательно сравнивается цвет второго колышка шифра с цветами колышков хода, а затем аналогично третий и четвертый колышки шифра. Очевидно, для шифра и ходов на рис. 1 наша процедура даст те же ответы.

Хотя описание занимает много места, на самом деле ответ формулируется за несколько секунд.

Мастермайнд отличается внешней привлекательностью - красивая доска, разноцветные колышки, ворота и т. д. Однако у "быков и коров" другое преимущество - для игры не нужно ничего, кроме бумаги и карандаша. Впрочем, и в наших магазинах появился в продаже комплект мастермайнда под названием "Мыслитель", так что теперь есть выбор...

Ниже мы упомянем о некоторых компьютерных достижениях в рассматриваемых играх. При составлении машинной программы для мастермайнда различные цвета колышков нужно прежде всего закодировать числами, то есть так или иначе мы вынуждены прибегнуть к цифровому языку "быков и коров".

Для отгадывания числа в "быках и коровах" или шифра в мастермайнде партнер должен как бы придумать тест для разгадывания числа или шифра. Таким образом, обе наши игры относятся к разряду тестовых.

Загадывая число в "быках и коровах", его первую цифру можно выбрать десятью способами, вторую - девятью (одна цифра занята), третью - восемью, наконец, четвертую - семью, всего имеем 10*9*8*7 = 5040 различных чисел. В мастермайнде на любом месте может стоять колышек любого цвета (из шести возможных), то есть всего 6⁴ = 1296 вариантов.

Итак, в "быках и коровах" имеется 5040 различных чисел, которые можно загадывать и которыми можно ходить. А сколько существует различных ответов? Все они указаны во втором столбце табл. 2, их 14 (очевидно, ответ 36 1к невозможен). Горизонтальной чертой в таблице разделены случаи, в которых обнаружены все четыре цифры, три цифры, две, одна и ни одной. В третьем столбце указано количество чисел, которые могут дать соответствующий ответ на первом ходу. Самый приятный ответ, конечно, 46, сразу заканчивающий игру. Как мы видим, наибольшее разнообразие возможных чисел остается при ответе 1к - 1440.

Разумеется, результат игры, то есть количество ходов, за которое отгадывается задуманное число, в какой-то степени зависит от случая. Но многое определяется и искусством играющих. Здесь возникает вопрос: что понимать под мастерством игры в "быки и коровы"? Ведь даже начинающий игрок уже первым ходом может случайно отгадать задуманное число, но это еще не говорит о его умении.

Предположим, игроки А и Б сыграли матч из трех партий. Игрок А во всех трех партиях отгадал число партнера за 5 ходов. Игрок Б в двух партиях отгадал число за 4 хода, а в одной за 9. Кто играет лучше? Игрок Б выиграл матч со счетом 2:1, но ведь общее число ходов у него больше. Если, скажем, в шахматах важна сама победа независимо от продолжительности партии, то в "быках и коровах" именно скорость отгадывания, количество затраченных ходов собственно и составляют результат игры.

Рассмотрим два наиболее интересных подхода к оценке силы игры в "быки и коровы". Обозначим через l_i, число ходов, за которое данный игрок отгадывает число с номером i (i пробегает значения от 1 до 5040). Введем две характеристики его силы игры в "быки и коровы":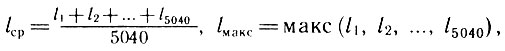

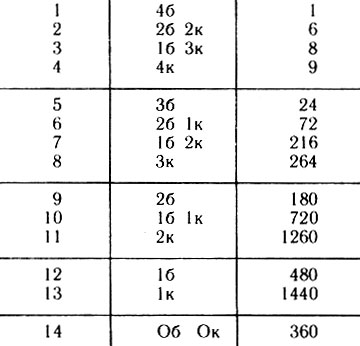
Таблица 2

где l_ср - среднее число ходов, за которое игрок отгадывает число, а l_макс - число ходов, гарантирующее ему раскрытие шифра. Любое число отгадывается им самое большее за l_макс ходов. Каждая из этих двух характеристик, по желанию, может служить для оценки силы. Очевидно, величины l_ср и l_макс точно так же определяются и для мастермайнда, только в формулах будет фигурировать другое число - 1296.

В игре людей всегда легко разобраться, кто сильнее. Другое дело, когда речь идет об ЭВМ. Для произвольной стратегии игры, сформулированной в виде некоторого алгоритма, можно вычислить числа l_ср и l_макс и, значит, в зависимости от критерия определить, какая программа для ЭВМ сильнее.

Стоит заметить, что игры, о которых идет речь, представляют собой весьма интересный объект для исследования на компьютере. Достаточно сказать, что в написании программы для "быков и коров" участвовал один из крупнейших в мире специалистов в области программирования американец Д. Кнут. В нашей стране ряд результатов в этой области был получен группой студентов кафедры кибернетики МИСиС под руководством доцента М. Гендлера.

Основная задача, привлекающая математиков и программистов, состоит в нахождении оптимального алгоритма, то есть такой стратегии игры, при которой число l_ср или соответственно l_макс принимает наименьшее значение. Если говорить об l_ср, то здесь полной ясности цока нет. Найдены стратегии, которые для мастермайнда дают значение l_ср чуть меньше 4, а для "быков и коров" - чуть больше 5, но вопрос об оптимальных алгоритмах остается открытым.

Что же касается числа l_макс, представляющего больший интерес, то проблема полностью решена. Для мастермайнда построен наилучший алгоритм игры, при котором любое число шифровальщика разгадывается на позднее пятого хода, и доказано, что для любого другого алгоритма (стратегии) найдется хотя бы одно число, на разгадку которого уйдет не меньше пяти ходов. Таким образом, l_макс = 5.

Для "быков и коров" несколько лет назад студентами МИСиС была разработана стратегия, гарантирующая отгадывание любого числа за семь ходов, и было установлено, что l_макс≥6. Но сомкнуть эти границы никак не удавалось. И вот совсем недавно при помощи весьма хитроумных комбинаторных рассуждений и тонкого использования машинных возможностей они определили, что l_макс = 7. Иначе говоря, построен алгоритм игры в "быки и коровы", позволяющий найти любое загаданное число за семь ходов, и доказано, что шестиходовой стратегии не существует.

Кстати, в приведенном в самом начале примере задуманное число было отгадано именно за семь ходов (хотя пример носил учебный характер и не ставилась цель играть оптимально).

Конечно, нас не должен удивлять тот факт, что для "быков и коров" числа l_ср и l_макс больше, чем для мастермайнда,- ведь в первом случае возможных вариантов шифра почти в 4 раза больше. Впрочем, известен усложненный вариант игры - супермастермайнд, в котором вместо четырех отверстий используются пять и вместо шести цветов кодовых колышков - восемь.

Рассмотрим теперь несколько партий (точнее было бы сказать, пользуясь шахматной терминологией,- окончаний или этюдов), представленных в виде задач. Разобрав их, вы получите неплохую иллюстрацию тонкостей игры в "быки и коровы". Будут изучены все ситуации, когда ответ противника на наш первый ход - для определенности число 1234 - совпадет с одним из первых пяти в табл. 2. При ответе 46 партия продолжается всего один ход, а для каждого из четырех других случаев мы укажем способ игры, гарантирующий отгадывание задуманного числа за наименьшее количество ходов. Другими словами, за столько ходов мы точно отгадаем число противника, каким бы оно ни было, а при меньшем количестве нам всегда может не повезти - шифр не будет раскрыт.

Таблица 3

Партия 1. На первый ход 1234 противник ответил 2б 2к. Какое наименьшее количество ходов гарантирует отгадывание задуманного числа?

Легко проверить, что только шесть задуманных чисел в ответ на первый ход 1234 могут дать ответ 2б 2к (табл. 3, первый столбец), и при любом втором ходе по крайней мере три из них дадут одинаковый ответ.

Вторым ходом сыграем 1356 (вместо цифр 5 и 6 можно было бы взять и другие, отличные от 1, 2, 3, 4). Все возможные ответы находятся во втором столбце таблицы. Ответ 2б сразу определяет задуманное число - 1324 (у других чисел иной ответ), ответ 1б 1к оставляет два варианта, а ответ 2к - три. Третий ход 3256 (с учетом второго) вносит полную ясность - все пять чисел-кандидатов дают разную пару ответов. Прочерк в табл. 3 (и всех последующих таблицах) означает, что при соответствующем ходе "реакция" на него данного числа нас уже не интересует. Таким образом, на четвертом ходу гарантирован ответ 4б и партия длится не более четырех ходов.

Типичная и совершенно не очевидная ошибка, которую допускают многие, кто решает эту задачу, состоит в использовании для игры чисел, содержащих только цифры 1, 2, 3, 4. Логика здесь простая - раз все цифры известны, то зачем подключать новые? Однако при таком подходе задуманное число с гарантией определяется на пятом ходу (ответ 4б).

Партия 2. Тот же вопрос, что и в первой партии, но ответ на первый ход 1б 3к.

На первый ход 1234 восемь чисел могут дать ответ 1б 3к (табл. 4). При любом втором ходе хотя бы одна четверка

чисел дает один и тот же ответ, и для выяснения ситуации понадобятся еще два хода. При втором ходе 1256 числа разделяются на две группы; для чисел первой группы (ответ 1б 1к) сделаем третий ход 1563, а для чисел второй группы (ответ 2к) - ход 2564. После этого остаются две пары чисел в каждой группе, требующие еще одного хода, и четвертый ход 1564 полностью проясняет картину. Таким образом, вторая партия длится не более пяти ходов.

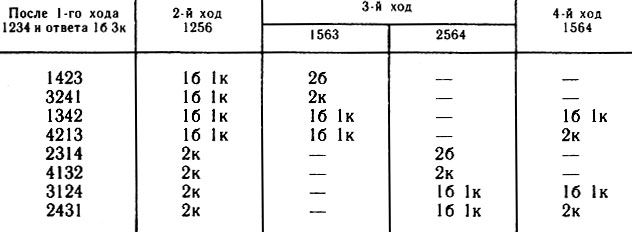
Таблица 4

Партия 3. Тот же вопрос, что и в предыдущих двух партиях, но при ответе на первый ход 4к.

В ответ на первый ход 1234 девять чисел могут дать ответ 4к (табл. 5). Второй ход 3102 расшифровывает два числа, а остальные семь делит на две группы, в одной из которых решает ход 4153, а в другой - 2456. Четвертый ход завершит партию (будет получен ответ 4б).

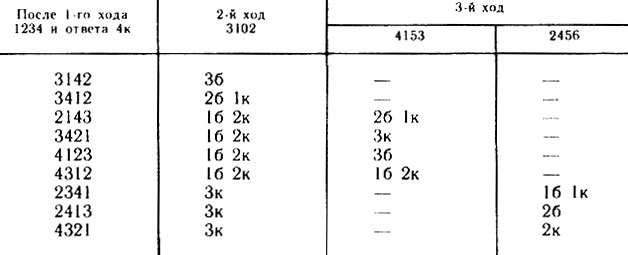
Таблица 5

Партия 4. Тот же вопрос, что и в предыдущих трех партиях, но при ответе на первый ход 3б.

Ответ 3б на первый ход 1234 дают 24 числа. Действительно, три цифры можно зафиксировать на своих местах четырьмя способами, а для четвертой имеется шесть возможностей: О, 5, 6, 7, 8, 9, то есть всего 4*6 = 24 варианта. Любопытно, что найти задуманное число среди 24 чисел в данной партии удается за столько же ходов, за сколько восемь чисел во второй партии.

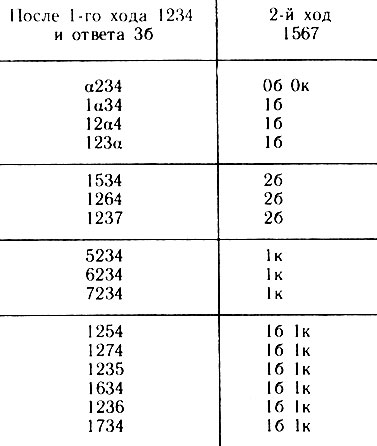
Таблица 6, а

Таблица 6, б

Рассмотрим табл. 6 а. В ее первых четырех строках а обозначает любую из цифр 8, 9, 0. Таким образом, здесь представлены все 24 возможности. Сделаем второй ход 1567. Ответ Об Ок оставляет выбор из трех неразгаданных чисел, для которых годится третий ход 8934 (табл. 6 б). При ответе 26 можно сыграть 1506 (табл. 6 в), а при ответе 1к - 5634 (табл. 6 г).

Таблица 6, в

Таблица 6, г

Для девяти чисел с ответом 16 в табл. 6 а составим табл. 6 д (вновь а может принимать одно из трех значений - 8, 9, 0). Третий ход 3564 разделяет их на три равные группы, четвертым ходом числа идентифицируются, и пятый ход завершит игру (ответ 4б). У нас осталось еще шесть чисел, расположенных в нижних строках табл. 6 а, выпишем их отдельно (табл. 6 е). И с этой шестеркой удается разобраться за два дополнительных хода. Итак, вновь партия длится не более пяти ходов.

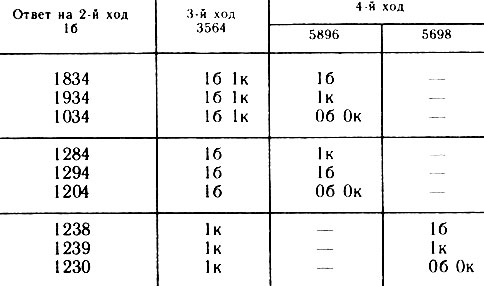
Таблица 6, д

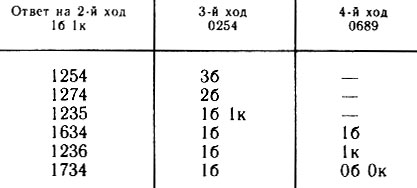
Таблица 6, е

Результаты всех рассмотренных партий собраны в табл. 7. Строгое доказательство того, что в каждом случае меньшим количеством ходов не обойтись, мы опускаем.

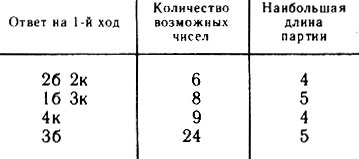
Таблица 7

Разобранные примеры показывают, что искусная игра в "быки и коровы" требует тонкого математического расчета.