106. Волшебная таблица

Вот таблица, в которой в пяти столбцах написаны известным образом все числа от 1 до 31. Таблица эта отличается следующим "волшебным свойством".

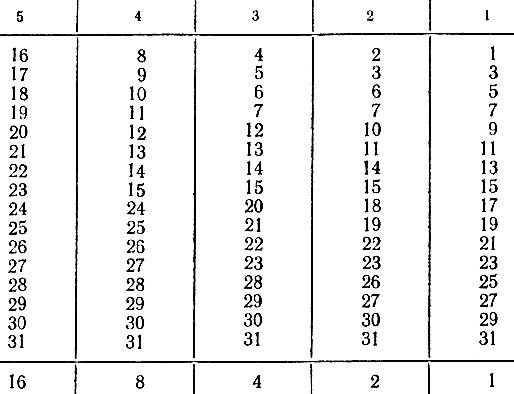
Задумайте какое угодно число (но, конечно, не больше 31) и укажите только, в каких столбцах этой таблицы находится задуманное вами число, а я тотчас же "угадаю" это число.

Если, например, вы задумаете число 27, то скажите только, что задуманное вами число находится в 1-м, 2-м, 4-м и 5-м столбцах; а я уже сам вам скажу, что вы задумали именно число 27. (Можно это сказать, даже не глядя на таблицу.)

Вместо такой таблицы можно смастерить

Волшебный веер. Сделайте сами или купите подходящий веел и на пяти пластинках его выпишите изображенную выше таблицу. Можете, обвевая себя веером, предлагать вашему собеседнику задумать число и указать вам только пластинки, на которых оно написано. Вы тотчас угадаете задуманное число. Но в чем секрет?

Решение. Секрет разгадывания с виду прост: обратите внимание на цифры, написанные в самой нижней графе. Если вам скажут, например, что задуманное число находится во 2-м, 3-м и 5-м столбцах, считая справа (или на 2-й, 3-й, 5-й пластинках веера), то сложите числа, стоящие в этих столбцах внизу, получите 22 (2 + 4 + 16), и будьте уверены, что задумано именно это, а не иное какое-нибудь число.

Еще пример - число 18. Вы найдете его во 2-м и 5-м столбцах. Внизу этих столбцов стоят числа 2 и 16; сложенные вместе, они дают действительно 18. Как же составляется подобная таблица?

Если написать ряд чисел, начиная с 1, таких, чтобы каждое было вдвое больше предыдущего, т. е. 1, 2, 4, 8, 16, 32, ..., то ряд этот обладает тем замечательным свойством, что каждое целое положительное число может быть получено, и не более чем одним способом, как сумма некоторых членов ряда. Например, 27 = 16 + 8 + 2 + 1. Для составления таблицы мы взяли только начальные члены ряда: 1, 2, 4, 8, 16 (2⁰, 2¹, 2², 2³, 2⁴), сложением которых можно получить все числа от 1 до 31 ( = 2⁵ - 1). За каждым из них закреплен определенный столбец таблицы (см. нижнюю строку). Воспользовавшись указанным выше свойством ряда степеней двойки, мы помещаем каждое целое число в те столбцы, в основании которых стоят степени двойки, в сумме составляющие это число. Так 27 попадает в столбцы с основаниями 1, 2, 8, 16. Теперь ясно, почему для угадывания достаточно сложить числа, стоящие внизу столбцов. Можно воспользоваться этим свойством степеней двойки для обозначения чисел. Напишем для каждого числа последовательность из 0 и 1 такую, что на первом месте справа стоит 1 или 0 в соответствии с тем, содержится наше число в первом столбце или нет, на втором 1 или 0 в зависимости от того, стоит ли число во втором столбце, и так далее. Например, число 27 обозначается этим способом так: 11011, а число 12 - так: 01100. Условимся не писать нули, стоящие слева, тогда для числа 12 получим представление 1100.

Такой способ записи называется двоичной системой изображения чисел.

Для того чтобы изобразить число с его помощью, совсем не обязательно иметь перед глазами таблицу. Достаточно представить целое число в виде суммы степеней двойки и на местах, номера которых (считая справа налево, начиная с 0) участвуют в этом представлении, поставить 1, а на остальных местах 0:

Двоичная система очень удобна для представления чисел в вычислительных машинах, так как для записи любого числа достаточно только двух знаков - 0 и 1. В общеупотребительной же десятичной системе для этого требуется 10 знаков - 0, 1, 2, ..., 8, 9.