VIII. Геометрические софизмы и парадоксы

95. Загадочное исчезновение

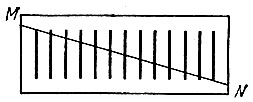
Рис. 103

Начертите на прямоугольном куске картона 13 одинаковых палочек на равном расстоянии друг от друга, так, как показано на рис. 103. Теперь разрежьте прямоугольник по прямой MN, проходящей через верхний конец первой палочки и через нижний конец последней. Если затем вы сдвинете обе половины так, как показано на рис. 104, то заметите любопытное явление: вместо 13 палочек перед вами окажется всего 12! Одна палочка исчезла бесследно. Куда же она девалась?

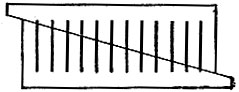
Рис. 104

Решение. Если вы сопоставите длины палочек на первом и втором рисунках, то обнаружите, что палочки на втором рисунке на ¹/₁₂ длиннее палочек первого рисунка. Исчезнувшая 13-я палочка улетучилась не бесследно: она словно растворилась в 12 остальных, удлинив каждую из них на ¹/₁₂ своей длины Геометрическую причину зтого понять очень легко Прямая MN и та прямая, которая проходит через верхние концы всех палочек, образуют угол, стороны которого пересечены рядом параллельных прямых. Из подобия треугольников следует, что прямая MN отсекает от второй палочки ¹/₁₂ ее длины, от третьей ²/₁₂, от четвертой ³/₁₂ и т. д. Когда же мы сдвигаем обе части картона, то приставляем отсеченный отрезок каждой палочки (начиная со второй) к нижней части предыдущей. А так как каждый отсеченный отрезок больше предыдущего на ¹/₁₂, то каждая палочка должна удлиниться на ¹/₁₂ своей длины. На глаз это удлинение незаметно, так что исчезновение 13-й палочки на первый взгляд представляется довольно загадочным.

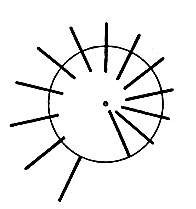
Рис. 105

Чтобы усилить эффект, можно расположить палочки по кругу, как показано на рис. 105. Если вырезать внутренний круг и укрепить его в центре так, чтобы он мог вращаться, то, повернув круг на небольшой угол, мы опять увидим, что одна палочка исчезла (рис. 106).

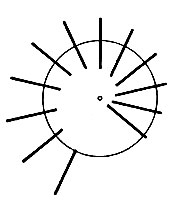
Рис. 106