91. Из квадрата - три квадрата

Разрезать квадрат на семь таких частей, чтобы, сложив их надлежащим образом, получить три равных квадрата.

Решение. Пусть ABCD (рис. 98) - данный квадрат. Отложим на его стороне отрезок DE, равный половине диагонали этого квадрата. Соединим А с Е и на полученную прямую АЕ опустим перпендикуляры DF и BG. Затем откладываем отрезки GH, GK, FL, все равные DF; заканчиваем построение прямыми, параллельными или перпендикулярными DF, как показано на рис. 98. Если разрезать теперь квадрат по проведенным линиям и сложить затем все полученные части так, как указано на рис. 99, то получим три искомых квадрата.

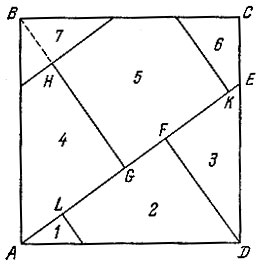
Рис. 98

Замечание. Математическое доказательство этого факта предоставляем читателю, заметив только, что, пользуясь подобием треугольников и теоремой Пифагора, доказанной в одной из предыдущих задач, нетрудно вывести, что 3|DF|²=|AB|².

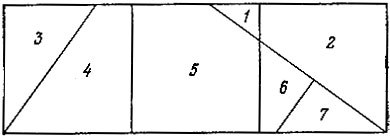
Рис. 99

Рассматриваемую задачу можно обобщить:

1. Разрезать квадрат на такие части, из которых можно было бы составить данное число равных квадратов.

2. Разрезать квадрат на наименьшее число частей, которые, соответственно сложенные, давали бы некоторое число равных между собою квадратов.