83. Теорема Пифагора

Показать, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

Рис. 79

Нарисуем два равных квадрата, стороны которых равны сумме обоих катетов данного на рис. 79 треугольника. Затем в полученных нами квадратах произведем построения, указанные на рис, 80, 81. Здесь от каждого из равных квадратов мы отнимаем по 4 равных треугольника. Если отнимать от равных величин поровну, то и остатки получатся равные. Эти остатки на рис. 80, 81 заштрихованы; но на рис. 80 получаются два квадрата, построенные на катетах данного треугольника, а на рис. 81 - квадрат, построенный на гипотенузе, и сумма площадей первых двух квадратов равна, следовательно, площади второго.

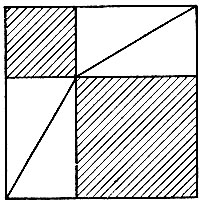
Рис. 80

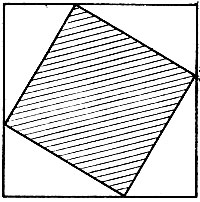
Рис. 81

Мы доказали, таким образом, знаменитую теорему Пифагора.

Другое доказательство той же знаменитой теоремы найдем, если на взятом бумажном квадрате сделаем сгибы, как указано на рис. 82.

Рис. 82

Здесь GEH есть прямоугольный треугольник и площадь квадрата, построенного на ЕН, равна сумме шющадей квадратов, построенных на EG и GH.