Эпидемии в свете чисел (Л. А. Рвачев, доктор физико-математических наук)

Эпидемии в свете чисел

В статье пойдет речь о математическом моделировании эпидемических процессов. Требования общественной безопасности давно уже указали на необходимость создания противоэпидемического щита. Он существует, однако в жизни мало заметен. Без него человечество по-прежнему потрясали бы эпидемии, причем еще более опустошительные, чем в средние века. Урбанизация и общественные коммуникации создают для их развития благоприятные условия. В этих условиях надежность защиты должна быть особенно эффективной, чтобы было возможно управлять течением эпидемии, сводя ее к минимуму.

Есть лишь один путь выявить количественный аспект законов развития эпидемии - моделирование. Экспериментальный путь исключается (вряд ли разумно вызывать эпидемии), а феноменологический мало реален (из-за трудностей количественного характера).

Уже более полувека успешно развивается математическая теория эпидемий, однако занимается она либо построением вероятностных моделей для вспышек в небольших коллективах, либо различными статистическими исследованиями, включая формальную аппроксиoмацию эпидемий, либо абстрактными моделями. Речи о моделировании конкретных больших эпидемий в математической теории эпидемий почти не было. Это наглядно показал организованный ВОЗ (Всемирной организацией здравоохранения) в ноябре 1970 г. Международный симпозиум по количественной эпидемиологии. На нем были представлены, по существу, все страны, занимающиеся теорией эпидемий: США, Англия, Франция, ФРГ, Япония, Канада и др. В докладах советских ученых были приведены результаты по моделированию почти 100 вспышек гриппа в крупнейших городах СССР.

Результаты этих работ (как доложенные на симпозиуме, так и новые) были получены из некоторой общей математической теории, идею которой коротко можно сформулировать так: коль скоро состояние больного (инфекционный процесс) в каждый момент времени зависит от двух чисел (уровень инфекции и уровень иммунитета), а эпидемия есть множество, элементами которого являются переменные состояния зараженных инфекцией людей, то нельзя ли интерпретировать эпидемический процесс как течение жидкости? С той, правда, разницей, что движение отдельных ее составляющих будет подчиняться не законам Ньютона, а инфекционному процессу, уравнения модели которого нужно еще написать.

Иначе говоря, мы обратились к возникшей еще в прошлом веке модели механики сплошных сред, или механики континуума. Математически это выражается в соединении в одном уравнении (уравнение непрерывности) противоположных понятий дискретной частицы и материального континуума. Эта модель применяется в самых различных задачах теоретической физики от гидродинамики до квантовой механики. Но хотя модель и общая, из-за специфики законов движения частиц каждый раз получается новая механика. Поэтому когда мы начали применять эту модель в эпидемиологии (изучая большую популяцию индивидуумов как поток в пространстве их состояний), то получили новый раздел механики сплошных сред, который, видимо, можно назвать "эпидемической механикой", или "эпидемической динамикой" (по аналогии, например, с "газовой динамикой").

Может создаться впечатление, что мы обязаны физике лишь уравнением непрерывности. В действительности же в каждой содержательной теории главное - не ее принципы или исходные уравнения, а тот круг понятий, в терминах которых ведется само изложение, ибо этим в конечном итоге определяются и аксиоматика и плодотворность данной теории. Механике сплошных сред мы обязаны гораздо большим, чем уравнениями; мы принимаем ее модель и средства языка, т. е. целый ряд представлений - плоские области, координаты, границы и граничные условия, траектории частиц, поля скоростей, потоки сплошной среды и многое другое. Именно эти языковые средства и стоящие за ними интуитивные представления делают последующую формализацию эпидемиологических представлений сравнительно простой и эффективной.

Ясно, что идею механики сплошных сред можно использовать для построения не только эпидемической динамики, но и единого подхода к широкому кругу медико-биологических и медико-социальных задач, где на основании исследования процессов в индивидуумах требуется получить представление о динамике соответствующей структуры населения или других популяций. В общем случае это означает исследование потоков в фазовом пространстве. Другое дело, что в настоящее время не для всех задач такой путь интересен. Так, например, применение механики сплошных сред к популяциям микромира может оказаться преждевременным, так как о динамике популяции в целом сейчас, видимо, судить легче, чем о законах динамики отдельных микроорганизмов.

Постараемся сформулировать в общем виде постановку такой задачи. Пусть в каждом индивидууме популяции Р протекает непрерывный медико-биологический процесс, для измерения которого приняты величины φ₁, φ₂, φ₃, ..., ..., φ_n. Их совокупность называется состоянием индивидуума. Пусть величина ф достаточна для детерминированного описания процесса, т. е. последующее состояние индивидуума предопределяется предыдущим:

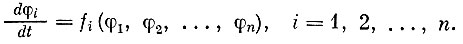(1)

Эти уравнения можно рассматривать как модель процесса в индивидууме. Будем называть их также уравнениями движения частицы. Вид функций f_i может быть самый различный и зависеть от конкретных задач. Отсутствие t в правых частях системы означает однородность времени по отношению к исследуемому процессу. Однако это не значит, что учитывается только стационарное влияние внешней среды на индивидуум. Структура f_i может содержать и влияние, меняющееся со временем, например лечение. Заметим, что не следует смешивать независимость функций f_i от времени с теми случаями, когда происходит массовое воздействие на популяцию, определяемое календарным временем, скажем, осуществление по графику каких-либо медико-биологических мероприятий. Подобная ситуация будет учитываться другими уравнениями, а уравнение (1), как мы уже говорили, относится к отдельному индивидууму. Пусть каждому индивидууму соответствует представляющая его частица, непрерывно движущаяся в фазовом пространстве (рис. 12). к Тогда система дает уравнения траектории отдельной частицы, а вектор, определенный правыми ее частями, - стационарное поле скоростей в пространстве для всего потока.

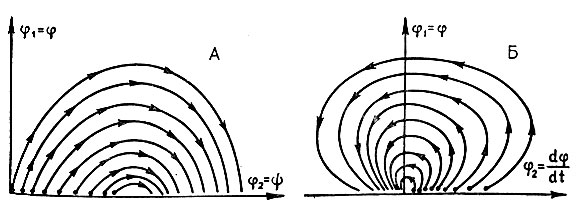
Рис. 12. Траектории потоков больных в фазовом пространстве

В большинстве задач требуется разбить полную популяцию на несколько частных, в зависимости от специфики индивидуумов или внешнего воздействия разных ареалов их пребывания и т. д. Тогда между потоками различных популяций в результате воздействия внешних сил может происходить обмен частицами, т. е. меняться структура уравнения (разумеется, частица при этом обмене остается в той же точке фазового пространства). В нормальных случаях связи между этими внешними силами и индивидуальностью конкретной частицы, совершающей переход между потоками, нет, следовательно, для частицы этот переход является случайным, происходящим с определенной вероятностью.

Таким образом, плотность распределения каждого потока будет описываться уравнениями непрерывности с модифицированной правой частью, представляющими собой общий вид модели для процесса в популяции. Будем называть их также уравнениями движения потоков, представляющих популяцию.

Теперь приступим к определению конкретного вида функций f_i. Рассмотрим, с одной стороны, механизмы размножения микроорганизмов и выработки антител, а с другой - случайный характер столкновения микрочастиц в системе лимфо-кровообращения и других жидких средах организма. В качестве первого приближения к инфекционному процессу получим уравнения относительно двух неизвестных функций времени (уровень инфекции и уровень защиты), которые также содержат: суммарную вероятность размножения и естественной гибели микроорганизма, вероятность гибели микроорганизма в результате столкновения с антителами, прирост защитных сил макроорганизма, вероятность нейтрализации антитела в результате столкновения с антигенами, вероятность спонтанного выключения элемента защитных сил организма. Эту последнюю вероятность мы будем полагать равной нулю, так как в конечном итоге нас будут интересовать лишь эпидемические процессы, а длительность эпидемических вспышек такова, что за этот период возникшие у организма иммунные силы не успевают сколько-нибудь заметно снизиться.

Хотя компоненты инфекционного процесса линейно зависят от своих причин, уравнения движения соответствующей частицы с самого начала получаются нелинейными. При подлинном моделировании иного результата и нельзя было ожидать, так как в медицине центральным местом инфекционного процесса считается взаимодействие антигенов и антител, которое имеет явно вероятностный характер.

Если осуществить описанное первое приближение, получается система двух нелинейных дифференциальных уравнений первого порядка. Эти уравнения называются каноническими.

Последние наиболее удобны при теоретическом исследовании проблемы - в силу своей простоты и наглядной связи с медицинскими представлениями. Однако I при исследовании конкретных случаев часто получается так, что эмпирической информации явно не хватает. С другой стороны, всякое эмпирическое описание инфекционного процесса медики обычно представляют в плохо формализуемых понятиях. Возникает вопрос: как проверять по эмпирическим данным рассмотренное выше движение в канонических координатах?

Для этой цели решим канонические уравнения (это возможно в неявном виде). Проведенное исследование показывает, что использование канонических координат можно подвергнуть количественной проверке по эмпирическим данным.

Таким образом, описание эпидпроцессов в терминах эпидемической динамики действительно может сопоставляться с эмпирической информацией об этих процессах.

Здесь нет возможности описать более подробно абстрактную эпидемическую динамику. Заметим лишь, что в конце концов появляются все данные для исследования реальных эпидемий.

Грипп сегодня - в некотором смысле исключительная инфекция. При эпидемиях гриппа механизм процесса настолько обнажен, а основные черты эпидемии проявляются так отчетливо, что практически без всякого изменения можно применять только что построенную модель. Объясняется это тем, что, во-первых, грипп очень контагиозен, во-вторых, его эпидемии имеют поистине глобальный характер и, в-третьих, имеющиеся средства профилактики и лечения до настоящего времени еще не могут считаться Достаточно эффективными. Иначе говоря, распространение этой инфекции все еще происходит на основе ее естественных закономерностей.

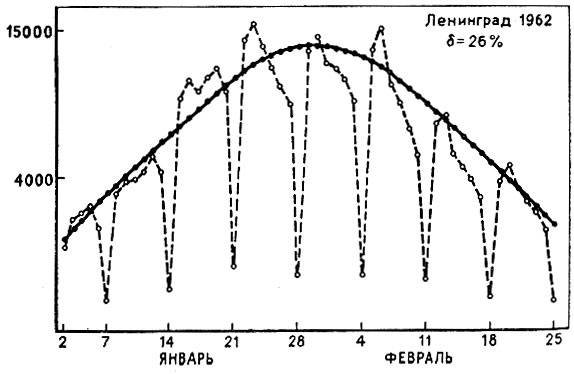
Рис. 13. Моделирование без учета недельных циклов

Актуальность моделирования эпидемий гриппа обусловлена их масштабами. Так, в СССР заболеваемость при эпидемии довольно высока и приводит к экономическим Потерям. За периоды пандемий гриппа переболевает почти треть человечества, причем наибольший экономический ущерб наносится развитым странам.

Информация, которую мы приведем, будет более обширной, чем такая же информация относительно других эпидемических процессов. Только отчасти это объясняется тем, что модель гриппа - более разработанная. Главное: грипп представляет наиболее удобный объект исследования. На его примере нагляднее всего можно увидеть научные и практические цели моделирования эпидемий вообще.

Хотя эпидемия гриппа представляет собой многофакторный естественносоциальный процесс, существует лишь единственное, доступное полному и точному наблюдению в общегородском и тем более в общенациональном масштабе его проявление - официально регистрируемая заболеваемость. Другие возможные статистические материалы либо не очень надежны и крайне неполны, либо просто отсутствуют. Следует подчеркнуть, что этот аспект является самым важным и для здравоохранения, поскольку ущерб от эпидемий гриппа связан почти всецело с их социально-экономическими последствиями, т. е. с временной потерей трудоспособности населением.

Таким образом, складывается ситуация, которая на первый взгляд подрывает саму идею моделирования эпидемий гриппа. В самом деле, во-первых, в качестве мае-?совой информации мы можем располагать только официально регистрируемой заболеваемостью, во-вторых, известно, что официально регистрируемая заболеваемость р.и фактическая заболеваемость существенно отличаются, так как далеко не все больные обращаются к врачу; наконец, в-третьих, уравнения модели по своему смыслу ?фебуют учета именно фактической заболеваемости, болee того - ее численного выражения.

Затруднения преодолеваются принятием следующего постулата: в каждый момент времени в множестве вновь заразившихся лиц, которым предстоит лечение, к врачу будет обращаться одна и та же их доля. Этот постулат не противоречит здравому смыслу и данным некоторых социологических исследований, касающихся статистики вызова врача на дом.

Теперь, хотя мы и не собирались останавливаться на технических деталях, затронем вопрос об обработке этой ?информации. При анализе колебаний эпидемий гриппа (волн) видно, что для каждого города внутри общей тенденции эпидпроцесса имеется еще и ярко выраженная сильная периодичность. Между тем ясно, что реальная на не регистрируемая заболеваемость (коль скоро мы имеем дело с большой эпидемией) как функция времени должна иметь гладкий характер. Причина этих недельных циклов заключается в чисто психологическом, давно известном эпидемиологам факторе: перед выходными днями население менее охотно обращается к врачу, а после обращаются все, в том числе и многие их тех, кто заболел накануне. Мы выдвинули предположение, что каждый день недели имеет свою более или менее стабильную вероятность обращения к врачу при условии заболевания. Для его проверки были по реальным данным вычислены поправочные коэффициенты, зависящие от номера дня недели и не зависящие от времени, места, т. е. города и времени года (существенные отклонения наблюдались лишь перед праздниками).

Учет этих коэффициентов при моделировании осуществлялся (конечно, только при машинной выдаче результатов) путем дополнительного умножения расчетной заболеваемости за некоторый день на коэффициент этого дня. Забегая несколько вперед, можно продемонстрировать эффективность моделирования без коэффициентов (рис. 13, пунктир - реальные данные, сплошная линия - расчетные) и с коэффициентами (рис. 14). Среднеквадратичное уклонение расчетной кривой от реальной в первом случае составляет 26%, а во втором - 5%.

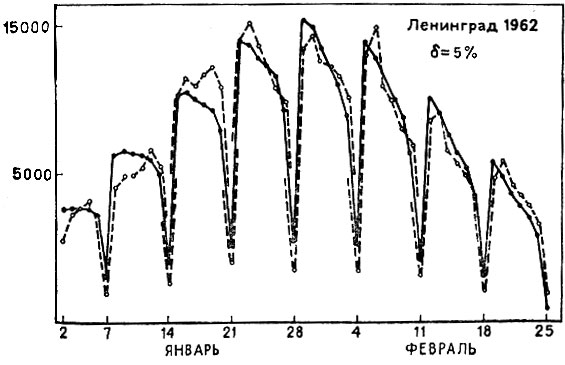
Рис. 14. Моделирование с учетом недельных циклов

Однако чтобы модель можно было проиграть на ЭВМ, учета только этих коэффициентов недостаточно. Нужно научиться определять параметры, характеризующие кон-тагиозность инфекции, начальную иммунную структуру населения и, кроме того, социальную индивидуальность ареала, где протекает эпидемия (к примеру, город). Определение этих параметров путем прямых наблюдений или статистических исследований представляется практически невозможным. Поэтому нами был использован окольный путь - анализ волн эпидемических кривых заболеваемости.

Нами были промоделированы все представленные статистические материалы, а именно: данные о 169 вспышках гриппа в 43 крупнейших городах СССР по всем эпидемиям за последние 15 лет. И первый результат, который при этом получился, были 169 пар оптимальных значений искомых параметров. Второй результат приведен в виде примеров на рис. 15 и 16. Речь идет о сравнении реальных кривых ежедневной заболеваемости (пунктир) и соответствующих машинных кривых (сплошная линия). Другие обозначения на рисунках: СР - реальная сумма переболевших в городе за период вспышки, СМ - машинная сумма переболевших в городе за тот же период.

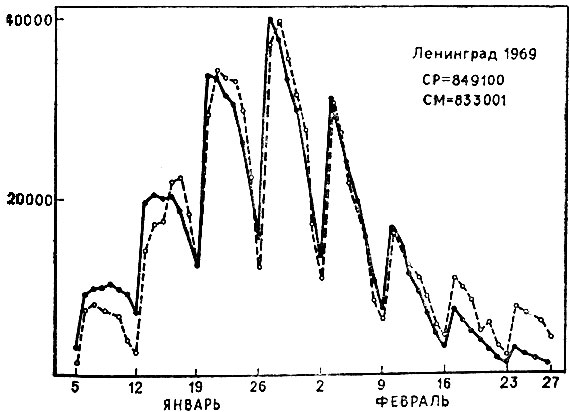
Рис . 15. Пример использования локальной модели

Эти результаты позволяют оценить надежность модели. Обращает на себя внимание высокая стабильность результатов. Если вспомнить, что речь идет о таких объектах, как эпидемия (а это - вероятностный процесс), можно вделать следующий принципиальный вывод: для эпидемий гриппа нет особого смысла стремиться к улучшению средств моделирования как таковых, нужно стремиться к всестороннему улучшению вводимой в модель информации. (Тем более, что структура модели в значительной степени адекватна природе исследуемых процессов.)

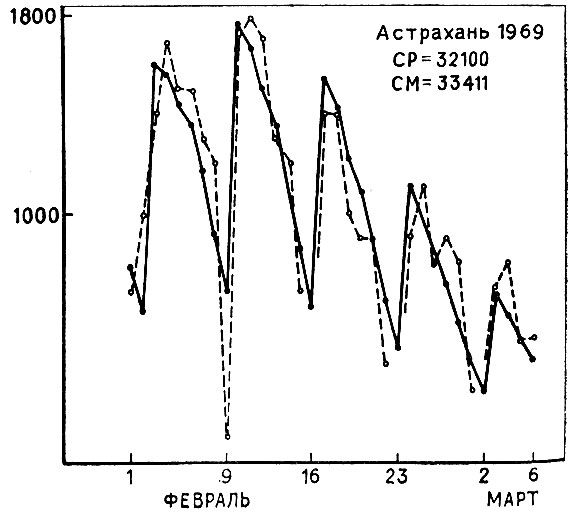
Рис. 16. Пример использования локальной модели

Таким образом, надежность локальной модели установлена. Это позволяет решать некоторый класс задач, которые никакими другими путями решены быть не могут. Речь идет о том, что по сравнению с большинством естественнонаучных дисциплин эпидемиология, как мы об этом уже говорили, находится в невыгодном положении - она не может пользоваться экспериментом. В этом отношении эпидемиолога можно сравнить с астрономом. С той, правда, разницей, что в отличие от астрономов эпидемиологи не могут вполне воспользоваться и феноменологическим методом. Эпидемии не столь повседневны, чтобы в одинаковых условиях можно было наблюдать целую их серию, достаточную для установления численных закономерностей. Сравнивая две большие эпидемии, происшедшие в разном месте или времени, мы обычно видим, что различие затрагивает не один, а многие параметры, начиная от экологических условий и кончая, быть может, изменчивостью патогенного агента.

Легко видеть, что ситуация в корне меняется, когда эпидпроцесс большого масштаба вместе с популяцией, в которой он протекает, удается моделировать достаточно эффективным образом. Ведь с моделью можно производить какие угодно эксперименты, и притом с большим ускорением. Так, 3-месячный эпидпроцесс для всей территории СССР в машине БЭСМ-6 протекает около 2 мин.

Забегая несколько вперед, приведем пример использования союзной модели. По заказу Министерства путей сообщения СССР была исследована задача о том, как влияет интенсивность пассажирооборота в транспортной сети страны на масштабы общесоюзной эпидемии гриппа. Результаты решения приведены на рис. 17 и 18. (По горизонтали - время в днях, по вертикали - ежедневная заболеваемость по 100 крупнейшим городам нашей страны). Из рисунков видно, что, с одной стороны, мероприятия по уменьшению циркуляции больных в межгородской сети практически бесполезны, а с другой, в связи с ростом интенсивности пассажирооборота - масштаб будущих эпидемий заметно не увеличивается.

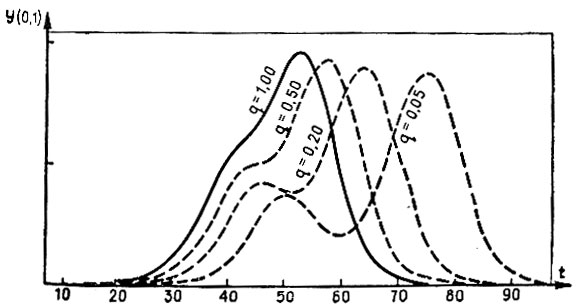
Рис. 17. Изменение союзного эпидпроцесса при уменьшении количества больных в транспортной сети СССР

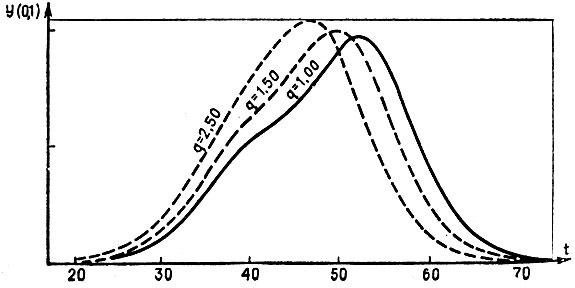
Рис. 18. Изменение союзного эпидпроцесса при увеличении интенсивности транспортной сети СССР

Теперь расскажем, как была построена модель для территории СССР. Мы выбрали 100 городов с наибольшим населением. (По данным на 1970 г., это оказались почти все города с населением свыше 100 тыс. человек.) Возник вопрос, не оказывает ли эпидемия, протекающая на остальной территории, где проживают десятки миллионов людей, заметное обратное влияние. Так как априори тут ничего сказать было нельзя, то мы решили осуществить моделирование и для остальной части страны, но лишь очень приблизительно. С этой целью территория страны, за исключением малонаселенных районов, была разбита на 28 зон, которые примерно соответствовали основным экономическим районам СССР. Эти зоны образовали дополнительные элементы модели со своими индексами и коэффициентами. Разумеется, из каждой такой зоны устранялся город, включенный в систему 100 городов. В результате модель охватила территорию, на которой проживает примерно 98 % населения страны. Внутри каждой зоны эпидемия рассчитывалась по уравнениям для городов, что, конечно, не способствовало точности расчетов. Но это было несущественно, так как во всех известных нам случаях эпидемия распространялась из больших городов в воны, а не наоборот, т. е. зоны, промежуточные в географическом отношении, не были промежуточными в плане передачи инфекции. (Инфекция передавалась непосредственно поездами и самолетами.) Географическая структура модели для территории СССР стала включать 128 элементов - городов и зон, связанных ежедневным пассажирооборотом.

Построенная таким образом модель для территории государства обладает одним новым (сравнительно с локальной моделью) существенным свойством: она может прогнозировать численный ход эпидемии.

Настоящий раздел уместно начать с небольшого экскурса в историю. В 1966 г. мы начали применять в эпидемиологии интуитивные представления механики сплошных сред. Сначала была построена чисто теоретическая модель эпидемии гриппа (как это делалось, описано в предыдущем разделе). Статистические материалы, которыми мы располагали, были только по вспышке гриппа 1965 г. в Москве. Правда, мы имели еще ориентировочное представление о заболеваемости в первые дни января 1965 г. в Ленинграде (когда там начиналась вспышка). Причем знали, что Ленинград был исходным городом, т. е. сюда эпидемия пришла из-за границы и отсюда распространилась на всю страну. Московские данные были воспользованы для определения параметров, а ленинградские - как начальное состояние систем. Эпидемический Кфоцесс был рассчитан для всех 128 городов, и для Москвы шюлучилось совпадение с реальными данными, что доказывало: эпидемии гриппа на больших территориях в принципе моделируемы. Однако, кроме Москвы, сравнивать было не с чем, да мы к этому и не стремились, так как не было оснований полагать, что такое сопоставление приведет к чему-нибудь хорошему. Кроме того, мы понимали, щто любая аппроксимирующая формула представляет еобой очень сомнительную замену для реального пасса-зкирооборота страны (с эпидемией 1965 г. нам просто довезло, так как указанная аппроксимация, как мы теперь знаем, для моделирования эпидемий пригодна лишь тогда, когда исходный город - мощный транспортный узел - такой, как Москва или Ленинград). В силу этих соображений нам казалось, что основной областью применения союзной модели должно быть установление численных закономерностей эпидемических процессов. К идее же прогнозирования относились скептически, полагая, что здесь нужен чрезмерно большой объем социально-медицинской информации. Однако когда в 1970 г. из горздравотделов городов страны к нам начали поступать массовые статистические материалы по ежедневной заболеваемости в периоды различных эпидемий, то сотрудники лаборатории сопоставляли эти материалы с указанной машинной выдачей по эпидемии 1965 г. Результаты сопоставления явились для нас своего рода сенсацией, так как "только для 4 городов из 23 прогноз можно было считать неудовлетворительным. Таким образом, оказалось, что модель способна прогнозировать, а расчет эпидемии 1965 г. являлся чистым прогнозом, поскольку, делая его, мы понятия не имели о реальных данных, которые собирались прогнозировать. Получили мы их лишь 4 года спустя.

Рассмотрим теперь уровень прогнозирования, достигнутый на сегодняшний день. Под прогнозом понимается введение в машину данных только за период подъема заболеваемости в исходном городе и последующую выдачу ежедневной заболеваемости по остальным городам системы по уравнениям модели для территории страны на период предстоящей союзной эпидемии. Первоначально предполагалось, что определенные по исходному городу свободные параметры дадут нам только эпидемиологическую индивидуальность данной эпидемии и затем мы будем использовать дополнительные данные, характеризуй ющие социальные особенности различных городов. Однако мы пока что не располагаем такими коэффициентами, так что индивидуальность каждого города проявляется у нас лишь в численности населения и в его транспортных связях. Далее, по некоторому алгоритму, мы определяем искомую пару свободных параметров так, чтобы среднеквадратичное уклонение расчетной полуволны исходного города от его же реальной полуволны было минимальным. Но здесь нужно подчеркнуть некоторое, хотя и техническое, однако принципиально важное обстоятельство. Дело в том, что значения свободных параметров существенны не только для расчета величины эпидемических волн, но и их места на оси времени.

К этому можно добавить еще некоторые эвристические соображения по поводу одного из двух свободных параметров - иммунологической структуры населения. Этиологией возбудителя вспышки мы не занимаемся - это задача эпидемиологической интерпретации - для модели важны лишь численные значения соответствующих параметров. Но с формально-расчетной точки зрения мы вправе рассуждать так: раз на обширной территории, где на протяжении 2-3 лет наблюдался лишь фон заболеваемости ОРЗ, внезапно и практически одновременно (в течение нескольких месяцев) имеет место массовая заболеваемость, во много раз превосходящая фон, и эта заболеваемость имеет ярко выраженный инфекционный характер, то все это может свидетельствовать лишь о том, что появился инфицирующий "фактор X", который мы условно называем гриппом и который был не знаком для всей данной территории на протяжении по крайней мере последних лет (речь идет не обязательно о новом штамме, но, может быть, о каких-то сдвигах внутри штамма). Из подобной новизны "фактора X" следует, что по отношению к нему все районы территории в иммунологическом плане до начала вспышки в среднем были равноправными. Действительно, все те эпидемии, которые мы моделируем, были занесены в нашу страну извне, так что "фактор X" возникал первоначально где-то, например в Юго-Восточной Азии. Поэтому если бы какой-то район оказался иммунологически выделенным (по сравнению с другими) до начала союзной эпидемии, то это означало бы наличие корреляции между этим районом и "фактором X" еще до начала эпидемии, что противоречит тезису о заносе извне. При этом нас не должно смущать, что несмотря на новизну "фактора X" исследуемая территория может содержать значительный процент людей, не восприимчивых к этому фактору. Такой иммунитет естествен, так как в лице "фактора X" мы имеем дело лишь с вариацией внутри штамма, или вида. И поскольку не бывает идеально специфического иммунитета, то определенная доля лиц, приобретавших иммунитет к старым вариациям, попутно получила иммунитет и к новой вариации, хотя и не сталкивалась с ней. Важно лишь то, что начальный иммунитет есть случайная величина, не зависящая от "фактора Х". Таким образом, из всего этого можно также сделать вывод о приемлемости единого для всех городов значения иммунологической структуры населения.

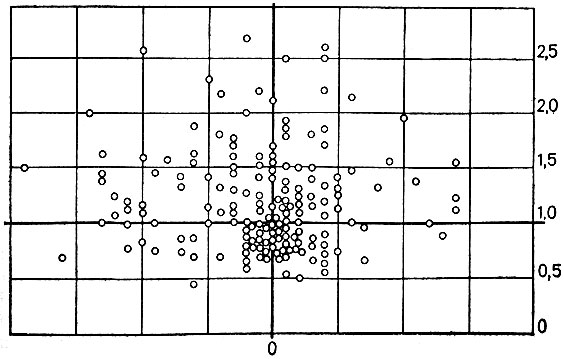
Рис. 19. Итоги прогнозирования суммарно по эпидемиям 1957, 1959, 1962, 1967, 1969, 1970 (приведено 170 вспышек в городах СССР)

Рассмотрим теперь проблему задания начальных условий для уравнений модели. В частности, для этого нужно выбрать начальный момент времени, т. е. принять некоторый календарный день за нулевой. Поскольку для расчета эпидпроцесса мы используем данные о ежедневной заболеваемости в исходном городе до пика включительно, казалось бы, естественно начинать счет с прогностической точки (прогностической точкой мы называем момент пика в исходном городе). Однако это приводит к существенной ошибке (к сдвигам эпидемических волн по времени) в силу следующих обстоятельств. Из-за отсутствия раздельной (и тем более точной) диагностики гриппозные вспышки численно обнаруживаются лишь тогда, когда заболеваемость начинает заметно превышать уровень фона. Поэтому для всех городов, кроме исходного, в прогностический момент мы будем вынуждены задавать либо какие-то заведомо произвольные ненулевые начальные данные, либо (для большинства городов) нулевые начальные данные. Это неверно, так как там не может не идти в этот момент процесс (ведь в исходном городе уже достигнут пик). И столь большая заболеваемость уже в течение ряда дней должна была рассеиваться через транспортную сеть по остальным городам. Таким образом, нужен специальный алгоритм, хотя и при этом отсутствие точной диагностики чрезвычайно усложняет определение начальных данных.

Нами был принят алгоритм, по которому счет начинался в тот момент, когда в транспортной сети впервые начинает циркулировать первый заболевший индивидуум. Для этого по расчетной кривой исходного города сначала рассчитываются плавные эпидпроцессы во всех тех городах, где к моменту прогностической точки уровень заболеваемости заметно превышает уровень фона. Назовем эти города начальными. Расчет эпидпроцесса в начальном городе осуществляется в два этапа: сначала определяется его высота, а затем - место на оси времени. Для размещения расчетной вспышки на оси реального времени ориентиром обычно служит прогностическая точка, так как если в этот момент заболеваемость заметно превышает уровень фона, то, считая волну относительной заболеваемости (относительно населения города) в начальном и исходном городе примерно одинаковой, можно определить, насколько сдвинута реальная эпидволна в начальном городе относительно реальной волны исходного. Следовательно, расчетная эпидволна в начальном городе должна иметь такой же сдвиг и относительно расчетной волны исходного города.

Полученная расчетная заболеваемость в начальных городах сопоставляется с величиной тех транспортных связей, которые исходят из начальных городов в любые другие (включая начальные). Для каждого начального города легко определить день, когда его расчетная заболеваемость впервые достигает уровня, при котором в наибольшую транспортную связь этого города ежедневно "излучается" один заболевший. Первый из этих дней (по всем начальным городам) мы и принимаем за начальный момент. Для него задаются во все начальные города ненулевые начальные данные, в качестве которых берем уже имеющуюся у нас расчетную заболеваемость в день начала счета и предшествующие 5 дней. Во все остальные города системы задаются нулевые начальные данные. Разумеется, любую более раннюю дату также можно принять за начальный момент, а для определения начальных данных отступить соответственно назад - по расчетным кривым начальных городов.

Таким образом, с этого момента в некоторые города будет заноситься заметное количество больных. Следовательно, к моменту прогностической точки в городах, не являющихся начальными, уже автоматически возникает заболеваемость, вызванная начальными городами (по реальным данным мы не смогли бы ее определить, так как она сливается с фоном).

Разумеется, если в отдельных конкретных случаях есть возможность более простого определения начального состояния системы, то нужно этим воспользоваться. Вообще при прогнозировании допустимы любые манипуляции с любыми статистическими данными, лишь бы они были до прогностической точки и имели методически единообразный характер.

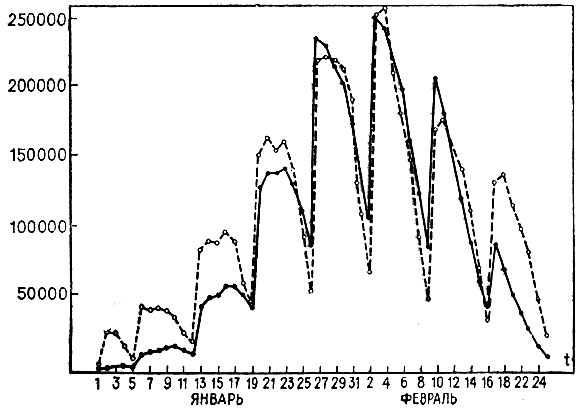
Рис. 20. Эпидемии 1969 г. Прогноз суммарной заболеваемости по 40 крупнейшим городам СССР

Прогностические свойства модели апробировались на материалах 170 вспышек гриппа в городах СССР по всем эпидемиям, начиная с 1957 г.

Мы рассмотрели методы прогнозирования. Рассмотрим теперь методы оценки его результатов. Здесь нужно руководствоваться несколько иными критериями, чем при оценке эффективности локального моделирования. Действительно, оценивая эффективность моделирования, нужно было доказать, что процесс в машине в определенной степени адекватен реальному эпидпроцессу. Следовательно, нужно было сопоставлять ход кривых в каждой точке времени. И среднеквадратичное уклонение являлось естественной мерой при таком сопоставлении.

Прогнозирование не предназначено для практического использования в здравоохранении, где прежде всего желательно предвидеть масштабы эпидемии по городам и время ее начала, планирование распределения сил и средств. Поэтому для оценки эффективности прогнозирования необходимо прежде всего сопоставлять расчетные и реальные эпидемические процессы, определить, с какой вероятностью и в каких пределах мы умеем предсказывать высоту и время пика вспышек в городах.

Вместе с тем здесь уместно напомнить, что речь не идет о прогнозировании в том смысле, чтобы предугадать заранее, будет в стране эпидемия или нет (это умеют делать, пo-видимому, только медики, и притом далеко не всегда). А модель могла бы определять это только для пандемий, Щи только в том случае, если бы была расширена до глобальной. Прогнозирование в модели для СССР становится ?возможным лишь в тот момент, когда хотя бы в одном городе уже происходит подлинная вспышка. Только после этого модель в состоянии прогнозировать количественную динамику процесса в стране.

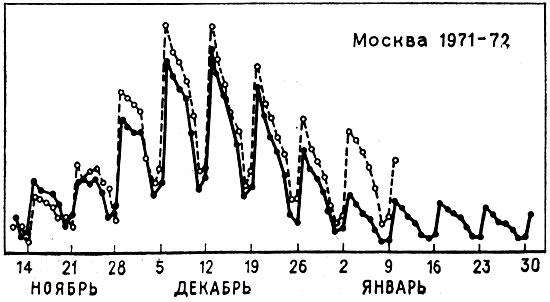
Рис. 21. Прогяозирование по критерию 'в' в плане предсказания ежедневной заболеваемости по городу

Результаты прогнозирования оценивались по трем критериям:

• Предсказание для городов одновременно дня пика вспышки и его высоты. Здесь мы называем прогнозом, хорошим во всех отношениях, тот случай, когда момент пика данного города предсказан с точностью до 5 дней, а высота пика этого же города - с ошибкой менее полуторакратной.
• Предсказание для городов только момента пика вспышки (наиболее важный фактор для эпидемиологов), где удовлетворительным мы считаем предсказание с точностью до недели.
• Сопоставление реальных и прогностических эпидкри-Ввых ежедневной заболеваемости как для городов в отдельности, так и суммарно по СССР.

Результаты прогнозирования по критериям "а" и Веб": удовлетворительный прогноз моментов вспышек был достигнут в 80% всех случаев, хороший прогноз одновременно моментов и высот вспышек - в 54% всех случаев^*. Детально эти результаты изображены в виде "эллипса рассеивания" на рис. 19, где каждый кружок означает конкретную вспышку в конкретном городе. Координаты этого кружка имеют следующий смысл: горизонтальная координата означает сдвиг в днях предсказанного момента пика относительно реального, а вертикальная - отношение предсказанной высоты пика к реальной. Таким образом, при идеальном прогнозе все кружки слились бы в один с координатами (0,1) на пересечении двух выделенных на рисунке прямых, каждая из которых означает также идеальный прогноз, но только либо по высоте, либо по моменту пика.

^* (Любопытно, что когда модель стала применяться в практике Минздрава СССР, то прогноз оказался лучше, чем при указанной I апробации - 85 и 75% соответственно.)

Пример прогнозирования по критерию "в" в плане предсказания ежедневной заболеваемости суммарно по городам приводится на рис. 20. Характер же машинного прогноза для отдельных городов оюжно представить себе по примеру на рис. 21.

Из сказанного видно, что массовые испытания модели эпидемий гриппа для территории СССР в целом привели к вполне удовлетворительным результатам. Поэтому в сентябре 1971 г. модель была передана в Министерство Здравоохранения СССР для практического использования, а всего лишь через два месяца она подверглась испытанию самой жизнью: началась эпидемия гриппа. В начале декабря 1971 г. модель выдала прогноз ежедневной заболеваемости гриппом в 100 крупнейших городах СССР на период предстоящей эпидемии 1971-1972 гг. В марте 1972 г. можно было оценить, насколько успешным явился данный прогноз. По оценке Всесоюзного центра, по гриппу прогноз оказался вполне успешным в 75% всех случаев, а в 85% случаев была правильно предсказана неделя пика вспышки.

Аналогичный прогноз был дан и в эпидемиях 1973 и 1975 гг.

Эти результаты по прогнозированию служат одновременно и завершением проверки надежности союзной модели. Дело в том, что была подвергнута массовым испытаниям лишь локальная компонента союзной модели. Для оценки моделирования транспортной сети лучшим критерием является то, насколько успешно модельная транспортная сеть в состоянии обусловливать времена вешек в различных городах. Следовательно, указанные 80% попадания вспышек в предсказанный недельный интервал свидетельствует об удовлетворительном уровне моделирования транспортной сети. Таким образом, не только локальная, но и союзная модель пригодна для осуществления на ЭВМ различных эпидемиологических экспериментов.

Из всего сказанного, по-видимому, следует, что эпидемии гриппа можно прогнозировать с удовлетворительной точностью для территории любого развитого государства или относительно замкнутого региона. Такой вывод представляется естественным в силу того, что прогнозирование осуществлялось нами для территории столь обширной и разнообразной по экологическим условиям страны, как СССР.