Применение теории катастроф в психологии и экономике (А. В. Чернавский, доктор физико-математических наук)

Применение теории катастроф в психологии и экономике

Математические применения, о которых пойдет речь в этой статье, находятся в рамках нового подхода к описанию, прежде всего качественному, разнообразных явлений физических, биологических, социальных и прочих, который был развит в последние два десятилетия рядом математиков и получил название "теория катастроф". Цель статьи - дать сначала более или менее популярный обзор математических идей, стоящих за этим подходом, и затем рассказать о нескольких работах, в которых были сделаны первые шаги на пути применения этого подхода в области психологии и экономики. Разумеется, дело специалистов дать окончательную оценку и найти этим методам надлежащее место в своей науке. Однако следует иметь в виду, что за этими методами стоит много тонкой и нетрадиционной математики, и окончательное суждение может быть внесено только после длительных и благожелательных контактов специалистов с математиками.

Общая теория этого подхода, в сущности, совпадает oс классической теорией бифуркаций динамических систем. Однако придумавший новое название французский математик Рене Том [2] на основе фундаментальных идей X. Уитни [1] высказал ряд новых соображений, которые привели к существенному математическому развитию (Б. Мальгранж, Дж. Мезер, В. И. Арнольд) [3], и начал систематический анализ возможностей приложения этих идей в традиционно далеких от математики областях, главным образом в биологии. Наиболее развилась часть теории катастроф, называемая элементарной. В ее приложении (более прозрачном, чем общая идеология Р. Тома) большую роль играет английский тополот 3. Зиман, о работах которого мы будем рассказывать.

Математическую схему, в которую укладываются применения теории катастроф, можно представить следующим образом. Рассматривается динамическая система, то есть система обыкновенных дифференциальных уравнений первого порядка, разрешенная относительно производных, правые части которой зависят от параметров:

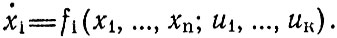
Фазовый портрет системы (то есть картина расположения интегральных кривых в пространстве Ox₁,..., х_n, называемом фазовой плоскостью) меняется при изменении параметров u_j. При этом возможен более простой случай, когда область изменения параметров в пространстве 0u₁,..., u_k можно разбить гиперповерхностями на ряд областей в конечном числе, так что в пределах каждой области картина качественно остается одной и той же, а при переходах через разделяющие гиперповерхности меняется скачками. (Слова "качественно одинаковые" имеют точный математический смысл, означающий, что имеется взаимно однозначное того или иного типа преобразование фазовой плоскости, переводящее одну картину в другую.) Принимается, что для параметров в пределах каждой области форма явления, описываемого системой, остается постоянной и резко меняется при переходах из одной области в другую. Эти резкие переходы можно назвать "сменой фаз". Область параметров, разделенная указанными гиперповерхностями, называется бифуркационной диаграммой. Вместе с качественным описанием системы в каждой ячейке и изменений при переходе из одной ячейки в соседние она дает требуемое описание явления.

На самом деле встречается (и является наиболее интересным) случай, когда резкий скачок при переходе через границу между фазами в зависимости от предыстории (конкретной траектории) происходит или не происходит. Разумеется, возможны случаи как в математике, так и в реальности, когда существенные изменения происходят непрерывно. Однако к описанному простому случаю относится важный частный случай так называемых градиентных динамических систем. Этот частный случай, к более подробному описанию которого мы переходим, и составляет элементарную теорию катастроф.

В дальнейших наших рассуждениях будем предполагать, что движение в фазовой плоскости совершается по градиентным линиям некоторой функции против градиента, то есть к минимуму. В векторной форме это записывается так: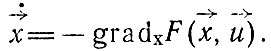

Будем также считать, что это движение быстрое (точка быстрее по сравнению с изменениями параметров достигает минимума или седловой точки и останавливается там). Тогда для каждого значения параметра нам важно отметить в фазовой плоскости точки минимума функции 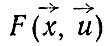. Отметим все стационарные точки (минимумы, максимумы, седла и вырожденные особые точки) и заметим, что в типичном случае их конечное число. Главное для нас состоит в том, чтобы проследить за характером их изменения при изменении параметров. Вообще говоря, они меняются непрерывно, но в отдельные моменты могут исчезать или появляться, причем, как правило, парами. Отмечая соответствующие значения O 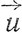параметров, мы и вычертим в области Ои бифуркационную диаграмму. Слова "вообще говоря" и "как правило" расшифровываются математически так: точки, вблизи которых стационарные точки функции F меняются непрерывно и число их не меняется, образуют в пространстве параметров ряд областей - "фаз"; поверхность, разделяющая две такие области, составлена из точек, где при переходе через нее из одной области в другую исчезает или появляется одна пара стационарных точек, которые при этом сливаются над самой поверхностью. Наконец, точки, где происходит слияние большего количества стационарных точек, образуют множество меньшей размерности, по которому сливаются разделяющие гиперповерхности. Важно заметить, что над каждой ячейкой би-фуркационной диаграммы лежит определенное число стационарных точек, которые при непрерывном изменении параметра описывают соответствующее число листов поверхности, пара из которых склеивается над каждой граничной поверхностью ячейки, а остальные переходят через нее в листы такой же поверхности над соседней ячейкой (или, наоборот, все листы переходят через границу и появляются два новых).

Простейший случай показан на рис. 13, где в качестве функции F взята функция х³+ux; пространства Ох и Оu одномерны; ниже показана упомянутая поверхность (это парабола 3х² = -u), состоящая из двух листов для отрицательных значений и и исчезающая для положительных. Таким образом, имеются две ячейки, разделенные нулем.

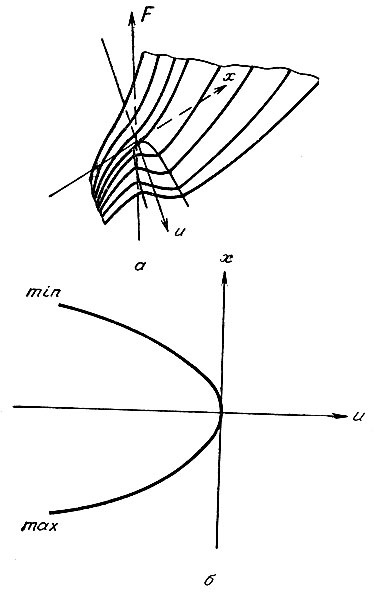
Рис. 13

В типичном случае разложение Тейлора функции F по переменным х в стационарных точках начинается с невырожденной квадратичной формы (положительно определенной в интересующих нас случаях минимума). В точках, лежащих над пограничными точками, разложение начинается либо с вырожденной квадратичной формы, либо со степеней, больших двух. В приведенном нами простейшем случае только в нуле разложение начинается (и кончается) членом х³. В остальных точках разложение в критических точках 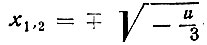начинается с квадратичного члена 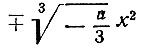(проверьте!) Рассмотрим теперь поведение динамической системы, отвечающей этому простейшему случаю. Считая, что параметр медленно (по сравнению с х) меняется от - 1 до +1, мы получим, что представляющая точка будет скользить по верхней ветви параболы (нижняя отвечает точкам максимума) и в момент перехода через нуль "сорвется" и уйдет в минус бесконечность. Чтобы продемонстрировать реальность этой картины, рассмотрим следующую модель, предложенную Т. Портосом (рис. 14).

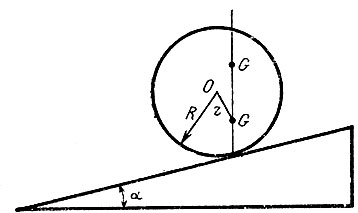
Рис. 14

Пусть на невесомом диске укреплен груз G на расстоянии r от центра. Сам диск катится вертикально по наклонной плоскости. Имеется два положения равновесия (над точкой касания), одно из которых устойчиво, а другое нет. Функция F в данном случае есть потенциальная энергия земного притяжения к Земле, роль параметра и играет r-Rsin α, где R - радиус диска, а α - угол наклонной плоскости к горизонту. При r = Rsin α оба положения равновесия совпадают, и при дальнейшем уменьшении u они исчезают и диск катится вниз.

Важный момент нашей математической схемы состоит в том, что в целом ряде случаев (к ним принадлежит элементарная теория катастроф) для переходных форм можно указать необходимое число параметров, которое оказывается конечным, чтобы описать все типичные перестройки системы, совершающиеся устойчиво при малом изменении параметров. Устойчивость означает, что малое возмущение самой перестройки не меняет ее характера. Чтобы понять это утверждение, рассмотрим бифуркационную диаграмму некоторого устойчивого (явления. Ясно, что для того, чтобы описать поведение, системы вблизи точки, лежащей на границе двух ячеек, достаточно потратить один параметр, а именно: достаточно проследить за поведением системы вдоль кривой, идущей из одной ячейки в другую через нашу точку. Если же мы возьмем точку, лежащую на стыке нескольких граничных поверхностей, то почти для всех таких точек потребуются два параметра (нужно рассмотреть кусок двухмерной поверхности, пересекающей в данной точке многообразие стыка, которое, например, в трехмерном пространстве будет кривой, а вообще будет на две размерности меньше, чем все пространство). Затем останется некоторое меньшее множество, для точек которого потребуется три параметра, и т. д. Конечно, если функция F имеет при данном значении параметра такую же особенность, как, например, 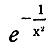, т. е. если все ее производные в данной точке 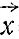₀ равны нулю, то никаким конечным числом параметров нельзя охватить все возможные качественные изменения (в смысле числа стационарных точек), которые могут произойти при сколь угодно малом возмущении этой функции (с учетом малости и ее производных). Однако строго обосновывается утверждение, что таких функций и особенностей пренебрежимо мало.

Усложнение приведенного простейшего примера может состоять, очевидно, во-первых, в увеличении числа внутренних переменных х, во-вторых, в увеличении степени F, если для начала рассматривать лишь функции F, выражаемые многочленами. Число необходимых внешних параметров u, как сказано, определяется типом рассматриваемых особенностей. Что касается числа переменных х, то, к счастью, оно оказывается не очень существенным. Если мы согласимся рассматривать только те особенности, для которых требуется небольшое число параметров для описания вида всех возможных перестроек, то окажется, что имеется только конечное число многочленов, к которым заменой переменной можно привести существенную часть функции. Точнее говоря, заменой можно привести функцию к многочлену от некоторых из переменных, начинающемуся со степеней, больших двух, и к невырожденной квадратичной форме от остальных переменных (такие квадратичные формы сами посеве не могут привести к исчезанию и рождению стационарных точек и, следовательно, к скачкам в поведении). Следующий список имеет фундаментальное значение: в нем приведены все многочлены, встречающиеся, если число параметров не больше четырех (напоминаем, что "встречающееся" означает "встречающееся и неустранимое малым возмущением"):

Среди всех этих особенностей наибольший интерес представляет сборка Уитни. Открывший ее американский тополог Хасслер Уитни первый начал систематическое исследование возможностей классификации особенностей не только (и не столько) функций, а произвольных отображений евклидовых пространств. При изучении отображений плоскости в плоскость он и открыл сборку. Основные разработанные до сих пор модели применения теории катастроф относятся как раз к сборке Уитни, в том числе и все модели, описываемые ниже.

Отметим, что, увеличивая число параметров, мы будем встречаться со все большим числом неустранимых особенностей. Полная классификация проведена до 16 параметров, что, конечно, далеко превосходит необходимое для практических применений в настоящее время.

Опишем теперь подробнее сборку Уитни. Для полного ее описания требуется 4 оси: одна для х, две для и и еще одна для значений функции. Заметим теперь, что вид самой функции для нас не важен, нам важно расположение ее критических точек. Это позволяет устранить четвертую ось и делает возможным достаточно полное описание картины на чертеже. Итак, введем три оси и для каждого значения двух параметров и отметим на первой (вертикальной) оси положение стационарных точек. Если это проделать для всех значений параметров, то стационарные точки опишут поверхность, расположенную над плоскостью параметра. Эта поверхность и будет иметь для нас основное значение. Для ее изображения мы можем воспользоваться рисунком 13, а, так как ее уравнение f' = 0, т. е. 4x³+2u₂x+u₂ = 0, что совпадает (с точностью до выбора масштаба и переименования осей) с уравнением f = x³+ux. Обратим внимание на те точки поверхности, в которых она имеет вертикальную касательную. В этих точках происходит слияние двух стационарных точек. Следовательно, их проекция даст в плоскости параметров бифуркационную диаграмму. В нашем случае мы получаем кривую с точкой возврата в нуле. Уравнение этой кривой ("полукубической параболы") 64u₁³ = 9u₂², если считать, что функция задана в точности многочленом из таблицы. Если же нам дана функция, имеющая особенность, вблизи которой ее можно привести заменой переменных к виду, указанному в таблице, то можно только сказать, что ее бифуркационная диаграмма будет кривой с точкой возврата, вблизи которой с точностью до бесконечно малых высшего порядка она имеет указанного вида уравнение (точнее, уравнение u₁³ = ku₂², где коэффициент k указывает степень раскрытия "клюва"). Над областью внутри "клюва" лежат три листа, которые парами исчезают при переходе во внешнюю область, над которой лежит один лист. Отметьте, что с разных сторон сходятся разные пары.

Теперь обратимся к самой бифуркационной диаграмме (рис. 15). Отметим две точки А и В и рассмотрим два пути от А к В. Если медленно перемещаться по верхнему пути, то не произойдет ничего особенного. Но если идти по нижнему, то в точке Д на дальней от А стороне "клюва" произойдет перескок с одного листа на другой (так как первый просто исчезает). Чтобы яснее представить себе, как это происходит, проследим за изменением графиков функции F вдоль этого пути (рис. 16). Точкой на каждом графике отмечено положение, вблизи которого в данный момент находится точка, представляющая состояние системы. Обратим внимание также на следующее явление: если вернуться от В к А по нижнему пути, то перескок произойдет в точке С на ближней к А стороне.

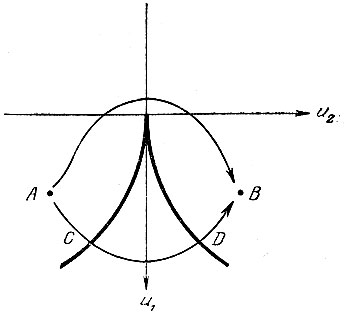
Рис. 15

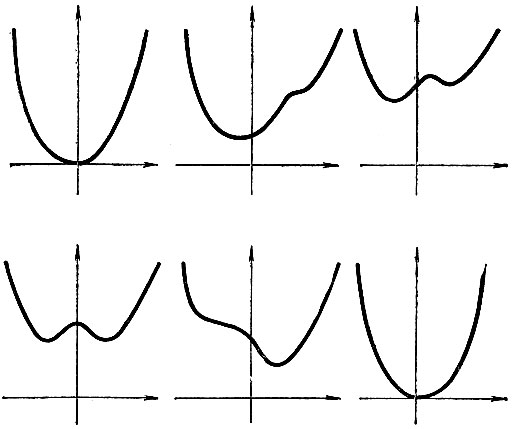
Рис. 16

Допустим теперь, что управляющие параметры сами подчиняются динамике, связывающей их обратной связью с х, как всегда медленной по сравнению с динамикой х. Естественно рассматривать эту динамику на нашей поверхности стационарных точек, так как роль быстрой динамики по х как раз и состоит в том, чтобы прижать представляющую точку к этой поверхности, вблизи же этой поверхности градиент функции нулевой, и поэтому роль этой динамики ничтожна. Рассмотрим два интересных случая, которые мы изобразим в проекции на плоскость Ouv.

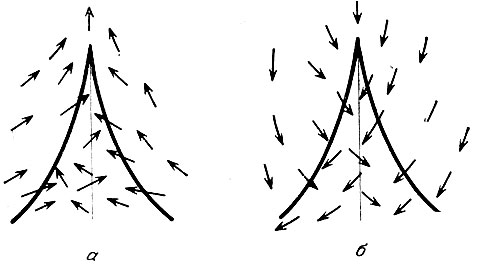
Рис. 17

1 (рис. 17, а). В этом случае точка, лежащая внутри "клюва", не может выбраться из него. Ее путь будет состоять из последовательных приближений к сторонам "клюва" и отражениям от них (в эти моменты на поверхности происходит перескок с одного листа минимумов на Iдругой). В конце концов точка пройдет вершину "клюва", и если в этой точке, как на нашем чертеже, есть составляющая, направленная во внешнюю часть плоскости, то она выйдет из "клюва" в эту "спокойную" часть плоскости.

2 (рис. 17, б). В этом случае точка также не выйдет из "клюва", но она будет удаляться от его вершины. Переходим к изложению трех работ Э. Зимана. В первом исследовании, проведенном им совместно с группой социальных психологов, был проанализирован годовой отчет одной из тюрем [4]. В качестве внутренней переменной х была выбрана степень (по определенной шкале) серьезности происшедших за данную неделю инцидентов. После длительного анализа, в проведении которого участвовал специалист-статистик, были выделены два значимых фактора: напряженность, измеряемая количеством заболевших, количеством отданных распоряжений и количеством посещений начальства, и отчужденность, измеряемая количеством наказаний и изоляций. В итоге получилась следующая картина. На 13-й неделе произошла голодная забастовка, после которой были приняты жесткие меры, в результате чего динамика только ухудшалась до бунта на 47-й неделе. После этого были проведены реформы. Интересно, что динамика близка к приведенному выше второму примеру. Последовательные максимумы возрастают. Считая, что они расположены на верхнем листе сборки, можно оценить положение вершины, коэффициент и направление оси "клюва". Он показан пунктиром. Перескоки с листа на лист совершаются раньше, чем точка достигает критической линии, что объясняется "стохастическим шумом". Интересно отметить "затишье перед бурей" на 47-й неделе.

Вторая работа Зимана [5] представляет собой анализ материалов психологического эксперимента, выяснявшего влияние алкоголя на водителей в зависимости от степени их интровертированности. Каждый водитель должен был два раза управлять тренажером-симулятором, на котором демонстрировался километровый участок дороги, первый раз в нормальном состоянии, а второй - под действием алкоголя. Отмечались ошибки и разница в затраченном времени. Был получен график, в котором по оси абсцисс отложена степень интровертированности (по некоторой шкале), а по оси ординат разница во времени. Зимана заинтересовало расхождение точек, тем более сильное, чем больше степень интровертированности. Психологи дали этому объяснение, состоящее в том, что водители либо снижали скорость, "пытаясь ехать аккуратнее", либо повышали ее, "желая продемонстрировать свое умение ездить быстро". Зиман замечает, что указанному явлению можно дать другое объяснение, предположив, что водители старались ехать со скоростью, которая субъективно кажется им нормальной.

Допустим, что решающий подсознательный механизм работает двухступенчато. Вначале происходит интегрирование информации о скорости (от шума, тряски, мельканий и многого другого), которое приводит к некоторому вероятностному распределению. Вторая ступень состоит в определении моды этого распределения, которая и будет ощущаться субъективно, как истинная скорость.

В нормальном состоянии распределение оказывается одномодальным, и мода близка (для опытного водителя) к истинной скорости автомобиля. Допустим, что алкоголь снижает "интегративную емкость системы". Считая, что элементарные "входы" дают оценки типа больше-меньше, мы получим бимодальное распределение, так как естественно предположить, что больше страдают средние, а не крайние оценки. Интроверсия может быть связана как раз с большей хрупкостью нервной системы и, в связи с этим с большим влиянием на ее интегративную емкость.

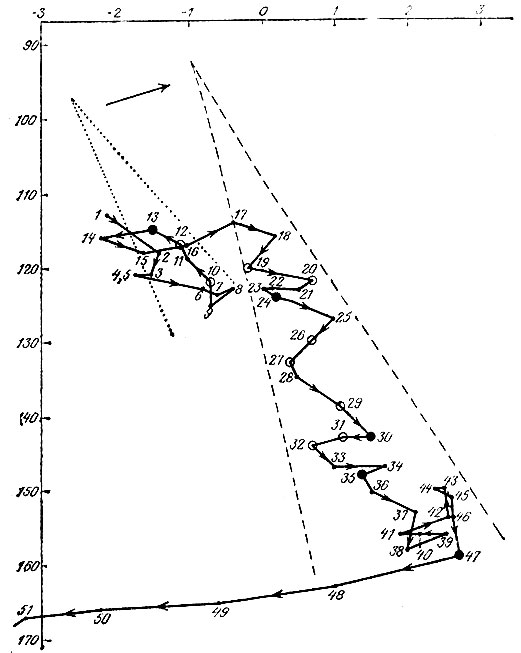
Рис. 18

В итоге мы приходим к типичной для сборки Уитни картине. В качестве внутренней переменной возьмем субъективную оценку скорости. Истинная скорость автомобиля пусть будет первым внешним параметром, который назовем нормальным, так как его увеличение ведет, вообще говоря, к увеличению внутренней переменной (если нет перескоков). За второй параметр возьмем степень интровертированности, назовем его расщепляющим, так как при его увеличении одномодальное распределение заменяется бимодальным. Нас, кстати, сейчас интересуют максимумы, а не минимумы, так что мы должны перевернуть сборку вверх ногами. Рассмотрим сечение сборки при фиксированном значении, достаточно большом, чтобы распределение стало заметно бимодальным. Будем считать, что при малых скоростях, как и при очень больших, субъективная оценка достаточно точна, но при средней скорости, близкой к обычной, водитель вообще не сможет добиться субъективного ощущения, отвечающего ей. Он будет получать то внезапное ощущение слишком большой скорости, то, пытаясь исправиться, внезапно получит ощущение слишком медленной езды. Более привычный к алкоголю водитель будет ехать на грани этого неприятного ощущения перескока, т. е. вблизи одной из сторон полукубической параболы, что и объясняет тот факт, что в 5%-ной окрестности, подобранной по методу наименьших квадратов полукубической параболы, лежит половина всех точек.

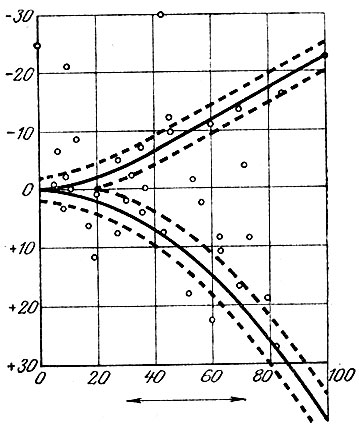
Рис. 19

Следует заметить, что этот эксперимент был проведен независимо от анализа его с точки зрения теории катастроф. В частности, нельзя ожидать, что параметр k имеет одно и то же значение для всех людей (хотя можно ожидать, что он как-то характеризует отдельного человека). Это замечание показывает, что, хотя теория катастроф имеет своей целью главным образом качественное описание, она может дать и количественные оценки. Следует отметить, что сборка Уитни, по-видимому, достаточно часто присутствует в психологических явлениях. Нам кажется, что некоторое объяснение этому содержится в работе Г. А. Голицына [7], впрочем математически неточной.

Обратимся теперь к анализу явлений в экономике, проведенному Э. Зиманом [6], а именно нестабильного поведения фондовой биржи. Состояние рынка измеряется на фондовой бирже некоторым индексом I. Однако в качестве внутренней переменной оказывается удобнее выбрать скорость его изменения J. Тогда J = 0 означает устойчивый рынок, J > 0 - оживление, J < 0 - спад. J зависит от того, какой политики вкладов придерживаются участники, и, наоборот, известное значение / влияет на них обратной связью. Э. Зиман принимает следующую' основную гипотезу: имеются два основных типа вкладчиков, одни - "фундаменталисты", которые исходят из долгосрочных прогнозов, и другие - "чартисты", которые исходят из текущего состояния рынка. К последним, как правило, относятся спекулянты. Он вводит следующие два параметра С - равный относительному количеству спекулятивных вкладов на рынке, и F - равный минимальному требованию фундаменталистов к фондам, (аналогичный параметр для чартистов скорее относится к внутренней механике рынка, чем к внешним параметрам).

Принимая естественно звучащие гипотезы, что J меняется быстрее, чем С и F, и что, когда С мало, J непрерывно возрастает вместе с F, а при большом С рынок становится нестабильным Зиман выводит, что J имеет в рассматриваемой области устойчивую особенность, которая (поскольку приняты во внимание два существенных параметра) может быть только особенностью типа сборки Уитни. Принимая дальше гипотезы: скорость С имеет тот же знак, что и J (т. е. чартисты следуют за трендом), F > 0 после большого подъема, а также после короткого падения J и F> 0,еcли J в течение некоторого времени падал и затем начал выравниваться, Зиман получает динамику, исходя из которой он дает следующее описание качественной картины поведения биржи. Рынок может быть выведен из состояния равновесия вкладами, перемещенными из других отраслей, именно благодаря длительному состоянию равновесия. При этом увеличиваются вклады фундаменталистов. Повышающийся индекс привлекает чартистов, но когда их вкладов становится слишком много, фундаменталисты начинают уменьшать свои. В результате точка пересекает критическую кривую, происходит резкий спад, чартисты уходят, и система медленно возвращается в положение равновесия. Если допустить, что эта картина отвечает реальности, она может подсказать ряд практических мер по управлению создающимися ситуациями.

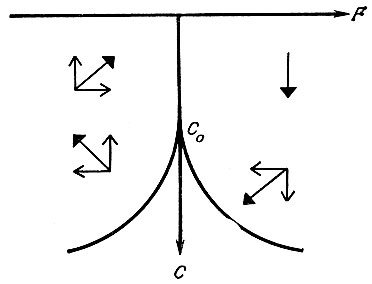
Рис. 20

Литература

1. N. Whitney. Mapping of planes into the planes, Ann. of Math, 62, 1955, p. 374-470.
2. R. Thоm. Stabilite structurelle et morphogenese. 1972. Benjamin.
3. В. И. Арнольд. Особенности гладких отображений.- "Успехи математических наук", № 23, 1968, с. 3-44.
4. Е. С. Zeeman and oths, A model for institutional disturbances, British J. of Math and Statist. Psychology, v. 29, 1976, p. 66-80.
5. E. C. Zeeman. Conflicting judgements caused by stress, British J. of Math, and Statist Psychology, v. 29, 1976, p. 19-31.
6. E. C. Zeeman. On the unstable behaviour of stock exchanges, J. of Math. Economics, v. 1, 1974, p. 39-49.
7. Г. А. Голицын. Выбор и доминанта.- В сб.: "Проблемы принятия решений". М., "Наука", 1976, с. 309-317.