Формулы прекрасных пропорций (В. М. Петров, кандидат физико-математических наук. Н. Е. Прянишников, архитектор) [1979 Беркович С.Я.

Не успели еще угаснуть споры о том, "может ли машина мыслить" и каковы ее возможности в выполнении интеллектуальных операций, как на страницах специальных и массовых изданий участились дискуссии о границах точного знания, в том числе о границах применения математических методов. Сторонники одной из позиций утверждают, что уже пора подставить под свет лучей точного знания все, что еще осталось непознанного в человеческой природе, вплоть до произведений искусства, выяснить их природу, приступить к моделированию на ЭВМ. Сторонники противоположной позиции пророчат, что именно тут-то как раз и проявится полностью качественная ограниченность точных наук, что как раз на этом "орешке" они "сломают зубы". На это им отвечают, что есть по крайней мере одна смущающая историческая аналогия: ведь еще в XIX веке полагали, что весьма серьезные преграды разделяют органический и неорганический миры; однако после того, как в 1828 году Вёлер синтезировал мочевину, граница искусственное- естественное сместилась, уступив место оппозиции "живое - неживое", а кибернетика изменила наши представления о логических возможностях "мертвой" материи.

Сейчас точные методы широко применяются в науках о человеке (социологии, истории, психологии), а "линия фронта" уже затрагивает творческие процессы и природу прекрасного.

Но споры не утихают. И в то же самое время, пока они идут, исследователи открывают новые закономерности, добывают новые знания, которым, возможно, будет суждено так или иначе примирить "враждующие" стороны. Расскажем об одной небольшой задаче из сферы прекрасного - задаче скромной, но вот уже более 2000 лет будоражащей мысли сотен художников и философов, архитекторов и искусствоведов, инженеров и психологов.

Магия "золотого сечения"

Речь пойдет о явлении, которое, по мнению некоторых специалистов, выступает и в природе, и во многих искусствах: музыке, живописи, поэзии, архитектуре. Оно относится к области пропорций, т. е. к связи частей целого друг с другом. Это так называемое "золотое сечение". Мы ограничимся только "зрительными искусствами", остановимся подробнее на геометрической интерпретации золотого сечения.

Прежде всего напомним читателям, что под многочисленными наименованиями золотого сечения (числа), "гармонического деления", "божественной пропорции" подразумевается всем известное из школьного курса математики деление отрезка в среднем и крайнем отношениях: меньший отрезок а относится к большему b так же, как больший - к их сумме:

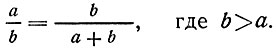
Решив это уравнение, получим численное значение этой "божественной пропорции":

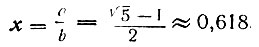
Вот это-то значение (x ≈ 0,618) и занимало умы огромного числа теоретиков и практиков искусства в течение многих веков. Часто под золотым сечением понимается обратная величина:

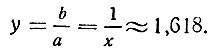
Отношению золотого сечения уделялось столь большое внимание потому, что объекты, пропорции которых ему отвечают, представлялись большинству людей самыми гармоничными, прекрасными, естественными и т. д. Если нарисовать на листе бумаги отрезок прямой (рис. 5, а) и попросить испытуемого разделить его на две части так, чтобы между ними было наиболее "гармоничное" ("красивое") соотношение, то значительная часть испытуемых поделит этот отрезок в отношении золотого сечения, т. е. в отношении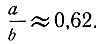

. Можно провести и другой эксперимент. Вырезать из картона несколько прямоугольников одинаковой площади, но с различным отношением сторон, и просить испытуемых выбрать тот из них, который кажется наиболее "приятным для глаза": значительная часть испытуемых при этом остановит свой выбор именно на прямоугольнике с форматом золотого сечения (рис. 5, б); такой эксперимент провел в конце прошлого века немецкий психолог Г. Т Фехнер, считающийся одним из основателей психофизики и экспериментальной эстетики. Специальная литература изобилует описаниями измерений самых различных прямоугольных объектов, которые в своей массе в среднем имеют формат золотого сечения. Измерялись форматы книг, бумажников, плиток шоколада, кирпичей, окон, дверей, контуров храмов и т. д.

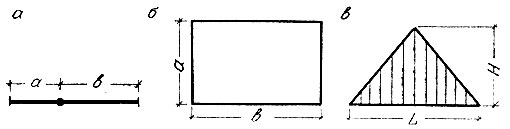
Рис. 5. Различные варианты реализации 'золотого сечения': а - деление отрезка в крайнем и среднем отношениях; б - 'божественный' прямоугольник; в - контур пирамиды Микерина

Древние египтяне, по-видимому, еще не знали золотого сечения, но в своих построениях при разбивке сооружений диагоналями полуквадрата подошли к этому отношению вплотную¹. В качестве примера такого приближения может служить меньшая из трех Великих пирамид в Гизе - пирамида Микерина: ее высота относится к основанию (рис. 5, в) как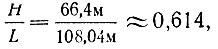

что весьма близко к значению золотого сечения.

¹ (Н. Н. Владимиров. Пропорции в египетской архитектуре.- В кн.: Всеобщая история архитектуры. Т. 1. Изд. Всесоюзной академии архитектуры. М., 1944.)

Греки усиленно занимались поисками пропорций прекрасного¹. Считается, что уже Пифагор знал арифметическую и геометрическую прогрессию, а также закон золотого сечения. То, что последнему придавалось большое значение, доказывает выбор в качестве эмблемы пифагорейской школы звездчатого пятиугольника, построение которого связано с делением радиуса круга в крайнем и среднем отношении. Однако только Платон провозгласил эстетическую закономерность этого отношения и под влиянием пифагорейцев включил его в свою эстетическую концепцию², и писал о том, что "две части или две величины не могут быть удовлетворительно связаны между собой без посредства третьей, наиболее же красивым связывающим звеном является то, которое совместно с двумя первичными величинами дает наиболее совершенное единое целое". Согласно Платону, это достигается при такой пропорции, "в которой из трех чисел, плоскостей или тел среднее так относится ко второму, а также второе к среднему, как среднее к первому. Из этого следует, что среднее может заменить первое и второе, первое и второе - среднее, и все вместе таким образом составляют неразрывное единое целое". Здесь впервые недвусмысленно указывается на необходимость связи и взаимовыводимости отдельных весьма формальных характеристик эстетических объектов, на их взаимную обусловленность единством, достигаемым в золотом сечении/

¹ (Золотое сечение, как основной морфологический закон природы и искусства (открытие профессора Цейзинга). М, 1876.)

² (Г. Д. Гримм. Пропорциональность в архитектуре. М, ОНТИ, 1935.)

То, что и греки, и римляне не только знали, но и использовали пропорцию золотого сечения, доказывает найденный при раскопках Помпеи в мастерской скульптора мерный циркуль, который ныне хранится в Неаполитанском музее¹. Его длина 146 мм; шарнир делит циркуль на два плеча - 56 и 90 мм; он почти точно установлен на золотое сечение: ⁵⁶/₉₀ = 0,622. О том же свидетельствует и анализ многих сохранившихся древних сооружений. Так, согласно Хэмбиджу², планы ряда греческих храмов образуются из нескольких прямоугольников золотого сечения.

¹ (И. Ш. Шевелев. Логика архитектурной гармонии. M/, Стройиздат, 1972.)

² (Д. Хэмбидж. Динамическая симметрия в архитектуре. М., 1936.)

В средние века пропорциям придавался мистический смысл. Секреты нахождения пропорций тщательно охранялись средневековыми зодчими. Так, профессор Гримм приводит случай, когда епископ города Утрехта поплатился жизнью за то, что хитростью сумел выведать прием нахождения пропорций сооружения храмов. Многие произведения средневекового искусства, и в первую очередь архитектуры, построены с использованием закона золотого сечения. Это в равной степени относится и к западноевропейскому, и к русскому искусству. Так, один из шедевров древнерусской архитектуры середины XII. в. - Успенская церковь Елецкого монастыря в Чернигове - имеет, по И. Ш. Шевелеву, следующие соотношения:

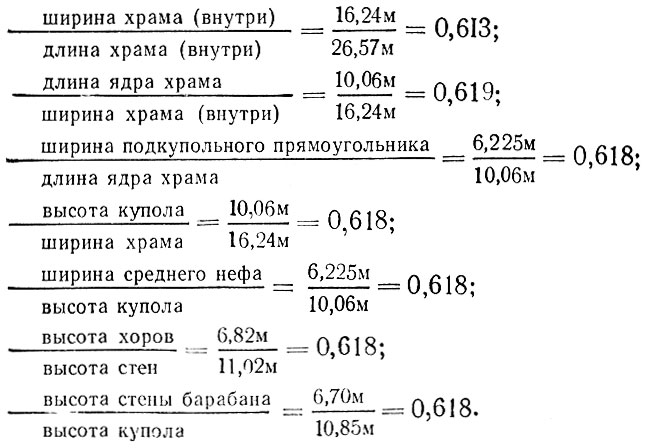
Аналогичные примеры можно привести для целого ряда произведений искусства средних веков и эпохи Возрождения¹, среди "апологетов тайных качеств божественной пропорции" были Леонардо да Винчи (который именно и назвал ее "Sectio aurea" - золотое сечение) и Кеплер (именовавший ее "Sectio divina" - божественное сечение).

¹ (См., например: Э. Мессе ль. Пропорции в античности и в средние века. М, 1936; М. Гика. Эстетика пропорций в природе и искусстве. М., 1936.)

Только в XVII-XVIII вв. интерес к золотому сечению снизился, но зато в XIX в. наступило его "новое открытие". Эта новая волна интереса к золотому сечению, своеобразный "геометрический бум" XIX столетия были отчасти обусловлены многочисленными археологическими открытиями, значительным увеличением массива обмерных чертежей. Между тем большинство вновь открываемых античных памятников, да и ряд известных, были сильно руинированы, в то время как в западноевропейской культуре XIX в. бытовала ценность целостности (в отличие, скажем, от XVIII в. с его "культом руин"); заметим также, что для XIX в. чрезвычайно характерно восполнение утраченных фрагментов античных статуй. Возникший разрыв между идеалами и реальным состоянием идеализируемых объектов пытались компенсировать за счет обширных реконструкций и реставраций; возникла сугубо практическая задача восстановления целого по сохранившейся части, вывода вертикальных членений из пропорций плана, определения общих габаритов по детали, нахождения конкретных пропорций по типовым отношениям, характерным для данного класса объектов. Иначе говоря, в анализе пропорций можно усмотреть первые попытки дешифровки языка изобразительного искусства. Эти попытки совпали по времени с интенсивным развитием экспериментальной психологии, которая (в лице Г. Т. Фехнера) отдала дань и проблеме золотого сечения.

В XX в. интерес к этой проблеме стимулировался не только развитием наук о человеке, но и непосредственно потребностями практики, удовлетворять которые должна была новая наука - инженерная психология. Появилась необходимость разработки оптимальных форм; одна из важных задач в этой области - поиск оптимального формата киноэкрана - стимулировала исследования визуального восприятия и анализ пропорций произведений живописи; такие работы проводились как советскими исследователями (в том числе С. М. Эйзенштейном), так и учеными США, ФРГ, Канады, ЧССР. И тогда оказалось, что до сих пор нет модели, которая могла бы удовлетворительно объяснить всю совокупность накопленных в этой области фактов на современном уровне научного знания. Но "ключ" к этой задаче все-таки нашелся. Попробуем взглянуть на эту проблему с теоретико-информационной точки зрения.

Информационный "ключ" к загадке

В последние десятилетия появились работы, трактующие с позиций теории информации эстетическую предпочтительность тех или иных форм, преимущественно простейших геометрических фигур и т. п. При этом зачастую в основании таких работ лежат аксиомы, правомерность которых отнюдь не является очевидной. Например, в концепции американского математика Г. Д. Биркгофа, развиваемой в последние годы западногерманским ученым М. Бензе¹, все построения базируются на постулируемой формуле М = ^O/_С, где М - эстетическая мера, О - упорядоченность и С - сложность объекта. Так или иначе большинство подобных подходов считают совершенно очевидной прямую зависимость между количеством информации, поступающей к индивиду от объекта, и эстетической оценкой объекта.

¹ (Об этой теории см., например, статьи М. Бензе и Г. Мак-Уинни в сборнике "Семиотика и искусствометрия (современные зарубежные исследования)", под ред. Ю. М. Лотмана и В. М. Петрова. М, "Мир", 1972; а также комментарии к этим статьям.)

Между тем с общетеоретических позиций такой постулат является далеко не очевидным. Не останавливаясь, однако, на этой стороне вопроса, рассмотрим ситуацию с прямоугольными формами и проследим, какую роль здесь играет информативность формы и только ли она определяет эстетическую предпочтительность объектов. Как мы увидим, окажется, что "обычная", "традиционная" теоретико-информационная концепция представляет собой лишь один из частных случаев в более общей модели.

Мы уже говорили о результатах многочисленных измерений прямоугольных объектов, которые в своей массе оказались тяготеющими к золотому сечению. Тем не менее нашелся по крайней мере один (ипритом явно из эстетической сферы!) случай, когда определение форматов было совершенно однозначным, а их статистическое распределение никак не отвечало необходимому с точки зрения золотого сечения. Речь идет о форматах картин, и поскольку такие исследования проводились в связи с конкретной и актуальной практической целью - обоснованием выбора формата киноэкрана, в этой области был собран довольно богатый статистический материал¹.

¹ (См., например, популярный обзор этого материала: Я. Бутовский. Приключения белого прямоугольника. - "Знание - сила", 1972, № 9.)

Результаты замеров большого числа картин из различных музеев мира позволили получить много интересных статистических закономерностей, связывающих формат картин с их жанровой принадлежностью, числом изображенных персонажей, "планом" изображения (в кинематографических терминах) и т. п. Но для целей нашей работы важен один результат, общий всем упомянутым исследованиям: отличие полученного распределения форматов от предпочтений по отношению к простым, равномерно окрашенным прямоугольникам. Для иллюстрации этого отличия на рис. 6 изображена кривая распределения предпочтений по отношению к "просто прямоугольникам", имеющая максимум близ пропорции y = 1,62 (а), и кривая распределения форматов 470 картин, имеющая максимум близ пропорции у = 1,3 (б); кривые условно приведены к одинаковому масштабу, для чего значение каждой из них в точке максимума распределения было принято за 100%.

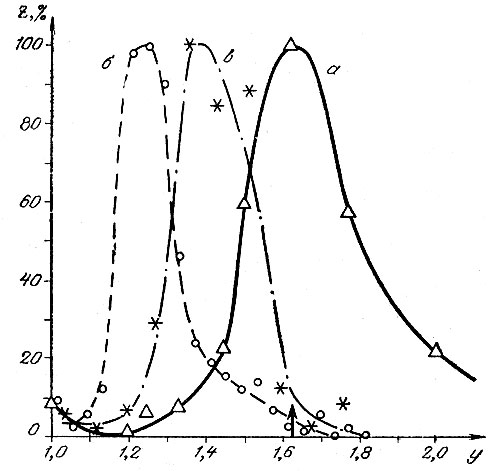
Рис. 6. Статистическое распределение: а - предпочтений прямоугольников (по результатам экспериментов Г. Т. Фехнера над 347 индивидами); б - форматов картин (наша выборка - 470 'вертикальных' картин-произведений французской живописи XVII-XIX вв. из собраний различных музеев мира); в - форматов плакатов (190 'вертикальных' плакатов, приведенных в каталоге выставки 'Три столетия французского плаката'. М., 1977)

Кривая б явео сдвинута, по сравнению с кривой а, в сторону меньших значений пропорции у, и аналогичные результаты были получены всеми авторами, которые проводили подобные обследования, и это несмотря на существенные различия в национальной, жанровой и тому подобной принадлежности обследованных картин. Заметим, что на рис. 6 приведены результаты для прямоугольников и картин "вертикального" типа (у которых высота больше ширины), но совершенно аналогичные результаты были получены и на прямоугольниках и на картинах "горизонтального" типа (у которых высота меньше ширины): максимумы распределений для прямоугольников и картин располагаются вблизи пропорций x = 0,62 и x = 0,77 соответственно. Последние значения являются обратными величинами к приводившимся ранее значениям y = 1,62 и y = 1,3 соответственно. Иначе говоря, и для "просто прямоугольников", и для картин максимумы распределений пропорций не зависят от "типа", т. е. от положения объекта по отношению к наблюдателю (вертикальное, горизонтальное). Сам вид распределений, кстати, тоже весьма близок для обоих "типов".

Таким образом, выявляется интересная закономерность: оптимальные пропорции прямоугольных объектов, когда они определяются эстетическими требованиями, практически не зависят от положения объекта по отношению к наблюдателю, но зависят от "содержательной" стороны объектов, изменяясь от пропорции, отвечающей золотому сечению (y = 1,62), - для подавляющего большинства таких объектов, до пропорции, значительно отличающейся (y = 1,3) от золотого сечения,- для картин.

Очевидно, для объяснения такого поведения прямоугольных объектов надо выявить характер воздействия их отдельных разновидностей на наблюдателя. По-видимому, факторы, связанные с индивидуальными ассоциациями (которые та или иная форма вызывает у наблюдателя), следует отбросить, так как весьма маловероятно их однонаправленное действие в таких массовых, статистических феноменах. Поэтому необходимо перейти к абстрагированной от индивидуальных особенностей наблюдателя (и индивидуальных свойств объекта) модели восприятия прямоугольной формы.

Представим себе объект, прямоугольный контур которого (произвольной пропорции) доступен наблюдателю. Как известно, процесс рассматривания объекта состоит из синтеза сигналов, поступающих в зрительный анализатор в дискретные моменты времени, отвечающие неподвижному положению зрачка, когда тот останавливается на отдельных участках объекта; последние именуются "точками фиксации". Движение зрачка между этими точками фиксации при рассматривании объекта весьма хаотично и зависит от многих обстоятельств (в частности, плотность точек фиксации на различных фрагментах объекта, как показано экспериментально, зависит от "содержания" этих фрагментов). Однако коль скоро мы строим модель, отвлекающуюся от индивидуальных особенностей наблюдателя и объекта, мы должны считать равновероятным попадание точки фиксации в любой участок объекта. Таким образом, в этой модели зрачок сканирует по поверхности объекта,беспорядочно перемещаясь от точки к точке (рис. 7). Однако полного равноправия точек, несмотря на отвлечение от "содержания" объекта, все же не существует. Дело з том, что для распознавав ния формы используется тот же компаративный механизм, который действует и в других сферах психики. В данном случае действие этого механизма сводится к тому, что для распознавания формы прямоугольника его меньшая сторона сравнивается с большей, иначе говоря, прямоугольник сравнивается с квадратом, в который он превратился бы, если бы большая сторона сжалась до размеров меньшей. А так как глаз обследует не отрезки, а фигуру, то именно такое сравнение (прямоугольника с квадратом) и должно иметь место для опознания формы. Поэтому наблюдатель должен непроизвольно спроектировать меньшую сторону прямоугольника на большую (см. рис. 7), выделить оставшийся "лишним", по сравнению с квадратом, фрагмент прямоугольника (этот фрагмент заштрихован на рис. 7) и придавать "особое значение" сигналам именно с этого фрагмента прямоугольника, потому что именно эти сигналы являются источником "разбаланса" и служат для опознания формы объекта. Для этого достаточно сравнить число сигналов, поступивших (за достаточно большой промежуток времени) от точек фиксации на этом фрагменте, с временем экспозиции. Попытаемся выяснить, как при таком механизме опознания формы могут возникнуть какие-то предпочтения тех или иных пропорций.

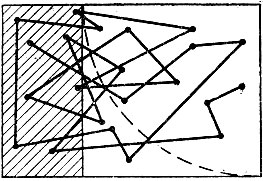
Рис. 7. Схема определения формата прямоугольника

В теории информации известно, что если сигнал может в каждый момент времени принимать какое-то одно (n-тое) значение из общего набора (n) значений и если вероятность появления этого значения обозначить через p_i (при этом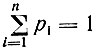

), то несомая сигналом информации составляет

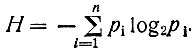/ В нашей модели сигнал вследствие упомянутого "неравноправия" точек фиксации может принимать два значения: точка фиксации расположена либо на "разбалансной" части объекта (заштрихованной на рис. 7), либо на его "квадратной" (незаштрихованной) части. Поскольку эти события являются взаимоисключающими, вероятность первого из них (p₁) в сумме с вероятностью второго (р₂) составляет единицу: p₁ + p₂ =1. Так как при анализе сигналов "особо" выделяются лишь те из них, которые поступают с "разбалансной" части объекта, следует считать H = -p₁log₂p₁. Легко показать, что во всем диапазоне значений, которые может принять вероятность P₁(0 ≤ p₁ ≤ 1), эта функция имеет лишь один экстремум - максимум при "оптимальной" вероятности p_1опт = ¹/_е ≈ 0,37.

Это означает (так как в нашей модели точки фиксации равновероятно попадают в любой участок наблюдаемой поверхности), что площадь "лишнего", разбалансного фрагмента прямоугольника, соответствующего максимуму информативности формы, должна составлять ≈ 37% от всей площади этого прямоугольника. Очень легко найти форму этого прямоугольника: а(b-а) = p_1оптab, откуда х_опт = 1 - р_1опт ≈ 0,63. Но этот "оптимальный" прямоугольник практически совпадает с прямоугольником золотого сечения (у которого x = 0,62). Отсюда можно сделать вывод: максимальная эстетическая предпочтительность прямоугольных объектов, имеющих форму золотого сечения, объясняется максимальностью информативности, или "выразительности" такой формы по сравнению со всеми другими прямоугольниками (на рис. 8 приведена кривая зависимости информативности формы от формата, из которой видно, что значения информативности при форматах х = 0,62 и х = 0,63 почти равны друг другу). Такое объяснение нам представляется гораздо более правдоподобным, чем традиционное, цитированное выше объяснение за счет "гармоничности" средней пропорциональности, что не соответствует никакому реальному механизму функционирования психики.

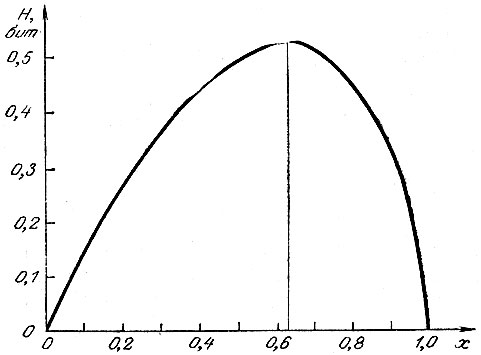
Рис. 8. Зависимость информативности Н формата прямоугольника от величины отношения его сторон х

"Парадокс картин" и его причины

Очевидно, что если целые классы объектов (притом явно подчиняющихся эстетическим критериям при их изготовлении, например, картины) статистически достоверно имеют сдвиг, всегда в одну сторону (по направлению к пропорции 1,0 и для вертикальных, и для горизонтальных типов), по отношению к золотому сечению, то на это должны быть причины, не укладывающиеся в рамки приведенной концепции. Однако поскольку мы показали, что конкретное "содержание" не может быть такой причиной, остается лишь сделать вывод о том, что ею является иная, не информативная установка зрителя при подходе к тем объектам, которые составляют это исключение.

И действительно, объекты, составляющие исключение, отличаются от неисключительных объектов той общей чертой, что площадь опознаваемого прямоугольника не равномерно окрашена, а заполнена существенно значимым изображением, которое несет информацию, по своему количеству и значимости явно превышающую информацию о форме прямоугольника. Тем не менее это, по-видимому, не значит, что форма прямоугольника может быть произвольной, и статистика распределений форматов исключений свидетельствует об этом. Попытаемся сконструировать соответствующее распределение.

Так как в случае исключений информативность формы несущественна по сравнению с информативностью "содержания", следует предположить, что оптимальной была бы форма, несущая нулевую информацию, т. е. не "отвлекающая" наблюдателя от "содержательной" стороны объекта. Но нулевую информацию, согласно вышеприведенной формуле¹ (см. также рис. 8), может нести лишь прямоугольник с p₁ = 0 или p₁ = 1, т. е. с х = 1 или х = 0. В первом случае это квадрат, второй же случай можно представить как чрезвычайно вытянутый прямоугольник, вырождающийся в пределе (при х → 0) в прямую линию "без ширины".

¹ (Уточним, что здесь всюду имеется в виду информация о пропорциях прямоугольника, а не о самом факте появления прямоугольника (последняя информация считается постоянной).)

В живописи второй случай приводит к ряду осложнений. Картина утрачивает единство, поскольку становится затруднительным помещение ее всей в поле зрения при масштабе, позволяющем воспринимать "содержание". Между тем традиции большинства культур требуют "центрирования" плоскостей картин, т. е. наличия в пространстве точки (расположенной либо у зрителя, либо за изобразительной плоскостью), в которой сходятся лучи, соединяющие изображаемые объекты с их представлениями на плоскости картины; поэтому слишком сильно вытянутая (безразлично, в высоту или в ширину) картина должна восприниматься как совокупность фрагментов и последовательно "прочитываться" как текст, по типу некоторых древнеегипетских настенных росписей. Впрочем, все эти требования удовлетворяются в некоторых ветвях традиционных культур Востока, например, в искусстве Японии, где отсутствие перспективного изображения и пантеистический характер миросозерцания ("растворенность" "божественного начала" во всех точках пространства и, отсюда, их относительное принципиальное "равноправие") снимают указанные ограничения и приводят к господству сильно вытянутых форм. Но эти ограничения присутствуют в большинстве современных культур, которые в рамках данной работы только нас и интересуют, и поэтому такие сильно вытянутые формы мы далее не рассматриваем.

Следовательно, остается рассмотреть лишь проблему квадрата и форм, близких к квадратным, т. е. чуть вытянутых либо в длину, либо в высоту. Иначе говоря, получив принципиальную предпочтительность таких форм, следует проверить их на "устойчивость", т. е. убедиться в реальной осуществимости или неосуществимости высокой частоты встречаемости таких объектов. Для этого рассмотрим ситуацию, когда, допустим, создаются преимущественно квадратные объекты, что отвечает распределению объектов по форматам, которое на рис. 10 показано сплошной линией. Но по тем или иным причинам (например, из-за необходимости передачи определенного "содержания") создаются отдельные картины, отличающиеся от квадратных в ту или иную сторону, так как квадрат в качестве стандарта не задан, а небольшие отклонения от него мало что меняют, тем более что в случае картин формат прямоугольника играет третьестепенную роль, несет весьма мало информации по сравнению с "содержанием".

Пока эти отклонения от квадрата малы (рис. 9), форма воспринимается как квадратная. Но по достижении некоторого порога различения (который во всех таких простейших случаях сравнения длин, интенсивностей и т. п. составляет около 10-15%) ситуация изменяется. Форма уже может восприниматься как ориентированная либо в вертикальном, либо в горизонтальном направлении, а эти "прецеденты" создадут в психике зрителя установку на различение между этими двумя типами (в силу действия принципа "определенности соотнесения" объекта с соответствующим "эталоном", общего для всех психических механизмов). Положение усугубляется еще и тем, что вертикаль и горизонталь являются "особыми" осями, которые служат индивиду как для ориентации в окружающем пространстве, так и (в качестве границ картины) для оценки свойств пространства, изображенного на картине. Последнее обстоятельство также делает неизбежным выделение, подчеркивание форматом этих осей, а так как ориентация на обе оси сразу невозможна, то хотя бы одной из осей. (Это, кстати, предъявляет свои требования и к ориентации композиции самого изображения в одном из двух "особых" направлений - вертикальном или горизонтальном, а посему формат также должен согласовываться с ней своей ориентацией, либо, чаще, совпадая, либо, реже, "играя" на диаметрально противоположной ориентации.)

Рис. 9. Изображения прямоугольников с отношением сторон: 1:1 (а); 1:1,05 (б); 1:1,10 (в); 1:1,15 (г); 1:1,20 (д)

Сказанное делает необходимым выделение формата в качестве знака принадлежности к одному из двух типов (вертикальному или горизонтальному). Для выполнения этого требования достаточно, чтобы создаваемые объекты отличались от квадратной формы на величину, не меньшую, чем порог различения, чтобы можно было сразу "приписать" объект к тому или иному типу. Такое отличие соответствует "сдвигу" объектов в стороны, показанные на рис. 10 стрелками. Это приводит к образованию двух, не смешиваемых друг с другом, группировок объектов. (Кстати, при таком небольшом сдвиге по отношению к квадрату информативность меняется сравнительно мало.) Автоматически сами квадратные и почти квадратные формы становятся как бы "запрещенными", статистически дающими меньшую эстетическую оценку, чем все близкие к ним формы. Это то самое "отрицательное отношение к квадрату", которое в случае картин так удивляло еще Г. Т. Фехнера своим несоответствием "всем теоретическим соображениям".

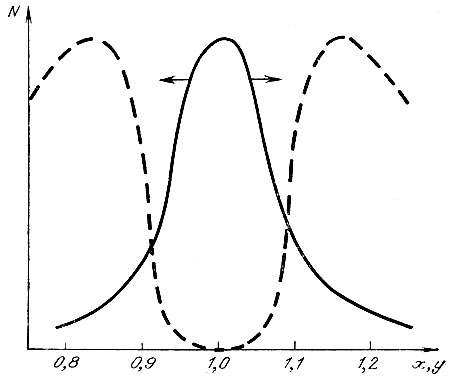
Рис. 10. 'Неустойчивость' квадратного формата и форматов, близких к квадратному

Таким образом, несмотря на принципиальную предпочтительность квадратной формы, в реальных условиях функционирования она должна быть социально неустойчивой и "распадаться" на две группы форм, которые близки друг к другу, но не пересекаются. Следствием такого процесса своеобразной "самоорганизации" форматов должно быть распределение, имеющее вид показанного пунктиром на рис. 10. Отличительными чертами этого распределения должны быть:

а) присутствие двух максимумов по обе стороны от формата х = 1;

б) наличие резкого, глубокого провала в области близ х = 1;

в) положение каждого из максимумов между форматом, отвечающим золотому сечению (т. е. х ≈ 0,62 и y = 1,62 для горизонтальных и вертикальных объектов соответственно), и форматом, обеспечивающим отличие от квадрата на величину порога различения (т. е. х_опт <0,90 и y_опт > 1,10 соответственно);

г) асимметричность каждой из половин распределения (так как "запрет" со стороны квадратной формы-действует гораздо сильнее, чем слабый спад кривой по-другую сторону от максимума).

Имеющиеся в литературе, а также наши статистические данные свидетельствуют о том, что во всех выборках эти условия (а-г) всегда выполнялись. В качестве иллюстрации на рис. 11, 12 приведены распределения картин - различных жанров и различных эпох - по форматам (выборка объемом 978 картин французской живописи в собраниях различных музеев мира). Легко видеть, что все распределения обладают максимумами, расположенными при одних и тех же значениях формата; изменяется лишь само значение (абсолютная величина) функции в точке максимума. Положение максимума оказалось практически не зависящим также и<от абсолютных размеров картин. Такая высокая устойчивость оптимального формата служит хорошим аргументом в пользу описанной модели. >

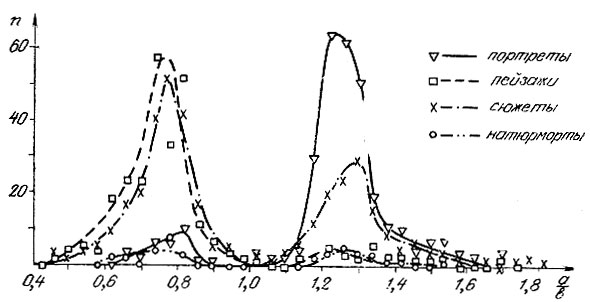
Рис. 11. Распределение картин различных жанров по форматам

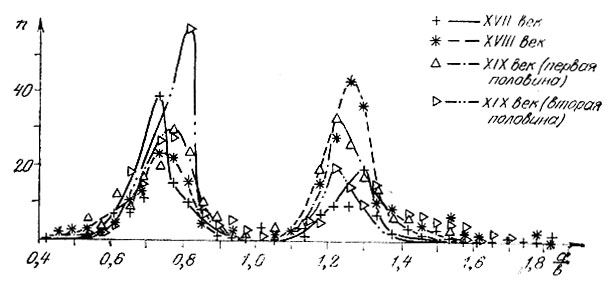
Рис. 12. Распределение картин различных веков по форматам

Вернемся теперь к рис. 6, на котором, помимо распределений для "просто прямоугольников" и картин,, представлена также кривая, относящаяся к плакатам. Последняя кривая занимает промежуточное положение между двумя первыми. В свете всего сказанного ранее это не удивительно: ведь по характеру своего восприятия плакаты действительно занимают промежуточное положение между "просто цветовым пятном" и картиной; это отражается и на положении кривой их распределения по форматам, что также служит хорошим подтверждением адекватности модели реальности.

Итак, и "правила", и "исключения" из закона золотого сечения, относящиеся к эстетической предпочтительности прямоугольников, хорошо укладываются в рамки единой простой модели. Оказывается, что достаточно знать установку зрителя, чтобы сконструировать характер статистического распределения форм соответствующих объектов.

Здесь уместно сделать небольшое отступление, посвященное теоретико-методическим аспектам подобного "конструирования". В рассмотренных нами случаях ("просто прямоугольников" и картин) было выполнено не что иное, как наложение определенного критерия на результат деятельности определенного механизма восприятия. В случае "просто прямоугольников" роль такого механизма играло сравнение площадей "разбалансного" и "квадратного" фрагментов. Роль же критерия играла установка зрителя на максимизацию информативности. (Кстати, если считать, что точки фиксации концентрируются в основном на контуре фигуры, и взять за основу сравнение не площадей, а длин сторон а и b, то критерий максимизации информативности даст уравнение b-а = p_1опти, с тем же решением х_опт ≈ 0,63; аналогичные рассуждения приложимы и к делению отрезка в среднем и крайнем отношении, представленному на рис. 5, а.).

В случае картин в нашем анализе фигурировали уже два механизма восприятия, только что упомянутый компаративный механизм определения формата и другой механизм - отделения вертикальных композиций от горизонтальных (связанный с соответствующими содержательными ассоциациями); эти два механизма действуют на двух разных уровнях переработки информации индивида. Критериев - тоже два: на нижнем из двух этих уровней (где действует компаративный механизм) работает установка на минимизацию информативности, а на верхнем (где функционируют содержательные ассоциации) - установка на максимизацию различия между двумя композиционными типами. Совместное действие критериев разных уровней и дает тот результат, который мы можем наблюдать в эмпирической реальности.

Заметим, что указанные механизмы и критерии отнюдь не являются единственными. Даже в случае "просто прямоугольников" можно отыскать такую ситуацию, когда не будет действовать механизм определения формата; видимо, этим объясняется то, что Г. Т. Фехнеру не удалось получить феномен предпочтения золотого сечения в эксперименте с предъявлением прямоугольников маленьким детям (у которых данный механизм еще недостаточно сформировался). Можно найти и такую ситуацию, в которой не будет действовать (или будет действовать ослабленно) критерий - установка на максимум информативности; известно, например, что в культурно-сопоставительном исследовании канадских и японских девушек последние показали меньшее предпочтение вытянутых форматов (и в том числе формата золотого сечения), чем первые; по-видимому, это связано с более сильным проявлением у японских девушек "канонической" установки на равенство сторон, т. е. на стремление к квадрату.

В общем случае надо учитывать все реальное разнообразие и механизмов, и соответствующих им критериев, действующих на разных уровнях переработки информации. Тогда можно предсказывать воздействие конструируемых объектов на индивида; понятно, что пока это можно делать лишь применительно к довольно простым случаям, с весьма "прозрачными" для исследователя механизмами и критериями.

Мы привели решение лишь одной из задач сферы "прекрасных пропорций". Оно показывает не только применимость точных методов к анализу этой сложной сферы, но и необходимость весьма глубокого содержательного рассмотрения подобных проблем, без которого даже самые совершенные модельные построения могут остаться пустой "игрой в формулы", лишенной связи с реальностью.

Формулы прекрасных пропорций (В. М. Петров, кандидат физико-математических наук. Н. Е. Прянишников, архитектор)

Магия "золотого сечения"

Информационный "ключ" к загадке

"Парадокс картин" и его причины

Литература