Число 10101

После сказанного о числе 1001 уже не будет неожиданностью увидеть в витринах нашей галереи число 10101. Вы догадаетесь, какому именно свойству обязано это число такою честью. Оно, как и число 1001, дает удивительный результат при умножении, но не трехзначных чисел, а двузначных; каждое двузначное число, умноженное на 10101, дает в результате само себя, написанное трижды. Например:

 73 X 10101 = 737373, 
 21 X 10101 = 212121. 

Причина уясняется из следующей строки:

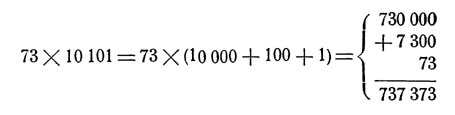
Можно ли проделывать с помощью этого числа фокусы необычайного отгадывания, как с помощью числа 1001?

Да, можно. Здесь возможно даже обставить фокус разнообразнее, если иметь в виду, что 10 101 есть произведение четырех простых чисел:

10101 = 3 X 7 X 13 X 37.

Предложив товарищу задумать какое-нибудь двузначное число, вы предлагаете второму приписать к нему то же число, а третьему - приписать то же число еще раз. Четвертого вы просите разделить получившееся шестизначное число, например, на 7; пятый товарищ должен разделить полученное частное на 3; шестой делит то, что получилось, на 37, и, наконец, седьмой делит этот результат на 13, причем все четыре деления выполняются без остатка. Результат последнего деления вы просите передать первому товарищу: это и есть задуманное им число.

При повторении фокуса вы можете внести в него некоторое разнообразие, обращаясь каждый раз к новым делителям. А именно, вместо четырех множителей 3 X 7 X 13 X 37 можете взять следующие группы трех множителей: 21 X 13 X 37; 7 X 39 X 37; 3 X 91 X 37; 7 Х 13 Х 111.

Число это - 10101, - пожалуй, даже удивительнее волшебного числа Шехеразады, хотя и менее его известно своими поразительными свойствами. О нем писалось, впрочем, еще двести лет назад в "Арифметике" Магницкого, в главе, где приводятся примеры умножения "с некоим удивлением". С тем большим основанием должны мы включить его в наше собрание арифметических диковинок.