
Логарифмы на эстраде
Самый поразительный из номеров, выполняемых перед публикой профессиональными счетчиками, без сомнения следующий. Предуведомленные афишей, что счетчик-виртуоз будет извлекать в уме корни высоких степеней из многозначных чисел, вы заготовляете дома путем терпеливых выкладок 31-ю степень какого-нибудь числа и намерены сразить счетчика 35-значным числовым линкором. В надлежащий момент вы обращаетесь к счетчику со словами:
- А попробуйте извлечь корень 31-й степени из следующего 35-значного числа! Запишите, я продиктую.
Виртуоз-вычислитель берет мел, но прежде чем вы успели открыть рот, чтобы произнести первую цифру, у него уже написан результат: 13.
Не зная числа, он извлек из него корень, да еще 31-й степени, да еще в уме, да еще с молниеносной быстротой!...
Вы изумлены, уничтожены, а между тем во всем этом нет ничего сверхъестественного. Секрет просто в том, что существует только одно число, именно 13, которое в 31-й степени дает 35-значный результат. Числа, меньшие 13, дают меньше 35-цифр, большие - больше.
Откуда, однако, счетчик знал это? Как разыскал он число 13? Ему помогли логарифмы, двузначные логарифмы, которые он помнит наизусть для первых 15-20 чисел. Затвердить их вовсе не так трудно, как кажется, особенно если пользоваться тем, что логарифм составного числа равен сумме логарифмов его простых множителей. Зная твердо логарифмы 2, 3 и 7*, вы уже знаете логарифмы чисел первого десятка; для второго десятка требуется помнить логарифмы еще четырех чисел.
* (Напомним, что lg 5 = lg 10/2 = 1 - lg 2.)
Как бы то ни было, эстрадный вычислитель мысленно располагает следующей табличкой двузначных логарифмов:
| Числа | Лог. | Числа | Лог. |
|---|---|---|---|
| 2 | 0,30 | 11 | 1,04 |
| 3 | 0,48 | 12 | 1,08 |
| 4 | 0,60 | 13 | 1,11 |
| 5 | 0,70 | 14 | 1,15 |
| 6 | 0,78 | 15 | 1,18 |
| 7 | 0,85 | 16 | 1,20 |
| 8 | 0,90 | 17 | 1,23 |
| 9 | 0,95 | 18 | 1,26 |
| * | * | 19 | 1,28 |
Изумивший вас математический трюк состоял в следующем:
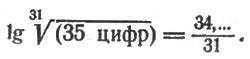
Искомый логарифм может заключаться между
34/31 и 34,99/31 или между 1,09 и 1,13.
В этом интервале имеется логарифм только одного целого числа, именно 1,11 - логарифм 13. Таким путем и найден ошеломивший вас результат. Конечно, чтобы быстро проделать все это в уме, надо обладать находчивостью и сноровкой профессионала, но по существу дело, как видите, достаточно просто. Вы и сами можете теперь проделывать подобные фокусы, если не в уме, то на бумаге.
Пусть вам предложена задача: извлечь корень 64-й степени из 20-значного числа.
Не осведомившись о том, что это за число, вы можете объявить результат извлечения: корень равен 2.
В самом деле 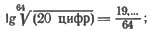 он должен следовательно, заключаться между 19/64 и 19,99/64, т. е. между 0,29 и 0,32. Такой логарифм для целого числа только один: 0,30..., т. е. логарифм числа 2.
он должен следовательно, заключаться между 19/64 и 19,99/64, т. е. между 0,29 и 0,32. Такой логарифм для целого числа только один: 0,30..., т. е. логарифм числа 2.
Вы даже можете окончательно поразить загадчика, сообщив ему, какое число он собирался вам продиктовать: знаменитое "шахматное" число
264 = 18446744073709551616.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'