Ответственный расчет

В вычислительной практике встречаются такие чисто арифметические выкладки, выполнение которых без помощи облегчающих методов алгебры чрезвычайно затруднительно. Пусть требуется, например, найти результат таких действий:

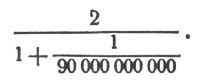
(Вычисление это необходимо для того, чтобы установить, вправе ли техника, имеющая дело со скоростями движения тел, малыми по сравнению со скоростью распространения электромагнитных волн, пользоваться прежним законом сложения скоростей, не считаясь с теми изменениями, которые внесены в механику теорией относительности. Согласно старой механике тело, участвующее в двух одинаково направленных движениях со скоростями v₁ и v₂ километров в секунду, имеет скорость (v₁ + v₂) километров в секунду. Новое же учение дает для скорости тела выражение

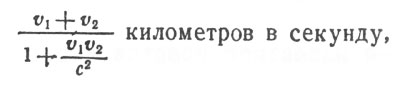
где с - скорость распространения света в пустоте, равная приблизительно 300000 километров в секунду. В частности, скорость тела, участвующего в двух одинаково направленных движениях, каждое со скоростью 1 километр в секунду, по старой механике равно 2 километрам в секунду, а по новой как раз

Насколько же разнятся эти результаты? Уловима ли разница для тончайших измерительных приборов? Для выяснения этого важного вопроса и приходится выполнить указанное выше вычисление.)

Сделаем это вычисление двояко: сначала обычным арифметическим путем, а затем покажем, как получить результат приемами алгебры. Достаточно одного взгляда на приведенные далее длинные ряды цифр, чтобы убедиться в неоспоримых преимуществах алгебраического способа.

Прежде всего преобразуем нашу "многоэтажную" дробь:

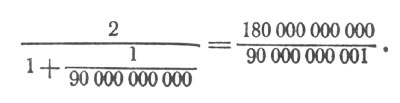
Произведем теперь деление числителя на знаменатель:

Вычисление, как видите, утомительное, кропотливое; в нем легко запутаться и ошибиться. Между тем, для решения задачи важно в точности знать, на котором именно месте обрывается ряд девяток и начинается серия других цифр.

Сравните теперь, как коротко справляется с тем же расчетом алгебра. Она пользуется следующим приближенным равенством: если а - весьма малая дробь, то

1/(1 + a) ≈	1 - a,

где знак ≈ означает "приближенно равно".

Убедиться в справедливости этого утверждения очень просто: сравним делимое 1 с произведением делителя на частное:

1 = (1 + а)(1 - а),

т. е.

1 = 1 - а2.

Так как а - весьма малая дробь (например, 0,001), то а² еще меньшая дробь (0,000001), и ею можно пренебречь.

Применим сказанное к нашему расчету^*:

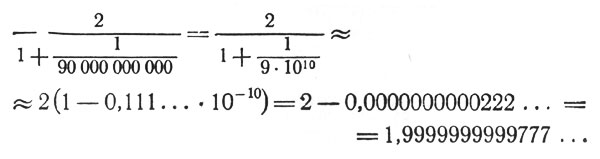
^* (Мы пользуемся далее приближенным равенством A/(1 + a) ≈ A(1 - a).)

Мы пришли к тому же результату, что и раньше, но гораздо более коротким путем.

(Читателю, вероятно, интересно знать, каково значение полученного результата в поставленной нами задаче из области механики. Этот результат показывает, что ввиду малости рассмотренных скоростей по сравнению со скоростью света уклонение от старого закона сложения скоростей практически не обнаруживается: даже при таких огромных скоростях, как 1 км/сек, оно сказывается на одиннадцатой цифре определяемого числа, а в обычной технике ограничиваются 4-6 цифрами. Мы вправе поэтому утверждать, что новая, эйнштейнова, механика практически ничего не меняет в технических расчетах, относящихся к "медленно" (по сравнению с распространением света) движущимся телам. Есть, однако, одна область современной жизни, где этот безоговорочный вывод следует принимать с осторожностью. Речь идет о космонавтике. Ведь уже сегодня мы достигли скоростей порядка 10 км/сек (при движении спутников и ракет). В этом случае расхождение классической и эйнштейновой механики скажется уже на девятом знаке. А ведь не за горами еще большие скорости...)