В миллионы раз быстрее

Электрический прибор, называемый триггером, содержит две электронные лампы^* (т. е. примерно такие лампы, которые применяются в радиоприемниках). Ток в триггере может идти только через одну лампу: либо через "левую", либо через "правую". Триггер имеет два контакта, к которым может быть

^* (Существо дела не меняется, если вместо электронных ламп используются транзисторы или так называемые твердые (пленочные) схемы.)

извне подведен кратковременный электрический сигнал (импульс), и два контакта, через которые с триггера поступает ответный импульс. В момент прихода извне электрического импульса триггер переключается: лампа, через которую шел ток, выключается, а ток начинает идти уже через другую лампу. Ответный импульс подается триггером в тот момент, когда выключается правая лампа и включается левая.

Проследим, как будет работать триггер, если к нему подвести один за другим несколько электрических импульсов. Будем характеризовать состояние триггера по его правой лампе: если ток через правую лампу не идет, то скажем, что триггер находится в "положении 0", а если ток через правую лампу идет,- то в "положении 1".

Пусть первоначально триггер находился в положении 0, т. е. ток шел через левую лампу (рис. 1). После первого импульса ток будет идти через правую лампу, т. е. триггер переключится в положение 1. При этом ответного импульса с триггера не поступит, так как ответный сигнал подается в момент выключения правой (а не левой) лампы.

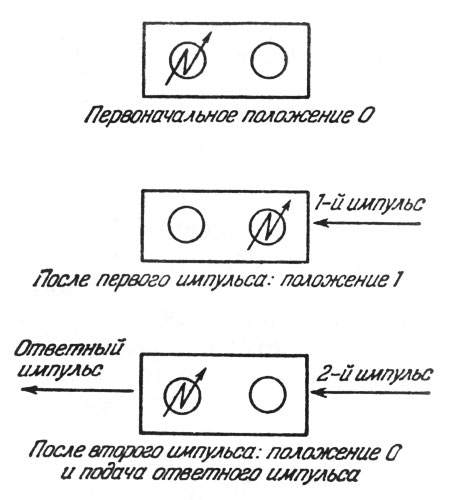
Рис. 1. Пусть первоначально триггер находился в положении 0, т. е. ток шел через левую лампу

После второго импульса ток будет идти уже через левую лампу, т. е. триггер снова попадет в положение 0. Однако при этом триггер подаст ответный сигнал (импульс).

В результате (после двух импульсов) триггер снова придет к начальному состоянию. Поэтому после третьего импульса триггер (как и после первого) попадет в положение 1, а после четвертого (как и после второго) - в положение 0 с одновременной подачей ответного сигнала и т. д. После каждых двух импульсов состояния триггера повторяются.

Представим себе теперь, что имеются несколько триггеров и что импульсы извне подводятся к первому триггеру, ответные импульсы первого триггера подводятся ко второму, ответные импульсы второго - к третьему и т. д. (на рис. 2 триггеры расположены один за другим справа налево). Проследим, как будет работать такая цепочка триггеров.

Рис. 2. Триггеры расположены один за другим справа налево

Пусть сначала все триггеры находились в положениях 0. Например, для цепочки, состоящей из пяти триггеров, мы имели комбинацию 00000. После первого импульса первый триггер (самый правый) попадет в положение 1, а так как ответного импульса при этом не будет, то все остальные триггеры останутся в положениях 0, т. е. цепочка будет характеризоваться комбинацией 00001. После второго импульса первый триггер выключится (попадает в положение 0), но подаст при этом ответный импульс, благодаря чему включится второй триггер. Остальные триггеры останутся в положениях 0, т. е. получится комбинация 00010. После третьего импульса включится первый триггер, а остальные не изменят своих положений. Мы будем иметь комбинацию 00011. После четвертого импульса выключится первый триггер, подав ответный сигнал; от этого ответного импульса выключится второй триггер и также даст ответный импульс; наконец, от этого последнего импульса включится третий триггер. В результате мы получим комбинацию 00100.

Аналогичные рассуждения можно продолжать и далее. Посмотрим, что при этом получается:

1-й импульс - комбинация 00001
2-й импульс - комбинация 00010
3-й импульс - комбинация 00011
4-й импульс - комбинация 00100
5-й импульс - комбинация 00101
6-й импульс - комбинация 00110
7-й импульс - комбинация 00111
8-й импульс - комбинация 01000
..............................

Мы видим, что цепочка триггеров "считает" поданные извне сигналы и своеобразным способом "записывает" число этих сигналов. Нетрудно видеть, что "запись" числа поданных импульсов происходит не в привычной для нас десятичной системе, а в двоичной системе счисления.

Всякое число в двоичной системе счисления записывается нулями и единицами. Единица следующего разряда не в десять раз (как в обычной десятичной записи), а только в два раза больше единицы предыдущего разряда. Единица, стоящая в двоичной записи на последнем (самом правом) месте, есть обычная единица. Единица следующего разряда (на втором месте справа) означает двойку, следующая единица означает четверку, затем восьмерку и т. д.

Например, число 19 = 16 + 2 + 1 запишется в двоичной системе в виде 10011.

Итак, цепочка триггеров "подсчитывает" число поданных сигналов и "записывает" его по двоичной системе счисления. Отметим, что переключение триггера, т. е. регистрация одного приходящего импульса, продолжается всего... стомиллионные доли секунды! Современные триггерные счетчики могут "подсчитывать" десятки миллионов импульсов в секунду. Это в миллионы раз быстрее, чем счет, который может проводить человек без всяких приборов: глаз человека может отчетливо различать сигналы, следующие друг за другом не чаще, чем через 0,1 сек.

Если составить цепочку из двадцати триггеров, т. е. записывать число поданных сигналов не более чем двадцатью цифрами двоичного разложения, то можно "считать" до 2²⁰ - 1; это число больше миллиона. Если же составить цепочку из 64 триггеров, то можно записать с их помощью знаменитое "шахматное число".

Возможность подсчитывать миллионы сигналов в секунду очень важна для экспериментальных работ, относящихся к ядерной физике. Например, можно подсчитывать число частиц того или иного вида, вылетающих при атомном распаде.