
Решения головоломок 101-130
101. Можно выполнить требуемую работу, раскрыв только три звена. Для этого надо освободить звенья одного обрывка и соединить ими концы остальных четырех обрывков.
102. Чтобы решить эту задачу, нужно прежде всего припомнить из естественной истории, сколько ног у жуков и сколько у пауков: у жука 6 ног, у паука - 8.
Зная это, предположим, что в коробке были одни только жуки, числом 8 штук. Тогда всех ног было бы 6X8 = 48, на 6 меньше, чем указано в задаче. Заменим теперь одного жука пауком. От этого число ног увеличится на 2, потому что у паука не 6 ног, а 8.
Ясно, что если мы сделаем три такие замены, мы доведем общее число ног в коробке до требуемых 54. Но тогда из 8 жуков останется только 5, остальные будут пауки.
Итак, в коробке было 5 жуков и 3 паука.
Проверим: у 5 жуков 30 ног, у 3 пауков 24 ноги, а всего 30 + 24 = 54, как и требует условие задачи.
Можно решить задачу и иначе. А именно: можно предположить, что в коробке были только пауки, 8 штук. Тогда всех ног оказалось бы 8 X 8 = 64, - на 10 больше, чем указано в условии. Заменив одного паука жуком, мы уменьшим число ног на 2. Нужно сделать 5 таких замен, чтобы свести число ног к требуемым 54. Иначе говоря, из 8 пауков надо оставить только 3, а остальных заменить жуками.
103. Если бы вместо плаща, шляпы и галош куплено было только две пары галош, то пришлось бы заплатить не 20 руб., а на столько меньше, на сколько галоши дешевле плаща с шляпой, т. е. на 16 руб. Мы узнаем, следовательно, что две пары галош стоят 20-16 = 4 руб., отсюда стоимость одной пары - 2 руб.
Теперь стало известно, что плащ и шляпа вместе стоят 20-2 = 18 руб., причем плащ дороже шляпы на 9 руб. Рассуждаем, как прежде: вместо плаща с шляпой, купим две шляпы. Мы заплатим не 18 руб., а меньше на 9 руб. Значит, две шляпы стоят 18-9 = 9 руб., откуда стоимость одной шляпы - 4 руб. 50 коп.
Итак, вот стоимость вещей: галоши - 2 руб., шляпа - 4 руб. 50 коп., плащ - 13 руб. 50 коп.
104. Продавец имел в виду корзину с 29 яйцами. Куриные яйца были в корзинах с обозначениями 23, 12 и 5 утиные - в корзинах с числами 14 и 6.
Проверим. Всего куриных яиц оставалось:
23 + 12 + 5 = 40.
Утиных
14 + 6 = 20.
Куриных вдвое больше, чем утиных, как и требует условие задачи.
105. В этой задаче нечего объяснять: самолет совершает перелет в обоих направлениях в одинаковое время, потому что 80 мин. = 1 ч. 20 м.
Задача рассчитана на невнимательного читателя, который может подумать, что между 1 ч. 20 м. и 80 мин. есть разница. Как ни странно, но людей, попадающихся на этот крючок, оказывается немало, притом среди привыкших делать расчеты их больше, чем среди малоопытных вычислителей. Причина кроется в привычке к десятичной системе мер и денежных единиц. Видя обозначение: "1 ч. 20 м." и рядом с ним "80 мин.", мы невольно оцениваем различие между ними, как разницу между 1 р. 20 к. и 80 коп. На эту психологическую ошибку и рассчитана задача.
106. Разгадка недоумения в том, что один из отцов приходился другому сыном. Всех было не четверо, а трое: дед, сын и внук. Дед дал сыну 150 руб., а тот передал из них 100 руб. внуку (т. е. своему сыну), увеличив собственные капиталы, следовательно, всего на 50 руб.
107. Первую шашку можно поместить на любое из 64 полей доски, т. е. 64 способами. После того как первая поставлена, вторую шашку можно поместить на какое-либо из прочих 63 полей. Значит к каждому из 64 положений первой шашки можно присоединить 63 положения второй шашки. Отсюда общее число различных положений двух шашек на доске
64 X 63 = 4032.
108. Наименьшее целое число, какое можно написать двумя цифрами, не 10, как думают, вероятно, иные читатели, а единица, выраженная таким образом:
1/1, 2/2, 3/3, 4/4 и т. д. до 9/9.
Знакомые с алгеброй прибавят к этим выражениям еще и ряд других обозначений:
1°, 2°, 3°, 4° и т. д. до 9°,
потому, что всякое число в нулевой степени равно единице*.
* (Но неправильны были бы решения 0/0 или 0°; эти выражения вообще не имеют смысла.)
109. Надо представить единицу как сумму двух дробей
148/296 +35/70 = 1.
Знающие алгебру могут дать еще и другие ответы:
1234567890; 2345679-8-1
и т. п., так как число в нулевой степени равно единице.
110. Два способа таковы:
9 99/99 = 10, 99/9 - 9/9 = 10.
Кто знает алгебру, тот может прибавить еще несколько решений, например:
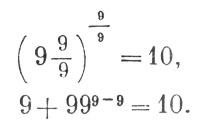
111. Вот 4 решения:
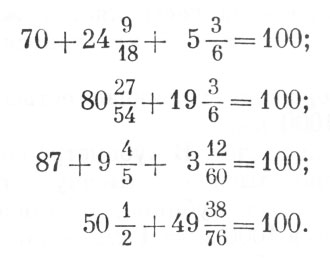
112. Число 100 можно выразить пятью одинаковыми цифрами, употребив в дело единицы, тройки и - всего проще - пятерки
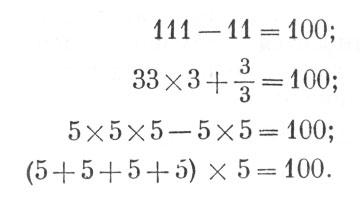
113. На вопрос задачи часто отвечают: 1111. Однако можно написать число во много раз больше - именно 11 в одиннадцатой степени: 1111. Если у вас есть терпение довести вычисление до конца (с помощью логарифмов можно выполнять такие расчеты гораздо скорее), вы убедитесь, что число это больше 280 миллиардов. Следовательно, оно превышает число 1111 в 250 миллионов раз.
114. Заданный пример деления может соответствовать четырем различным случаям, а именно:
1337174 : 943 = 1418; 1343784 : 949 = 1416; 1200474 : 846 = 1419; 1202464 : 848 = 1418.
115. Этот пример отвечает только одному случаю деления:
7375428413 : 125473 = 58781.
Обе последние, весьма нелегкие задачи были впервые опубликованы в американских изданиях: "Математическая газета", 1920 г. и "Школьный мир", 1906 г.
116. В квадратном метре тысяча тысяч квадратных миллиметров. Каждая тысяча приложенных друг к другу миллиметровых квадратиков составляет 1 м; тысяча тысяч их составляет 1000 м, т. е. 1 км: полоска вытянется на целый километр.
117. Ответ поражает неожиданностью: столб возвышался бы на... 1000 км.
Сделаем устный расчет. В кубометре содержится кубических миллиметров тысяча X тысячу X тысячу. Каждая тысяча миллиметровых кубиков, поставленных один на другой, даст столб в 1000 м = 1 км. А так как у нас кубиков еще в тысячу раз больше, то и составится 1000 км.

Рис. 100. Линейные размеры предмета так относятся к соответствующим размерам изображения, как расстояние предмета от объектива относится к глубине камеры
118. Из рис. 100 видно, что (вследствие равенства углов 1 и 2) линейные размеры предмета так относятся к соответствующим размерам изображения, как расстояние предмета от объектива относится к глубине камеры. В нашем случае, обозначив высоту самолета над землей в метрах через х, имеем пропорцию:
12000 : 8 = x : 0,12,
откуда х = 180 м.
119. Надо умножить 89,4 г на миллион, т. е. на тысячу тысяч.
Умножаем в два приема: 89,4 г X 1000 = 89,4 кг, потому что килограмм в тысячу раз больше грамма. Далее: 89,4 кг X 1000 = 89,4 тонны, потому что тонна в тысячу раз больше килограмма.
Итак, искомый вес - 89,4 тонны.
120. Всех путей по просекам от А до В можно насчитать 70. (Систематическое решение этой задачи возможно с помощью теории соединений, рассматриваемой в курсах алгебры.)
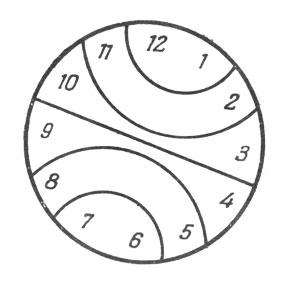
Рис. 101
121. Так как сумма всех чисел, обозначенная на циферблате, равна 78, то числа каждого из шести участков должны составлять вместе 78 : 6, т. е. 13. Это облегчает отыскание решения, которое показано на рис. 101.
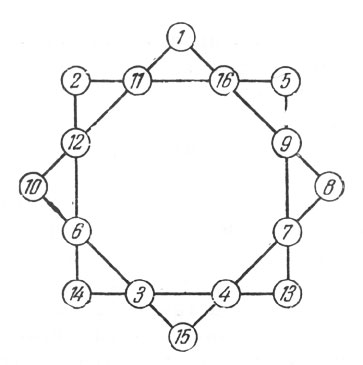
Рис. 102. Решение задачи 122
122-123. Решения показаны на прилагаемых рис. 102 и 103.
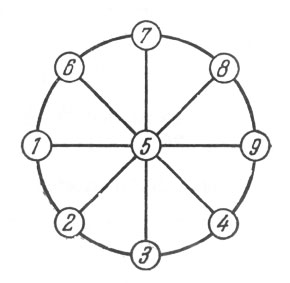
Рис. 103. Решение задачи 123
124. Трехногий стол всегда может касаться пола концами своих трех ножек, потому что через каждые три точки пространства может проходить плоскость и притом только одна; в этом причина того, что трехногий стол не качается. Как видите, она чисто геометрическая, а не физическая.
Вот почему так удобно пользоваться треногами для землемерных инструментов и фотографических аппаратов. Четвертая нога не сделала бы подставку устойчивее; напротив, пришлось бы тогда всякий раз заботиться о том, чтобы подставка не качалась.
125. На вопрос задачи легко ответить, если сообразить, какое время показывают стрелки. Стрелки в левом кружке (рис. 96) показывают, очевидно, 7 час. Значит, между концами этих стрелок заключена дуга в 5/12 полной окружности.
В градусной мере это составляет
360° х 5/12 = 150°.
Стрелки в правом кружке показывают, как нетрудно сообразить, 9 ч. 30 м. Дуга между их концами содержит 3 1/2 двенадцатых доли полной окружности или 7/24.
В градусной мере это составляет
360° х 7/24 = 105°.
l26. Принимая рост человека в 175 см и обозначив радиус Земли через R, имеем:
2 х 3,14 х(R + 175) - 2 х 3,14 х R = 2 x 3,14 x 175 = 1100 см,
т. е. около 11 м. Поразительно здесь то, что результат совершенно не зависит от радиуса шара и, следовательно, одинаков на исполинском Солнце и маленьком шарике.
127. Требованию задачи легко удовлетворить, если расставить людей в форме шестиугольника, как показано на рис. 104.

Рис. 104. Требованию задачи легко удовлетворить, если расставить людей в форме шестиугольника
128. Читатели, слыхавшие о неразрешимости задачи квадратуры круга, сочтут, вероятно, и предлагаемую задачу неразрешимой строго геометрически. Раз нельзя превратить в равновеликий квадрат полный круг, то - думают многие - нельзя превратить в прямоугольную фигуру и луночку, составленную двумя дугами окружности.
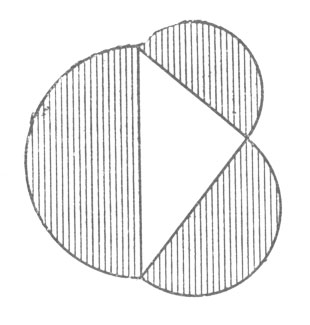
Рис. 105. Сумма площадей полукругов, построенных на катетах, равна полукругу, построенному на гипотенузе
Между тем, задача, безусловно, может быть решена геометрическим построением, если воспользоваться одним любопытным следствием общеизвестной Пифагоровой теоремы. Следствие, которое я имею в виду, гласит, что сумма площадей полукругов, построенных на катетах, равна полукругу, построенному на гипотенузе (рис. 105). Перекинув большой полукруг на другую сторону (рис. 106), видим, что обе заштрихованные луночки вместе равновелики треугольнику*. Если треугольник взять равнобедренный, то каждая луночка в отдельности будет равновелика половине этого треугольника (рис. 107).
* (Положение это известно в геометрии под названием "теоремы о гиппократовых луночках".)
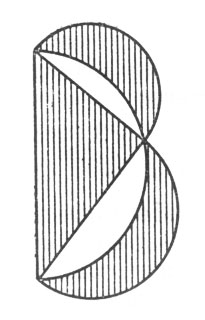
Рис. 106. Перекинув большой полукруг на другую сторону, видим, что обе заштрихованные луночки вместе равновелики треугольнику
Отсюда следует, что можно геометрически точно построить равнобедренный прямоугольный треугольник, площадь которого равна площади серпа.
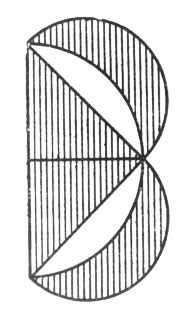
Рис. 107. Если треугольник взять равнобедренный, то каждая луночка в отдельности будет равновелика половине этого треугольника
А так как равнобедренный прямоугольный треугольник превращается в равновеликий квадрат (рис. 108), то и серп наш возможно чисто геометрическим построением заменить равновеликим квадратом.
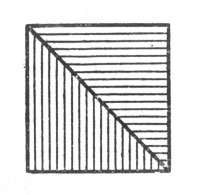
Рис. 108. Равнобедренный прямоугольный треугольник превращается в равновеликий квадрат
Остается только превратить этот квадрат в равновеликую фигуру Красного креста (составленную, как известно, из пяти примкнутых друг к другу равных квадратов).
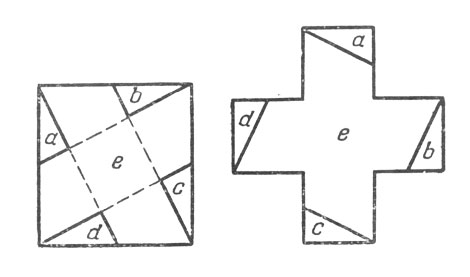
Рис. 109. Существует несколько способов выполнения такого построения
Существует несколько способов выполнения такого построения; два из них показаны на рис. 109 и 110; оба построения начинают с того, что соединяют вершины квадрата с серединами противоположных сторон.
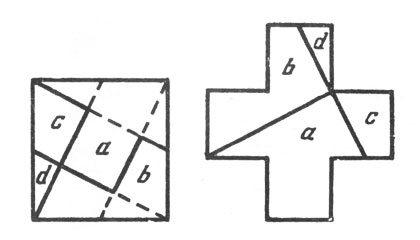
Рис. 110. Существует несколько способов выполнения такого построения
Важное замечание: превратить в равновеликий крест можно только такую фигуру серпа, которая составлена из двух дуг окружностей: наружного полукруга и внутренней четверти окружности соответственно большего радиуса*.
* (Тот лунный серп, который мы видим на небе, имеет несколько иную форму: его наружная дуга - полуокружность, внутренняя же - полуэллипс. Художники часто изображают лунный серп неверно, составляя его из дуг окружностей.)
Итак, вот ход построения креста, равновеликого серпу. Концы А и В серпа (рис. 111) соединяют прямой; в середине О этой прямой восставляют перпендикуляр и откладывают ОС = ОА. Равнобедренный треугольник ОАС дополняют до квадрата OADC, который превращают в крест одним из способов, указанных на рис. 109 и 110.
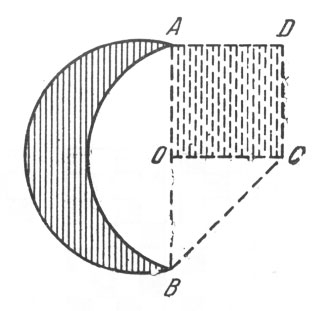
Рис. 111. Ход построения креста, равновеликого серпу
129. Указанная дополнительная возможность не облегчает задачу: все равно требуется шесть разрезающих плоскостей. В самом деле, внутренний кубик из числа тех 27, на которые надо разрезать большой куб, имеет шесть граней, и никакая разрезающая плоскость не может открыть сразу двух граней этого внутреннего кубика, как бы мы ни переставляли части.
130. Сначала посмотрим, каково может быть наименьшее число разрезов. Если мы провели один разрез, то доска распадается на две части. Следующим разрезом, если он рассечет обе из них, мы получим 4 части. Если мы расположим их так, что третий разрез пересечет их все, то число частей снова удвоится, и после третьего разреза мы получим 8 частей. После четвертого разреза мы получим самое большее 16 частей (если разрез пересечет все получившиеся ранее части), после пятого - 32 части. Значит после пяти разрезов мы никак еще не сможем получить 64 отдельных квадратика. И лишь после шестого разреза, когда число частей опять удвоится, мы можем рассчитывать получить 64 отдельных квадратика. Значит менее чем шестью разрезами обойтись невозможно.
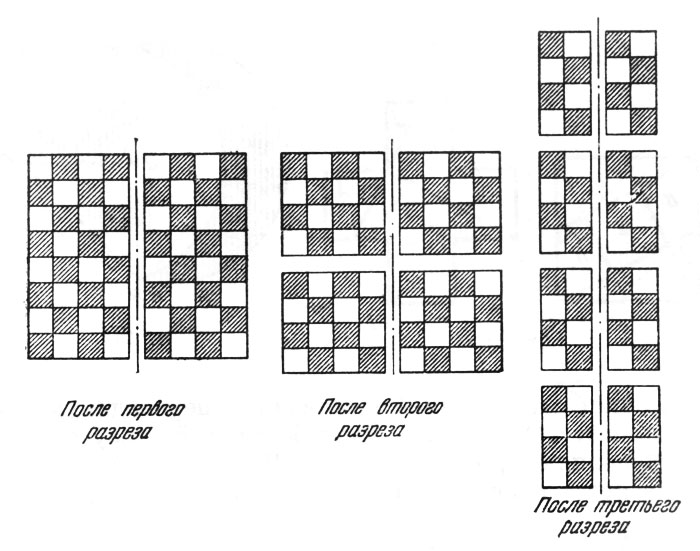
Рис. 112. Первые три разреза
Но теперь надо еще показать, что шесть разрезов можно в действительности осуществить так, чтобы каждый раз число частей удваивалось и в результате получилось 26 = 64 отдельных квадратика. Это уже нетрудно сделать: надо только следить, чтобы после каждого разреза все части оказывались равными и чтобы каждый очередной разрез разбивал каждую из частей пополам. На рис. 112 показаны первые три разреза.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'